LCSQ

Problem

A string $U$ is a common subsequences of strings $s$ and $t$ if the symbols of $u$ appear in order as a subsequence of both $s$ and $t$. For example "ACTG" is a common subsequence of "AACCTTGG" and "ACACTGTGA".

Analogously to the definition of longest common substring, $u$ is a longest common subsequence of $s$ and $t$ if there does not exist a longer common subsequence of the two strings. Continuing our above example, "ACCTTG" is a longest common subsequence of "AACCTTGG" and "ACACTGTGA" as is "AACTGG"

Given : Two DNA strings $s$ and $t$ (each having length at most 1kbp) in fasta format
Return : A longest commmon subsequence of $s$ and $t$. (if more than one solution exists, you may return any one.)

해설

간단하게 말해, 두개의 DNA sequence가 주어졌을 때, 이 DNA에서 연속되지 않더라도 공통된 subsequence를 구하라는 것이다. 위의 예시와 같이 AACCTTGG 와 ACACTGTGA에서 AA 와 ACA에서 비록 ACA사이에 C가 있지만 두 시퀀스의 AA는 공통 시퀀스가 된다. 이 문제는 longest common sequence라는 문제로 처음에는 greedy 하게 풀 수 있을 줄 알았다. 하지만 시도해 본 결과 풀 수 없었고, 인터넷에 물어보니 longest common sequence는 dynamic programming으로 풀어야 한다고 한다.

그렇다면 어떻게 dynamic programming 기법을 사용하여 이 문제를 해결해야 하는지가 문제이다. 이 문제는 두 시퀀스를 순회해 나가면서 공통 된 시퀀스를 만나면 길이를 추가해 나가는 것이 핵심이다. 간단하게 보자면 아래의 matrix를 구성해 문제를 해결 할 수 있다.

이 matrix는 두 DNA 시퀀스를 돌 수 있는 matrix로 시작은 (1,1)의 위치부터 시작한다.(가장 첫번째 인덱스는(0,0)) (1,1)에서 두 nt가 A, A로 일치한다. 그러므로 길이는 1이다. 여기서 (1,2)로 넘어가도 A, A가 나옴으로 AACCTTGG의 두번째 nt인 A부터 시작할 때 길이가 1이 된다. 하지만 (1, 3) 에서는 A, C로 다르다. 이때는 기존에 AA가 있음으로 길이는 유지되어 1이다. 그렇게 순회를 하다가 인덱스가 (3, 2)에서 A,A가 나오는데, 기존에 A, AC에서 길이가 1이었다가 AA, ACA로 만나 길이가 2가 됨으로 2를 적어준다.

이런 식으로 쭉 써보면 위와 같은 matrix를 만들 수 있게 된다. 그리고 두 시퀀스의 마지막 A,G가 있는 인덱스에서 가장 긴 길이가 6임을 알 수 있다. 이제 할 일은 마지막 글자부터 첫 글자까지 6글자의 common subsequence를 구하는 것이다.

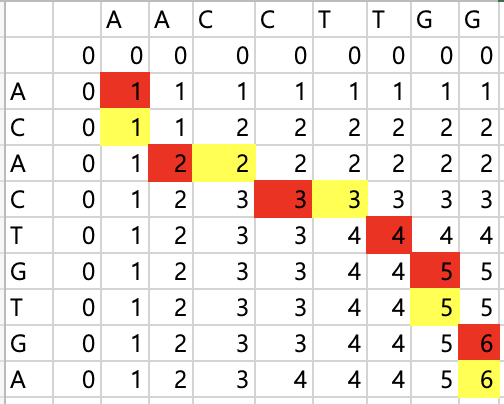
차례대로 돌아가보자. 방법은 같은 글자가 나오면 그 글자를 적고 대각선으로 올라가고, 만일 바로 위의 숫자가 왼쪽의 숫자보다 높을 경우 올라가고, 그렇지 않을 경우 왼쪽으로 가는 것이다. 먼저 AG는 같지 않은데 위가 높으니 위로 올라간다. GG가 나왔으니 G 를 적어준다.

G

대각선으로 한칸 올라갔으나 T와 G여서 다르다. 이때 위가 5여서 더 높으니 위로 올라간다. GG가 나왔다. 그러므로 G를 적어준다.

GG

이렇게 순서대로 적어주면서 올라가면

GGTCAA

그리고 거꾸로 해주면 AACTGG가 나와 정답을 맞출 수 있다. 정답 코드는 아래와 같다.

from Bio import SeqIO

def lcs(s1, s2):
    m = len(s1)
    n = len(s2)
    dp = [[0] * (n + 1) for _ in range(m + 1)]
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if s1[i - 1] == s2[j - 1]:
                dp[i][j] = dp[i - 1][j - 1] + 1
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
    lcs_len = dp[m][n]
    lcs_str = ''
    i, j = m, n
    while i > 0 and j > 0:
        if s1[i - 1] == s2[j - 1]:
            lcs_str = s1[i - 1] + lcs_str
            i -= 1
            j -= 1
        elif dp[i - 1][j] > dp[i][j - 1]:
            i -= 1
        else:
            j -= 1
    return lcs_str

seq_A, seq_B = [str(rec.seq) for rec in SeqIO.parse("rosalind_lcsq-3.txt", 'fasta')]
print(lcs(seq_A, seq_B))