Königsberg Bridges Problem

pDestiny·2021년 12월 12일

Network Science

목록 보기

1/10

제목을 읽을 수 없어 들어오시지 않았나요? Königsberg는 콰니히스베르크라고 읽습니다. 레온하르트 오일러가 7개의 다리의 문제를 풀고, 그래프 이론의 근간을 세운 곳이기도 합니다. 콰니히스베르크 7개의 다리 문제는 콰니히스베르크에 있는 Pregel River에 있는 두개의 큰섬(Kneiphof, Lomse)이 7개의 다리로 육상의 도시들과 연결되어 있습니다.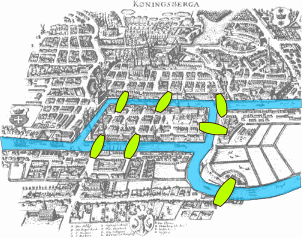
문제는 다리 전체를 다리 하나당 한번씩 지나는 방법을 찾는 것입니다. 방법이 존재할까요?

정답은 방법이 없다는 것입니다.

이건 한붓 그리기와 동일한 문제입니다. 어떤 도형을 주고, 이 도형을 한번도 손을때지 않고 그리는 문제는 언제가 한번 봤던 문제입니다. 문제를 어떻게 풀 수 있을까 여기저기 그려보고, 자신의 머리를 탓하기 일 수 이지만, 이 7개의 다리 문제에서 오일러는 다른 관점을 제시합니다. 한 붓 그리기 문제는 기술의 문제가 아니라 그 구조가 가지고 있는 특성때문에 풀 수 없다는 것입니다. 이제는 문제를 못푸는 머리를 탓할 필요 없이 한 붓으로 그려지지 않는 도형을 탓할 수 있게되었습니다!

오일러는 7개의 다리 문제를 그래프 구조로 다시 해석합니다.

동그라미가 섬과 내지를 의미하고(node 혹은 vertex) 다리가 간선(edge 혹은 link)를 의미합니다. 오일러는 노드가 가지고 있는 edge의 개수에 주목을 하여 문제를 해결합니다.

한붓 그리기가 가능한 조건은 아래와 같습니다.

간선 개수가 홀수개인 시작지점과 종료지점 노드가 필요
나머지 노드들은 간선의 개수가 짝수

위의 그래프의 노드의 간선 개수를 세보죠.

A : 3개
B : 5개
C : 3개
D : 3개

간선의 개수가 홀수개인 노드가 2개를 초과함으로, 모든 edge를 한번만 통과하는 것은 불가능하다는 것을 알수가 있습니다. 문제를 해결 수 있게 만들려면 A-B, B-C 간선중 하나씩, 총 2개를 지우면 됩니다.

A : 2개
B : 3개
C : 2개
D : 3개

이제 조건에 맞게 되었으니 B 또는 D에서 시작한다면 문제를 해결 할 수 있습니다.

B -> C -> D -> A -> B -> D

총 5개의 간선이 있고 5개의 간선를 딱 한번씩 거치는 것이 가능해졌습니다. 하지만 혹시 이 문제에만 국한된 원칙이 아닐까요? 다른 문제들도 살펴보겠습니다.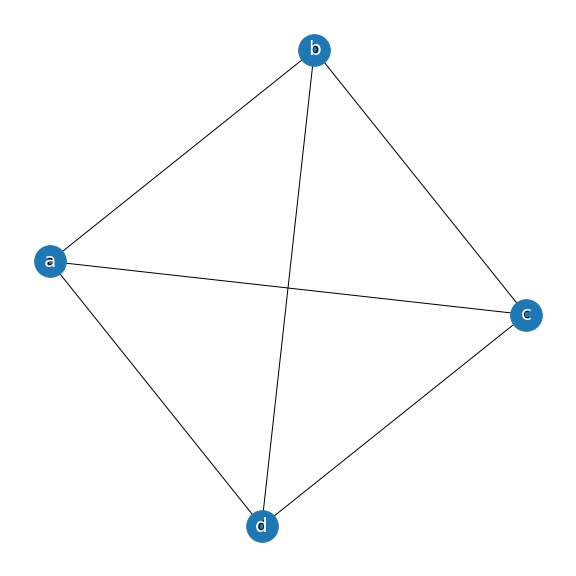

위의 그래프의 노드별 간선의 개수를 세보죠.

A : 3개
B : 3개
C : 3개
D : 3개

이 그래프는 각 노드가 자신을 제외한 모든 노드에 연결되어 있는 Complete Graph 이기 때문에 당연하게도 각각의 노드는 $4 - 1 = 3$ 개의 노드를 각각 가지고 있습니다. 이 문제도 7개 다리 문제와 동일한 구조적 문제를 가지고 있습니다. 간선의 개수가 홀수 인 노드가 2개를 초과했기 때문에 이 문제 역시 한붓으로 그릴 수 있는 방법은 없습니다.

여기까지는 여러가지 그래프의 한붓그리기가 데이터의 구조적인 이유로 문제 해결책의 존재여부가 결정되는 것을 설명하였습니다. 더 복잡한 그래프가 존재하더라도, 노드별 엣지의 개수만 알 수 있다면 우리는 문제를 해결 할 수 있는지 알 수 있습니다.

하지만 여기까지는 어디까지나 가능 여부만을 판단할 수 있는 기준이었습니다. 실제로는 어마어마하게 많은 노드와 간선이 존재할 수 있으므로, 거대한 그래프에서 한붓 그리기는 조금더 생각을 해보아야 합니다.

그래프에서 모든 edge를 단 한번만 거치는 path를 Eulerian Path라고 합니다. 이제 이 Eulerian Path를 구현하는 방법에 대해 알아보겠습니다.

Eulerian Path

(undirected graph의 경우)한붓 그리기 알고리즘은 아래의 순서를 따릅니다.

빈 Stack 하나와 Eulerian Path가 들어갈 리스트(EP)를 준비합니다.
1. 만일 주어진 그래프에서 모든 노드의 degree가 짝수라면 어떤 것을 골라도 상관 없습니다.
2. 만일 그래프에서 딱 2개만 degree가 홀수인 노드가 있다면 그 둘 중 하나를 고릅니다.
3. 1,2 에 속하지 않는 그래프라면 Eulerian Path는 존재하지 않습니다.
만일 현재 노드에 degree가 0이면 EP에 추가하고 Stack에서 노드 하나를 제거하고 제거된 노드를 현재 노드로 만듭니다. 만일 degree가 0이 아니면 Stack에 노드를 추가하고 그 노드의 neighbor중 아무 것이나 취하고, 현재 노드와 선택된 이웃 사이의 edge를 삭제합니다. 그리고 선택된 이웃 노드를 현재 노드로 만듭니다.
스탭 2를 현재 노드의 이웃이 존재하지 않고 Stack이 빌때까지 반복합니다.

아래와 같은 그래프가 있을때, 제일 처음 해야 할 것은 그래프에 Eulerian Path가 존재하는 가를 확인해야 합니다.

Degree 개수 (1): 4개, (2): 4개, (3): 2개, (4): 2개, (5): 2개, (6): 2개, (7): 2개, (8): 4개, (9): 2개

degree 개수가 모든 노드에서 짝수개임으로 Eulerain Path가 존재하는 것을 확인 했습니다. 이제 할일은 이 중에서 아무 노드를 현재 노드로 만들고 알고리즘을 시작하는 것입니다. 먼저 1번 노드부터 시작하겠습니다.

Stack : []
현재 노드 : 1
EP : []

먼저 1번 노드의 degree가 0이 아님으로 이웃중 아무나 하나를 고릅니다. 2를 고르겠습니다. 그리고 1을 Stack에 집어 넣고 1과 2사이의 엣지를 삭제합니다. 이제는 2가 현재 노드가 되었습니다.

Stack : [1]
현재 노드 : 2
EP : []

이번에는 2번노드의 이웃을 에서 하나를 고릅니다. 3번을 고르겠습니다. 그런다음 2를 Stack에 집어 넣고 2번과 3번 사이의 엣지를 삭제합니다. 이제는 3번 노드가 현재 노드가 되었습니다.

Stack : [1, 2]
현재 노드 : 3
EP : []

이번에는 3번노드의 이웃을 에서 하나를 고릅니다. 4번을 고르겠습니다. 그런다음 3를 Stack에 집어 넣고 3번과 4번 사이의 엣지를 삭제합니다. 이제는 4번 노드가 현재 노드가 되었습니다.

Stack : [1, 2, 3]
현재 노드 : 4
EP : []

이번에는 4번노드의 이웃을 에서 하나를 고릅니다. 2번밖에 남지 않았음으로 2번을 선택합니다. 그런다음 4를 Stack에 집어 넣고 4번과 2번 사이의 엣지를 삭제합니다. 이제는 2번 노드가 현재 노드가 되었습니다.

Stack : [1, 2, 3, 4]
현재 노드 : 2
EP : []

이번에는 2번노드의 이웃을 에서 하나를 고릅니다. 8번밖에 남지 않았음으로 8번을 선택합니다. 그런다음 2를 Stack에 집어 넣고 2번과 8번 사이의 엣지를 삭제합니다. 이제는 8번 노드가 현재 노드가 되었습니다.

Stack : [1, 2, 3, 4, 2]
현재 노드 : 8
EP : []

이번에는 8번노드의 이웃을 에서 하나를 고릅니다. 1번을 고르겠습니다. 그런다음 8를 Stack에 집어 넣고 8번과 1번 사이의 엣지를 삭제합니다. 이제는 1번 노드가 현재 노드가 되었습니다.

Stack : [1, 2, 3, 4, 2, 8]
현재 노드 : 1
EP : []

이번에는 1번노드의 이웃을 에서 하나를 고릅니다. 6번을 고르겠습니다. 그런다음 1를 Stack에 집어 넣고 1번과 6번 사이의 엣지를 삭제합니다. 이제는 6번 노드가 현재 노드가 되었습니다.

Stack : [1, 2, 3, 4, 2, 8, 1]
현재 노드 : 6
EP : []

이번에는 6번노드의 이웃을 에서 하나를 고릅니다. 9번을 고르겠습니다. 그런다음 6를 Stack에 집어 넣고 6번과 9번 사이의 엣지를 삭제합니다. 이제는 9번 노드가 현재 노드가 되었습니다.

Stack : [1, 2, 3, 4, 2, 8, 1, 6]
현재 노드 : 9
EP : []

이번에는 9번노드의 이웃을 에서 하나를 고릅니다. 1번을 고르겠습니다. 그런다음 9를 Stack에 집어 넣고 9번과 1번 사이의 엣지를 삭제합니다. 이제는 1번 노드가 현재 노드가 되었습니다.

Stack : [1, 2, 3, 4, 2, 8, 1, 6, 9]
현재 노드 : 1
EP : []

현재 1번 노드는 degree가 0입니다. 그러므로 1번 노드를 EP에 집어 넣고, Stack에서 한개를 빼와 현재 노드로 만듭니다. 현재 노드는 9이 됩니다.

Stack : [1, 2, 3, 4, 2, 8, 1, 6]
현재 노드 : 9
EP : [1]

현재 9번 노드는 degree가 0입니다. 그러므로 9번 노드를 EP에 집어 넣고, Stack에서 한개를 빼와 현재 노드로 만듭니다. 현재 노드는 6이 됩니다.

Stack : [1, 2, 3, 4, 2, 8, 1]
현재 노드 : 6
EP : [1, 9]

현재 6번 노드는 degree가 0입니다. 그러므로 6번 노드를 EP에 집어 넣고, Stack에서 한개를 빼와 현재 노드로 만듭니다. 현재 노드는 1이 됩니다.

Stack : [1, 2, 3, 4, 2, 8]
현재 노드 : 1
EP : [1, 9, 6]

현재 1번 노드는 degree가 0입니다. 그러므로 1번 노드를 EP에 집어 넣고, Stack에서 한개를 빼와 현재 노드로 만듭니다. 현재 노드는 8이 됩니다.

Stack : [1, 2, 3, 4, 2]
현재 노드 : 8
EP : [1, 9, 6, 1]

이번에는 8번노드의 이웃을 에서 하나를 고릅니다. 5번을 고르겠습니다. 그런다음 8를 Stack에 집어 넣고 8번과 5번 사이의 엣지를 삭제합니다. 이제는 5번 노드가 현재 노드가 되었습니다.

Stack : [1, 2, 3, 4, 2, 8]
현재 노드 : 5
EP : [1, 9, 6, 1]

이번에는 5번노드의 이웃을 에서 하나를 고릅니다. 7번을 고르겠습니다. 그런다음 5를 Stack에 집어 넣고 5번과 7번 사이의 엣지를 삭제합니다. 이제는 7번 노드가 현재 노드가 되었습니다.

Stack : [1, 2, 3, 4, 2, 8, 5]
현재 노드 : 7
EP : [1, 9, 6, 1]

이번에는 7번노드의 이웃을 에서 하나를 고릅니다. 8번을 고르겠습니다. 그런다음 7를 Stack에 집어 넣고 7번과 8번 사이의 엣지를 삭제합니다. 이제는 8번 노드가 현재 노드가 되었습니다.

Stack : [1, 2, 3, 4, 2, 8, 5, 7]
현재 노드 : 8
EP : [1, 9, 6, 1]

현재 8번 노드는 degree가 0입니다. 그러므로 8번 노드를 EP에 집어 넣고, Stack에서 한개를 빼와 현재 노드로 만듭니다. 현재 노드는 7이 됩니다.

Stack : [1, 2, 3, 4, 2, 8, 5]
현재 노드 : 7
EP : [1, 9, 6, 1, 8]

현재 7번 노드는 degree가 0입니다. 그러므로 7번 노드를 EP에 집어 넣고, Stack에서 한개를 빼와 현재 노드로 만듭니다. 현재 노드는 5이 됩니다.

Stack : [1, 2, 3, 4, 2, 8]
현재 노드 : 5
EP : [1, 9, 6, 1, 8, 7]

현재 5번 노드는 degree가 0입니다. 그러므로 5번 노드를 EP에 집어 넣고, Stack에서 한개를 빼와 현재 노드로 만듭니다. 현재 노드는 8이 됩니다.

Stack : [1, 2, 3, 4, 2]
현재 노드 : 8
EP : [1, 9, 6, 1, 8, 7, 5]

현재 8번 노드는 degree가 0입니다. 그러므로 8번 노드를 EP에 집어 넣고, Stack에서 한개를 빼와 현재 노드로 만듭니다. 현재 노드는 2이 됩니다.

Stack : [1, 2, 3, 4]
현재 노드 : 2
EP : [1, 9, 6, 1, 8, 7, 5, 8]

현재 2번 노드는 degree가 0입니다. 그러므로 2번 노드를 EP에 집어 넣고, Stack에서 한개를 빼와 현재 노드로 만듭니다. 현재 노드는 4이 됩니다.

Stack : [1, 2, 3]
현재 노드 : 4
EP : [1, 9, 6, 1, 8, 7, 5, 8, 2]

현재 4번 노드는 degree가 0입니다. 그러므로 4번 노드를 EP에 집어 넣고, Stack에서 한개를 빼와 현재 노드로 만듭니다. 현재 노드는 3이 됩니다.

Stack : [1, 2]
현재 노드 : 3
EP : [1, 9, 6, 1, 8, 7, 5, 8, 2, 4]

현재 3번 노드는 degree가 0입니다. 그러므로 3번 노드를 EP에 집어 넣고, Stack에서 한개를 빼와 현재 노드로 만듭니다. 현재 노드는 2이 됩니다.

Stack : [1]
현재 노드 : 2
EP : [1, 9, 6, 1, 8, 7, 5, 8, 2, 4, 3]

현재 2번 노드는 degree가 0입니다. 그러므로 2번 노드를 EP에 집어 넣고, Stack에서 한개를 빼와 현재 노드로 만듭니다. 현재 노드는 1이 됩니다.

Stack : []
현재 노드 : 1
EP : [1, 9, 6, 1, 8, 7, 5, 8, 2, 4, 3, 2]

스택은 비었고, 현재 노드 1은 더이상 이웃이 없음으로 더이상의 진행은 없습니다. EP가 바로 우리가 원하는 Eulerian Path가 됩니다. 따라오느라 고생하셨습니다.

Stack : []
현재 노드 : 1
EP : [1, 9, 6, 1, 8, 7, 5, 8, 2, 4, 3, 2, 1]

Implementation

import networkx as nx
import toolz as tz
from toolz.curried import *
import matplotlib.pyplot as plt
import random

g = nx.Graph()

g.add_edges_from([
    (9,1),
    (6,1),
    (9,6),
    (2,1),
    (1,8),
    (2,4),
    (4,3),
    (3,2),
    (2,8),
    (5,7),
    (5,8),
    (7,8)
])

even = lambda x: x % 2 == 0

def get_eulerian_path(g):
    
    g = g.copy()
    degrees = [val for node, val in g.degree()]
    
    if not all(map(even, degrees)) and count(filter(complement(even), degrees)) != 2:
        print("No Euclerian Path exists.")
        return False
    
    else:
        stack = []
        ep = []
        
        if all(map(even, degrees)):
            cur_node = random.choice(list(map(first, g.degree())))
        else:
            cur_node = random.choice(list(map(first, filter(compose(complement(even), last), g.degree()))))
    
        # algorihtm start
        while len(stack) !=0 or g.degree[cur_node] != 0:
            neighbors = list(g.neighbors(cur_node))
            
            if len(neighbors) != 0:
                prev_node = cur_node
                cur_node = random.choice(neighbors)
                stack.append(prev_node)
                g.remove_edge(prev_node, cur_node)
            
            else:
                ep.append(cur_node)
                cur_node = stack.pop()
        
        ep.append(cur_node)
        
        return ep, g

이 코드를 실행하면 Eulerain Path 를 얻을 수 있습니다. 그리고 다시 연결해 보면 아래 그림과 같이 다시 연결되는 것을 보실 수 있습니다.

pDestiny

Bioinformatician

다음 포스트

Königsberg Bridges Problem

Network Science

Eulerian Path

Implementation

Dijkstra Algorithm

0개의 댓글