https://book.naver.com/bookdb/book_detail.nhn?bid=16268369
으뜸 파이썬과 함께 공부하는 포스트입니다.
곱집합
집합론에서는 곱집합 혹은 데카르트 곱이라는 개념이 있다. 이것은 각 집합에서 임의의 원소를 가져와 만들 수 있는 조합을 하나의 튜플로 표현한다. 그리고 가능한 모든 튜플을 항목으로 하는 튜플의 집합이다.
이 두 집합의 곱집합은 A * B로 표현하며, 그 원소는 { (a, b) | a ∈ A, b ∈ B} 와 같이 집합 A의 임의의 원소 a와 집합 B의 임의의 원소 a와 집합 B의 임의의 원소 b를 이용해 만들 수 있는 모든 튜플 (a,b)의 집합이 된다.
두 집합이 주어졌을 때 집합의 곱집합을 구하는 함수는 다음 코드와 같이 구할 수 있다. 이 코드에는 하나의 함수가 나타난다. 이 함수는 두개의 집합을 인자로 바아 결과를 반환하는 하나의 행으로 구성되어 있다. 이 함수를 호출하면 집합을 반환한다.
이 집합에는 (i, j) 라는 두개의 요소를 가진 튜플들이 채워지게 되며, i와 j는 인자로 주어진 집합 set1과 set2에서 하나씩 얻어온다. 따라서 이 함수는 두 집합의 요소를 하나씩 취해 만들 수 있는 모든 튜플을 생성하여 이를 원소로 하는 집합을 생성하여 반환한다. 이것은 두 집합의 곱집합이 된다.
이 함수를 이용하여 두 집합의 곱집합을 구해보자.

실행 결과
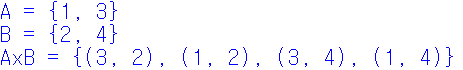
LAB 6-11 곱집합 연산
-
다음 두 집합이 있을 경우 product_set() 함수를 이용하여 두 집합의 곱집합을 구하여라.
A = {1, 2} B = {'A', 'B', 'C'}

1) A * B

2) B * A

3) A * A

4) B * B

이제 거듭제곱 연산을 알아보자. 집합의 거듭제곱은 이러한 곱집합을 여러번 시행하는 것이다.
위의 원소를 2개 가진 A는 3번의 거듭제곱을 통해 2^3 = 8개의 튜플을 요소로 갖는 집합이 됨을 알 수 있다. 그리고 각각의 거듭제곱마다 튜플이 원소로 생성되고, 이 튜플이 다른 집합과 곱집합을 생성하므로 중첩된 튜플 구조로 표현된다.
또, 아래에서 정의한 exp() 함수로 set에 대한 거듭제곱을 수행 할 수 있다. 이 때 집합 A의 세제곱은 A A A 이므로 product_set() 함수를 2회 호출하면 된다.

실행 결과

집합과 리스트의 가장 큰 차이는 집합은 중복된 원소가 없다는 것이다. 주사위를 던져서 얻는 경우의 수를 예로 들어보자. 두번 던져서 얻는 모든 경우를 나열하면 각 원소는 주사위 눈을 의미하는 값의 튜플로 나타낼 수 있다. 이 두 눈의 합을 구하려면 튜플의 원소 합을 구하는 sum(tuple)을 사용한다.
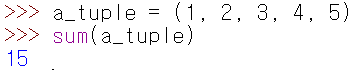
이제 앞에서 언급한 주사위를 두 번 던져서 나오는 모든 경우에 대해 눈의 합을 구해보자.

실행 결과

위 코드를 보면 주사위의 가장 작은 눈 1의 두개 합이 2이고, 가장 큰 눈의 합 6과 6은 12가 된다. 다른 합은 몇가지 서로 다른 방식으로 나올 수 있지만, 집합은 중복을 허용하지 않기 때문에 나올 수 있는 수는 2에서 12까지 11가지이다.
그러나 각각의 경우에 눈의 합을 구하여 sum_list 리스트에 넣으면 결과가 다르다.
리스트는 중복을 허용하기 때문에 6 * 6 = 36가지 출력 결과 모두 나온다.
두번이 아니라 주사위를 세번 던지면 튜플 안에 또 튜플이 들어가는 중첩 튜플이 생긴다. (a,(b,c))의 형태인데, 이런 튜플은 단순히 sum() 함수로 원소의 합을 구할 수 없다. 그렇게 할 경우
TypeError: unsupported operand type(s) for +: 'int' and 'tuple' 에러가 발생한다.
이런 중첩튜플은 재귀호출을 통해 튜플 합을 구할 수 있다. 이 때 사용되는 함수는 튜플의 항목이 튜플일 경우 다시 자기 자신을 호출한다.
이런 방식으로 마지막 부동소수점이나 정수를 처리하는 단계까지 가게 되면 해당 값을 반환한다. 한번 시도해보자.

실행 결과

isinstance는 어떤 항목 tup가 정수형인지를 알아보기 위한 함수이다. 이것이 참이면 tup을 반환, 아니면 tup의 모든 원소를 순환하며 이 원소의 합을 구하는 코드가 아래 코드의 핵심이다.
zip() 함수를 이용한 집적화
지금까지 배운 리스트, 딕셔너리, 집합, 튜플같은 자료형을 반복가능 자료형이라 한다. 이런 반복가능 자료형 여러개를 넘겨주면 이들을 합쳐서 튜플 반복자를 반환하는 함수가 zip() 함수이다. 이것을 여러개 하는 것이 집적화라고 한다.
zip(*iterables)인자가 전달되지 않으면 zip() 함수는 공백 반복자를 반환한다. 반복가능 자료형이 하나 들어오면 zip() 함수는 튜플형 반복가능 자료형을 반환한다. 이 튜플의 각 원소는 인자로 넘어온 데이터에서 얻어진 값 하나씩이 전달된다.
다수의 반복가능 자료형 인자 n개가 들어오면 튜플 반복자는 인자의 수인 n개 만큼의 튜플을 원소로 가진 튜플 반복자가 된다. 이 때 i번째 원소인 튜플은 인자로 넘어온 각 반복가능 자료형 인자의 i번째 원소들로 구성된다. 이제 실습을 해보자.

이 코드를 수정하여 a = [10, 20, 30], b = ('ten', 'twenty', 'thirty')의 리스트와 튜플을 zip()함수에 넣어보자

zip() 함수가 반환하는 것은 zip 객체인데 이는 반복이 가능하므로 for문으로 출력 가능하다.

zip() 함수에 하나의 반복가능 자료형 인자를 전달한 경우이다. 중괄호 내부에 튜플이 하나씩 만들어진다.
그런데 생성되는 요소가 튜플이기 때문에 내부에는 'a'가 아니라 ('a',), 즉, 쉼표가 들어가므로 주의해야 한다.
이제 여러개의 반복가능 자료형 인자를 전달한 경우를 보자.
각 인자들이 가진 요소의 개수가 모두 다르다. 그러므로 생성되는 튜플의 개수를 잘 살펴보자.

세 종류의 자료형 데이터 중 요소가 가장 적은 것은 3개가 있는 int_tuple이다. 그래서 세가지를 zip() 함수로 묶으면 가장 작은 수에 맞춰 3개의 튜플이 생성된다.
zip() 함수로 묶인 튜플들을 원래의 반복가능 자료로 되돌리기도 가능하다. 다른 함수를 쓰는게 아니라 zip() 함수에 묶은 자료를 인자로 입력하고 * 연산자를 인자 앞에 붙여서 수행한다.

튜플과 스트링의 슬라이싱
튜플과 스트링의 슬라이싱도 리스트와 동일한 방식을 사용한다.

튜플의 슬라이싱도 리스트와 마찬가지로 인덱스를 사용 가능하고, 음수 인덱스도 가능하다.
슬라이싱은 리스트 뿐만 아니라 문자열에도 적용 가능하다.


