[백준] 1004 - 어린왕자 (java)

너무 오랫동안 알고리즘 문제를 안 풀어서, 자바를 사용안해서 머리를 다시 굴려볼 겸 문제 하나를 풀어보고 정리했다.

[백준] 1004 - 어린왕자 링크

문제 요약

• 출발점, 도착점 에 대한 좌표가 존재한다.
• 특정 좌표와 반지름을 가지는 행성(원)이 여러개 존재한다.
• 출발점에서 도착점까지 행성을 최대한 거치지 않을 것인데 이 때 거치는 행성의 수를 구해라

주어지는 제한 사항은 딱히 고려하지 않아도 될 정도로 적다.

요구사항 생각하기

출발점에서 도착점까지 알아서 최적화 해서 간다

하트를 그리면서 가던 직진하던 알아서 행성을 거치지 않을 수 있다면 거치지 않고 가기 때문에 신경쓸 필요없다.

행성을 '거치다' 라는 것은

지점과 관련이 있기 때문에(포함되어있기 때문에) 행성을 지나간다고 볼 수 있다.

출발점이 특정 행성 범위에 포함되고 도착점은 해당 행성에 포함되지 않는다면 지나가야 한다.

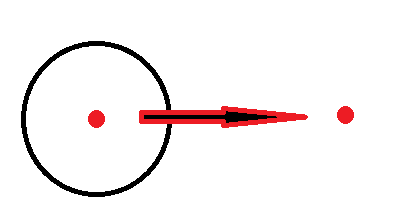
출발점이 특정 행성 범위에 포함되지 않지만 도착점은 포함되는 경우 지나가야 한다.

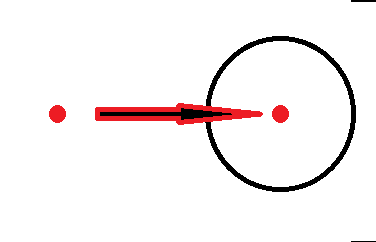
출발점과 도착점 모두 포함하지 않는 행성은 도출해야하는 결론과 관계 없다.

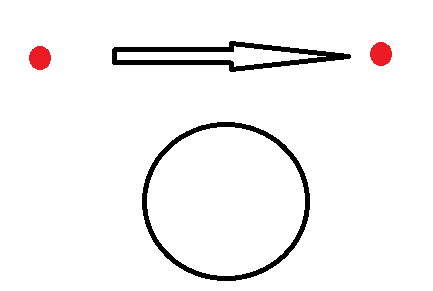
출발점과 도착점 모두 포함하는 행성은 도출해야하는 결론과 관계 없다.

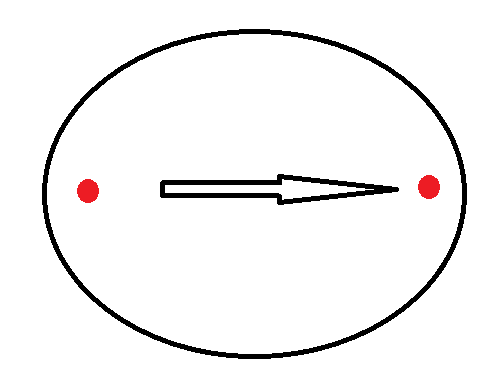
결론적으로 구해야 하는 것

출발점을 포함하지만 도착점은 포함하지 않는 행성의 개수와

도착점을 포함하지만 출발점은 포함하지 않는 행성의 개수를 더하면 된다.

결론을 위해 필요한 것

원(행성)이 점(시작점 또는 도착점)을 포함하고 있는지를 계산해야 한다.

행성의 반지름이 주어지기 때문에 삐따고라스 공식을 사용해서 [원의 중심과 점 간의 거리]가 [반지름]과 같거나 작다면 행성 안에 점이 포함되어있다고 할 수 있다.

문제에서 겹치는 경우는 주어지지 않기 때문에 작은 경우만 생각해도 될 것 같다.

요구 사항 정리

1. 매 케이스마다 주어지는 시작점, 도착점, 행성 목록을 얻는다.

2. 행성 목록을 순회하며 시작점 또는 도착점 하나만 포함된 경우의 수(XOR)를 구한다.

풀이 코드

package 백준.math;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;

public class boj1004_어린왕자 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder stringBuilder = new StringBuilder();
        int caseNum = Integer.parseInt(br.readLine());
        // one of case phase 
        for (int i = 0; i < caseNum; i++) {
            int[] pointArr = getIntArrFromStr(br.readLine());
            Point startPoint = new Point(pointArr[0], pointArr[1]);
            Point endPoint = new Point(pointArr[2], pointArr[3]);
            int planetNum = Integer.parseInt(br.readLine());
            int overlapNum = 0;
            // planet list for one phase
            for (int j = 0; j < planetNum; j++) {
                int[] planetArr = getIntArrFromStr(br.readLine());
                Planet planet = new Planet(planetArr[0], planetArr[1], planetArr[2]);
                if (isPointInPlanet(startPoint, planet) ^ isPointInPlanet(endPoint, planet)) {
                    overlapNum++;
                }
            }
            stringBuilder.append(overlapNum).append("\n");
        }
        System.out.println(stringBuilder);
    }

    static class Point {
        int x;
        int y;

        public Point(int x, int y) {
            this.x = x;
            this.y = y;
        }
    }

    static class Planet {
        int radius;
        Point point;

        public Planet(int x, int y, int radius) {
            this.radius = radius;
            this.point = new Point(x, y);
        }
    }

    static int[] getIntArrFromStr(String str) {
        return Arrays.stream(str.split(" ")).mapToInt(Integer::parseInt).toArray();
    }

    static boolean isPointInPlanet(Point point, Planet planet) {
        Point planetPoint = planet.point;
        double distance = Math.sqrt(Math.pow(planetPoint.x - point.x, 2) + Math.pow(planetPoint.y - point.y, 2));
        return distance <= planet.radius;
    }
}

나머지 부분들은 클래스를 만들고 초기화 해서 계산에 사용되는 것 뿐이고

2중 for문 내부를 유심히 보면 될 것 같다.

    static boolean isPointInPlanet(Point point, Planet planet) {
        Point planetPoint = planet.point;
        double distance = Math.sqrt(Math.pow(planetPoint.x - point.x, 2) + Math.pow(planetPoint.y - point.y, 2));
        return distance <= planet.radius;
    }

해당 메소드를 통해 Point하나가 Planet에 포함되었는지 여부를 삐따고라스 공식으로 구한다.

if (isPointInPlanet(startPoint, planet) ^ isPointInPlanet(endPoint, planet)) {
   overlapNum++;
}

배타적 논리합을 이용해 true 일 경우 지나쳐야 하는 행성 수를 업데이트 한다.