문제
도현이는 우주의 신이다. 이제 도현이는 아무렇게나 널브러져 있는 n개의 별들을 이어서 별자리를 하나 만들 것이다. 별자리의 조건은 다음과 같다.
- 별자리를 이루는 선은 서로 다른 두 별을 일직선으로 이은 형태이다.
- 모든 별들은 별자리 위의 선을 통해 서로 직/간접적으로 이어져 있어야 한다.
별들이 2차원 평면 위에 놓여 있다. 선을 하나 이을 때마다 두 별 사이의 거리만큼의 비용이 든다고 할 때, 별자리를 만드는 최소 비용을 구하시오.
문제 요약
2차원 좌표를 여러개 주는데 최소한의 비용으로 모두 이어야 한다.
풀이 과정
존재하는 모든 노드들을 최소한의 비용으로 모두 연결해야 하는 최소 신장 트리 문제이다.
단 노드와 노드간 거리가 직접 수치로 주어지는 것이 아니라
노드 하나에 대한 2차원 좌표가 주어지기 때문에 거리를 직접 구해야 한다.
어떤 순서로 특정 노드와 다른 노드를 연결해가며 최소 거리를 만들 것인지를 잘 생각해야 한다고 보았다.
(0,0) 기준 가까운 순서대로?
어떤 노드부터 시작해야하는지가 없기 때문에 기준을 구해서 그 순서대로 연결해나가면 어떨까 먼저 생각해보았다.
하지만 바보같은 생각이라는 것을 금방 깨달았다.
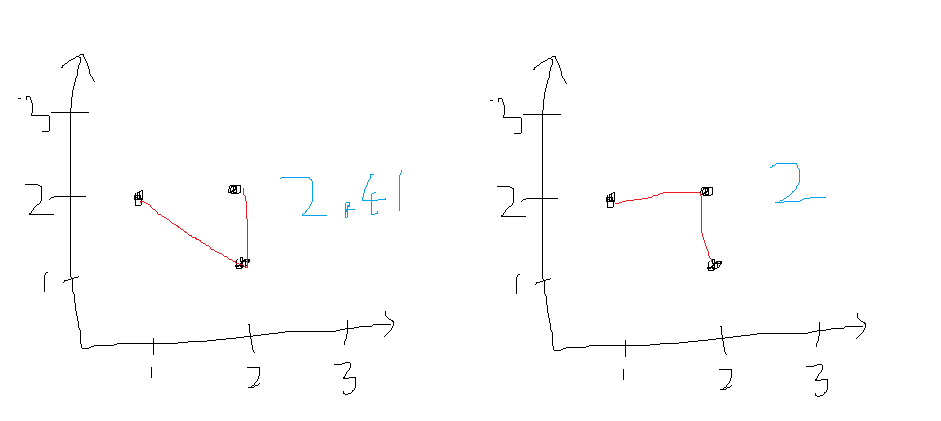
모든 노드간 거리 구하기
노드 수가 최대 100개밖에 안되기 때문에 충분하고, 이 방법 밖에 없는 것 같다.
시작 지점이 정해져있다면 모를까 모든 노드들 간 간선의 거리를 구해보고 가장 작은 것 부터 그려나가야 할 것 같다.
우선 별 객체를 만들어 노드 번호를 매기고 좌표를 만들어주고
class Star {
int id;
double x;
double y;
}간선 객체를 만들어 두 별 간 거리와 번호를 매긴다.
class StarEdge {
int start;
int end;
double dist;
}모든 별들에 대한 간선을 배열에 저장하고 거리 오름차순으로 정렬해 최소거리로 연결해나가면 된다.
한 번 특정 노드번호가 최소거리로 연결되었다면 이후에 추가적으로 연결될 필요 없다.
즉 사이클을 돌면 안된다.
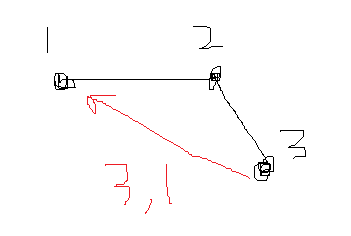
1-2-3은 이미 최소거리로 연결되어있으며 StarEdge(x: 3, y: 1,거리: ??)는 더 이상 연결될 필요 없다.
이를 판단하기 위해서는 특정 규칙으로 노드들이 연결될 때 마다 근본(부모) 노드를 동일하게 초기화 해주고,
특정 간선의 근본 노드가 같으면 연결하지 않으면 된다.
이를 구현하기 위해 union-find를 사용하면 된다.
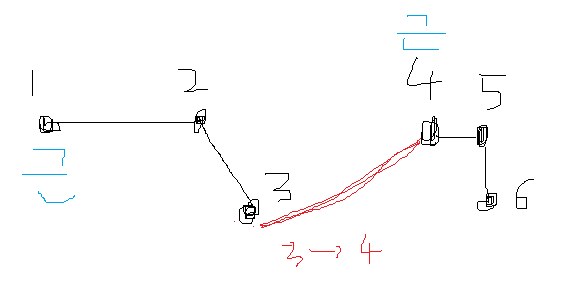
이렇게 근본이 다르면 연결될 수 있다.
무지성으로 그림판에 그렸는데 최소 거리부터 연결해나가니 위와 같은 경우라면
4-5
5-6
2-3
1-2
3-4와 같은 순서로 연결되었을 것이다.
[1-2],[2-3],[3-4] 보다 [4-6]이 짧은데요? 라고 생각할 수 있지만 위에서 설명한 것 처럼 4번과 6번은 이미 최소거리로 갱신[4-5, 5-6]하며 같은 근본이 되었기 때문에 연결과정에서 스킵되는 것입니다!
풀이 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class boj4386_별자리_만들기 {
static int[] parents;
public static void main(String[] args) throws IOException {
BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
int len = Integer.parseInt(bufferedReader.readLine());
parents = new int[len];
Star[] starArr = new Star[len];
for (int i = 0; i < len; i++) {
double[] starInfo = Arrays.stream(bufferedReader.readLine().split(" ")).mapToDouble(Double::parseDouble).toArray();
Star star = new Star(i, starInfo[0], starInfo[1]);
starArr[i] = star;
parents[i] = i;
}
List<StarEdge> edgeList = new ArrayList<>();
for (int i = 0; i < starArr.length - 1; i++) {
for (int j = i + 1; j < starArr.length; j++) {
double dist = calDist(starArr[i].x, starArr[j].x, starArr[i].y, starArr[j].y);
edgeList.add(new StarEdge(starArr[i].id, starArr[j].id, dist));
}
}
double answer = 0.0;
int cnt = 0;
edgeList.sort(Comparator.comparingDouble(o -> o.dist));
for (StarEdge starEdge : edgeList) {
if (find(starEdge.start) == find(starEdge.end)) {
continue;
}
union(starEdge.start, starEdge.end);
answer += starEdge.dist;
cnt++;
if (cnt == len - 1) {
break;
}
}
System.out.println(answer);
}
static boolean union(int x, int y) {
x = find(x);
y = find(y);
if (x == y) {
return false;
}
parents[y] = x;
return true;
}
static int find(int x) {
if (x == parents[x]) {
return x;
}
return parents[x] = find(parents[x]);
}
static double calDist(double x1, double x2, double y1, double y2) {
return Math.sqrt(Math.pow(Math.abs(x1 - x2), 2) + Math.pow(Math.abs(y1 - y2), 2));
}
static class StarEdge {
int start;
int end;
double dist;
public StarEdge(int start, int end, double dist) {
this.start = start;
this.end = end;
this.dist = dist;
}
}
static class Star {
int id;
double x;
double y;
public Star(int id, double x, double y) {
this.id = id;
this.x = x;
this.y = y;
}
}
}앞 부분은 초기화 하고 거리구하는 부분이라 건너띄고 이 부분만 확인하면 될 것 같다.
double answer = 0.0;
int cnt = 0;
edgeList.sort(Comparator.comparingDouble(o -> o.dist));
for (StarEdge starEdge : edgeList) {
if (find(starEdge.start) == find(starEdge.end)) {
continue;
}
union(starEdge.start, starEdge.end);
answer += starEdge.dist;
cnt++;
if (cnt == len - 1) {
break;
}
}거리 오름차순으로 간선 목록을 정렬해주고 순회하면서
근본이 같다면 스킵, 그렇지 않다면 근본 동기화를 해준다.
근본을 동기화할 수 있었다는 것은 해당 노드들 간 새로운 간선을 연결했다는 것을 의미하니 해당 간선의 거리를 최종으로 구할 비용의 일부가 될 수 있다.
