Union Find (예제 : boj 1717 집합의 표현)

강신현·2023년 1월 25일

Union Find

상호 배타적 집합(disjoint set)을 표현하는데에 쓰는 자료구조이다.
상호 배타적 집합은, 서로 공통원소가 없는 집합을 의미한다.

필요한 이유

어떤 파티에 n명의 사람이 왔다고 하자. 레크레이션 강사가 생일이 같은 사람들끼리 뭉치라고 했을 때, 처음에는 모두 혼자 돌아다니다, 생일이 같은 사람을 찾게 되면 그 사람들 끼리는 팀을 이루어 함께 움직이게 된다. 다른 팀을 만났을 때, 생일이 같다는것을 알게 되면 두 팀은 뭉쳐서 한 팀을 구성하는 식으로 움직인다.

파티에 온 사람들의 전체 집합으로 놓고 보면, 팀은 이 집합을 여러개의 부분집합으로 쪼갠것 이다. 각 팀은 생일이 같은 사람들로 구성되었기 때문에, 두 개 이상의 팀에 속한 사람은 없다는 점에 유의하자. 이렇게 공통 원소가 없는, 다시말해 상호 배타적인 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료 구조가 바로 유니온-파인드 구조이다.

이러한 것들을 컴퓨터 언어에서 다룰 수 있게 해주는 유니온-파인드 구조가 할 수 있어야 하는 연산은 다음과 같다.

초기화 : n개의 원소가 각각의 집합에 포함되어 있도록 초기화

합치기(union) 연산 : 두 원소 a,b가 주어질 때, 이들이 속한 두 집합을 하나로 합침

찾기(find) 연산 : 어떤 원소 a가 주어질 때 이 원소가 속한 집합을 반환

초기화 연산은 처음 구조를 만들때 외에는 그렇게 자주 쓰지 않으니, 상대적으로 자주 쓰는 두 연산의 이름을 따서 union-find 자료구조라고 한다.

구현1 (배열)

union-find 자료구조를 구현하는 가장 간단한 방법은 1차원 배열 하나를 이용해서 아래와 같이 만드는 것이다.

belongsTo[i] = i번 원소가 속하는 집합의 번호

처음에는 belongsTo[i] = i로 두면, 찾기 연산을 상수 시간안에 할 수 있다.

하지만 이 방법의 문제는 합치기 연산이다. 합치기 연산을 위해서는 belongsTo[]의 모든 원소를 순회하면서 한쪽 집합에 속한 원소들을 다른쪽 원소의 집합으로 옮겨야 하는데, 모든 원소를 순회하는데에는 O(N)의 시간이 걸린다.

찾기 연산이 O(1)이라는 사실은 매우 좋으나, 합치기 연산의 비용이 크기 때문에 다른 방법을 고안해볼 필요가 있다.

구현2 (트리)

배열표현의 "합치기 연산이 느리다"라는 단점을 극복하는 좋은 방법 중 하나는, 트리를 이용해서 이를 구현하는 것이다.

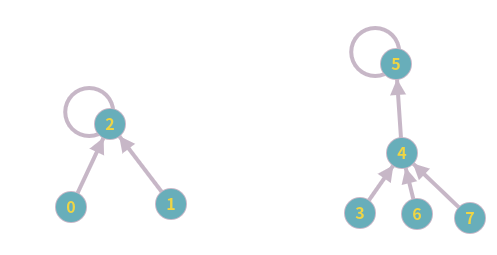
두 원소가 같은 트리에 속해있는지 확인하는 방법인 찾기(find) 연산
👉 원소가 속해있는 트리의 루트가 같은지를 비교하는 것

int parent[1000001];

int find(int node){ // 같은 집합인지 확인 (같은 뿌리인지 확인)
    if(parent[node] == node) return node; // 뿌리 노드일 경우 본인 리턴
    else return parent[node] = find(parent[node]); // 경로 압축 최적화
}

void uni(int a, int b){ // 합집합 (a 집합을 b 집합의 자식노드로 합침)
    int rootA = find(a);
    int rootB = find(b);

    parent[rootA] = rootB;
}

void init(){ // 부모 배열 초기화
    for(int i=0;i<=n;i++){
        parent[i] = i;
    }
}

트리와 루트는 항상 1:1 대응되므로(루트가 2개 이상 있는 트리는 존재하지 않으니까) 루트가 같다면 두 원소가 같은 트리에 있음을 자명하게 알 수 있다.
위의 연산을 구현하기 위해서 자식 노드들이 부모 노드의 정보를 알고 있어야 한다.
- 하지만, 부모 노드는 자식 노드에게 갈 일이 없기 때문에 자식 노드에 대한 정보를 저장할 필요가 없다.
- 또, 루트는 그 부모가 없으므로, 자기 자신을 부모로 지정한다.

시간복잡도

find()의 시간 복잡도는 대상이 되는 트리의 높이에 비례하는 시간이 걸린다.
집합(트리)을 합치는 uni()함수의 시간복잡도 또한 find가 지배하기 때문에, 이 역시 트리의 높이에 비례한다.

- 최적화 (경로 압축 최적화)

find(u)를 통해서, 찾아낸 u가 속한 트리의 루트를 parent[u]에 반영한다면, 다음에 find(u)가 호출되었을 때, 경로를 찾아갈 필요 없이 빠르게 루트를 찾을 수 있다.

예제 : boj 1717 집합의 표현

https://www.acmicpc.net/problem/1717

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

int n, m;
int u, a, b;
int parent[1000001];

int find(int node){ // 같은 집합인지 확인 (같은 뿌리인지 확인)
    if(parent[node] == node) return node; // 뿌리 노드일 경우 본인 리턴
    else return parent[node] = find(parent[node]); // 경로 압축 최적화
}

void uni(int a, int b){ // 합집합 (a 집합을 b 집합의 자식노드로 합침)
    int rootA = find(a);
    int rootB = find(b);

    parent[rootA] = rootB;
}

void init(){ // 부모 배열 초기화
    for(int i=0;i<=n;i++){
        parent[i] = i;
    }
}

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    cin >> n >> m;

    init();

    for(int i=0;i<m;i++){
        cin >> u >> a >> b;

        if(u == 0){
            uni(a,b);
        }
        if(u == 1){ 
            if(find(a) == find(b)) cout << "YES" << "\n";
            else cout << "NO" << "\n";
        }
    }

    return 0;
}