차원축소(PCA, LDA)

머신러닝에 있어서 차원축소는 왜 필요할까?

---

출처: minye-lee19.gitbook.io

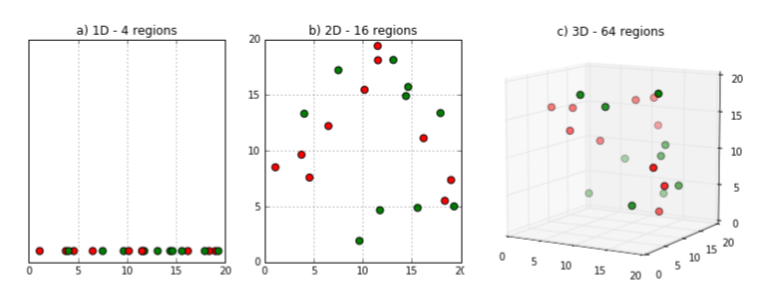
위의 그림을 참고해보자 a->b->c 순으로 차원이 커짐을 알 수 있다. 차원이 커지면 데이터 포인트들 간의 거리가 크게 늘어나고 데이터가 희소화(Sparse)된다. (데이터들이 차원이 늘어남에 따라 세분화 되서 학습에 사용될 데이터가 줄어든다고 이해하면된다)

이에 따라 차원이 늘어나 수백, 수천개 이상의 피처로 구성될 때 포인트들 간 거리에 기반한 ML알고리즘은 무력화된다.
또한 피처가 많을 경우 개별 피처 간에 상관관계가 높아질 확률이 높아서 선형회귀와 같은 모델에서는 다중 공선성 문제로 모델의 예측 성능이 저하될 가능성이 높다

차원축소의 장점은 뭘까?

수많은 피처들을 작은 수의 피처들로 축소한다고 생각해보자
1. 학습데이터 크기를 줄여서 학습시간을 절약할 수 있다
2. 불필요한 피처들을 줄여서 모델 성능 향상에 기여할 수 있다
3. 다차원의 데이터를 3차원 이하의 차원 축소를 통해서 시각적으로 보다 쉽게 패턴을 인지할 수 있다
4. 다차원의 데이터를 차원축소시켜 더 데이터를 잘 설명할 수 있는 잠재적(Latent)인 요소를 추출할 수 있다.

=>그럼 어떻게 해야 원본 데이터의 정보를 최대한 유지한 채로 차원축소를 할 수 있을까?

Feature selection과 Feature Extraction

일반적으로 차원축소는 피처선택과 피처 추출로 나눌 수 있다.

피처선택(Feature selection): 특정 피처에서 종속성이 강한 불필요한 피처는 아에 제거하고 데이터의 특징을 잘 나타내는 주요 피처만 선택하는것이다.

피처추출(Feature Extracion): 피처추출은 기존 피처를 저차원의 중요한 피처로 압축해서 추출하는 것이다. 이렇게 새롭게 추출된 주요 특성은 기존의 피처를 반영해 압축된 것이지만 새로운 피처로 추출하는 것이다.이는 단순 압축이 아닌 더 잘 설명할 수 있는 잠재되어(latent)있는 특성을 또다른 공간으로 매핑해 추출하는 것이다.

ex) 학생 평가 시 - 모의고사성적, 봉사활동, 내신성적, 수능성적, 대외활동 등을 요약해서 더 낮은 피처로 표현하고자면 학업 성취도,문제해결력 등으로 축소 할 수 있다.

PCA(Principal Component Analysis)

차원축소하는 기법으로 고차원의 원본데이터를 저차원의 부분공간으로 투영하여 데이터를 축소하는 기법 ex) 20차원으로 2차원으로 만듬
PCA는 원본 데이터가 가지는 데이터의 변동성을 가장 중요한 정보로 간주하여 이 변동성에 기반한 원본 데이터 투영으로 차원축소를 한다

이때 가장 핵심은 어떻게 원본 데이터를 최소한으로 훼손시킬지 이다

PCA의 적용방식

PCA는 원본 데이터 간의 상관관계가 있다고 가정하고 압축을 진행한다. 원본 데이터 변동성(Variance)이 가장 큰 방향으로 순차적으로 축을 생성하고 이렇게 생성된 축으로 데이터를 투영하는 방식이다. 이처럼 첫번째 축이 만들어지면 두번째 축은 첫번째 축을 제외하고 그다음으로 변동성이 큰 축을 설정하는데 이는 첫번째 축에 직각이 되는 벡터(직교 벡터)축이다. 세번째 축은 다시 두번째 축과 직각이 되는 벡터를 설정하는 방식으로 축을 생성한다. 이렇게 생성된 벡터 축은 원본 데이터를 투영하면 벡터 축의 개수만큼 차원으로 원본 데이터가 차원축소된다.

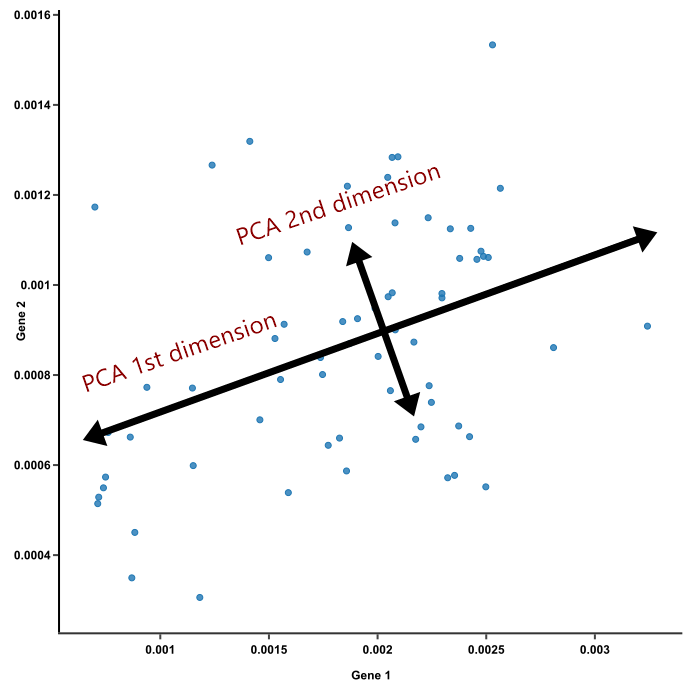
출처 : https://blog.bioturing.com/2018/06/14/principal-component-analysis-explained-simply/
PCA는 이처럼 원본데이터의 피처 개수에 비해 매우 작은 주성분으로 원본 데이터의 총 변동성을 대부분 설명할 수 있는 분석법이다.

PCA변환

PCA를 선형대수관점에서 해석해보면, 입력데이터의 공분산 행렬(Covariance Matrix)을 고유값 분해하고, 이렇게 구한 고유벡터(eigen vector)에 입력데이터를 선형변환하는것이다.

원본데이터의 공분산 행렬추출 -> 공분산 행렬을 고유벡터와 고유값 분해 -> 원본데이터를 고유벡터로 선형변환 -> PCA 변환값 도출

고유벡터는 PCA의 주성분 벡터로써 입력 데이터의 분산이 큰 방향을 나타낸다. 고유값은 바로 이 고유벡터의 크기를 나타내며, 동시에 입력 데이터의 분산을 나타낸다.

중간 행렬 개념들

• 공분산 행렬
  보통 분산은 한개의 특정한 변수의 데이터 변동을 의미하나, 공분산은 두 변수간의 변동을 의미한다. 즉, 사람 키 변수를 x, 몸무게 변수를 y라고 하면 공분산 cov(x,y)>0은 x(키)가 증가할때 y(몸무게)도 증가한다는 의미이다. 공분산 행렬은 여러 변수와 관련된 공분산을 포함하는 정방형 행렬이며 대칭행렬이다. 정방행렬은 열과 행이 같은 행렬은 지칭하는데, 정방행렬 중에서 대각 원소를 중심으로 원소 값이 대칭되는 행렬, 즉 A.T =A인 대칭행렬이라부른다.

• 선형 변환과 고유벡터/고유값
  일반적으로 선형변환은 특정 벡터에 행렬 A를 곱해 새로운 벡터로 변환하는 것을 의미한다. 이는 특정 벡터를 하나의 공간에서 다른 공간으로 투영하는 개념으로도볼 수 있으며, 이 경우 이행렬을 바로 공간으로 가정하는 것이다. 고유벡터는 행렬 A를 곱하더라도 방향이 변하지 않고 그 크기만 변하는 벡터를 지칭한다. 즉 Ax=ax(A는 행렬, x는 고유벡터,a는 스칼라 값)이다.(원래는 람다인디...ㅋ)

이 고유벡터는 여러개가 존재하며, 정방행렬은 최대 그 차원 수 만큼 고유 벡터를 가질 수 있다. 예를 들어 22 행렬은 두개의 고유벡터를, 33행렬은 3개의 고유벡터를 가질 수 있다. 이렇게 고유벡터는 행렬이 작용하는 힘의 방향과 관계가 있어서 행렬을 분해하는데 사용된다.

PCA변환과 수행절차 정리

PCA변환
입력 데이터의 공분산 행렬이 고유벡터와 고유값으로 분해될 수 있으며, 이렇게 분해된 고유벡터를 이용해 입력 데이터를 선형 변환하는 방식

PCA 변환 수행절차
1. 입력 데이터 세트의 공분산 행렬을 생성한다.
2. 공분산 행렬의 고유벡터와 고유값을 계산한다.
3. 고유값이 가장 큰 순으로 K개(PCA 변환 차수만큼)만큼 고유벡터를 추출한다.
4. 고유값이 가장 큰 순으로 추출된 고유벡터를 이용해 새롭게 입력데이터를 변환한다.

사이킷런 PCA 사용법

scikit-learn은 pca를 지원한다
중요: PCA를 사용하기 전에 입력 데이터의 개별 피처들을 스케일링 해야한다. PCA는 여러 피처들의 값을 연산해야 하므로 피처들의 스케일에 영향에 받는다. 따라서 여러 속성을 PCA로 압축하기 전에 각 피처들의 값을 동일한 스케일로 변환하는 것이 필요하다.

n_components는 PCA 축의 개수, 즉 변환 차원을 의미한다.
PCA변환이 완료된 사이킷런 PCA 객체는 전체 변동성에서 개별 PCA 컴포넌트별로 차지하는 변동성 비율을 explained_variance_ratio 속성으로 제공한다.

이때 fit과 transform을 따로 할 수도 있고 fit_transform으로 한번에 할 수도 있다.

LDA(Linear Discriminant Analysis)

LDA는 선형 판별 분석법으로 불리며 PCA와 유사하다
LDA는 PCA와 유사하게 데이터 세트를 저차원 공간에 투영해 차원을 축소하는 기법이지만, 중요한 차이는 LDA는 지도학습의 분류에서 사용하기 쉽도록 개별 클래스를 분별할 수 있는 기준을 최대한 유지하면서 차원을 축소한다. PCA는 입력 데이터의 변동성의 가장 큰 축을 찾았지만, LDA는 입력 데이터의 결정 값 클래스를 최대한으로 분리할 수 있는 축을 찾는다.
LDA는 같은 클래스의 데이터는 최대한 근접해서, 다른 클래스의 데이터는 최대한 떨어뜨리는 축 매핑을 한다.

LDA 차원 축소 방식

LDA는 특정 공간 상에서 클래스 분리를 최대화하는 축을 찾기 위해 클래스 간 분산(between-class scatter)과 클래스 내부 분산(within-class scatter)의 비율을 최대화하는 방식으로 차원을 축소한다. 즉, 클래스 간 분산은 최대한 크게 가져가고, 클래스 내부의 분산은 최대한 작게 가져가는 방식이다.

LDA절차

일반적으로 LDA를 구하는 스탭은 PCA와 유사하나 가장 큰 차이점은 공분산 행렬이 아니라 앞에서 설명한 클래스 간 분산과 클래스 내부 분산행렬을 생성한 뒤, 이 행렬에 기반해 고유벡터를 구하고 입력 데이터를 투영한다는 점이다.
1. 클래스 내부와 클래스 간 분산 행렬을 구한다. 이 두개의 행렬은 입력데이터의 결정값 클래스 별로 개별 피처의 평균벡터를 기반으로 구한다.
2. 클래스 내부 분산 행렬을 S_w, 클래스 간 분산행렬을 S_b라고 하면 다음 식으로 두 해열ㄹ을 고유벡터로 분해할 수 있다.
3. 고유값이 가장 큰 순으로 K개(LDA변환 차수만큼)추출한다
4. 고유값이 가장 큰 순으로 추출된 고유벡터를 이용해 새롭게 입력데이터를 변환한다.

PCA와 차이점

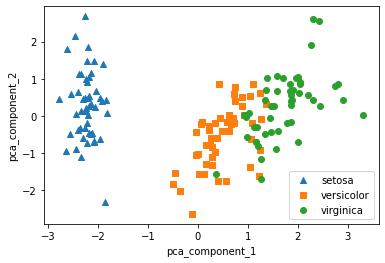
PCA는 비지도학습에 쓰이므로 label이 필요하지 않고 데이터의 구조나 패턴을 기반으로 차원을 축소한다. 따라서 전반적인 구조나 패턴을 파악하려는 경우, 레이블 정보가 없는 경우 PCA가 더 적합하다

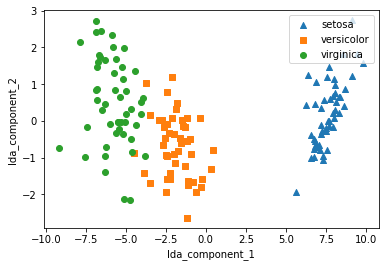
LDA는 지도학습에 쓰이므로 label값이 필요하고 레이블 간의 구별력을 최대화하는 방향으로 차원을 축소한다. 따라서 차원축소의 목적이 분류이면 LDA가 더 효과적인 경향이 있다. 이는 clustering과 유사하다.

수학적 접근

PCA는 변동성(분산)이 가장 큰 축을 찾는다

LDA는 클래스를 최대한으로 분리할 수 있는 축을 찾습니다. 여기에 내부 클래스간의 분산은 최소화한다.

나 데이터의 전반적인 구조나 패턴을 파악하려는 경우나 레이블 정보가 없는 경우 PCA가 더 적합할 수 있습니다