PS#7 그래프 이론

그래프 종류

• 양방향 그래프
• 단방향 그래프

표현방법

1. 인접 행렬

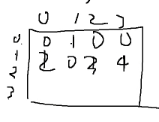
Node가 n개 있을 때, n * n 행렬로 구현.

갈 수 있는 경우(간선이 존재하는 경우) 1.
갈 수 없는 경우(간선이 존재하지 않는 경우)0.

가중치를 주고싶은 경우, 1이 아닌 가중치로 써줘도 좋음.

---

2. 인접 그래프

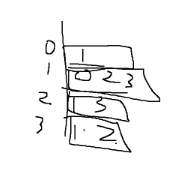
벡터를 사용함.

그래프 생성

---

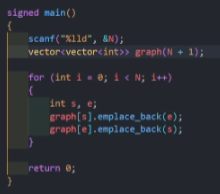
DFS, BFS랑 섞어씀.

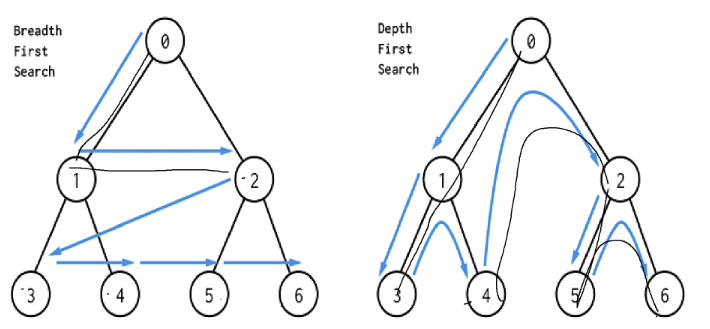
DFS

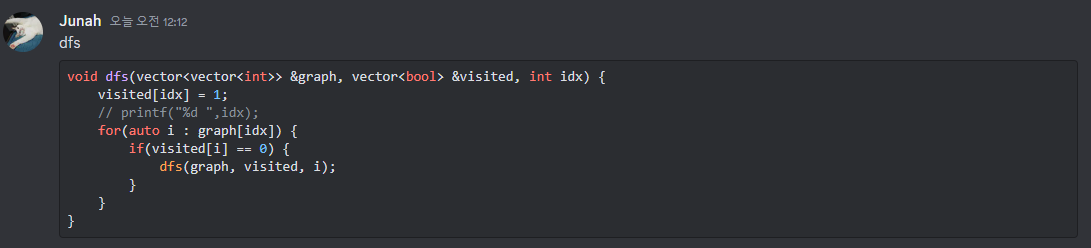
void dfs(vector<vector<int>> &graph, vector<bool> &visited, int idx) {
    visited[idx] = 1;
    // printf("%d ",idx);
    for(auto i : graph[idx]) {
        if(visited[i] == 0) {
            dfs(graph, visited, i);
        }
    }
}

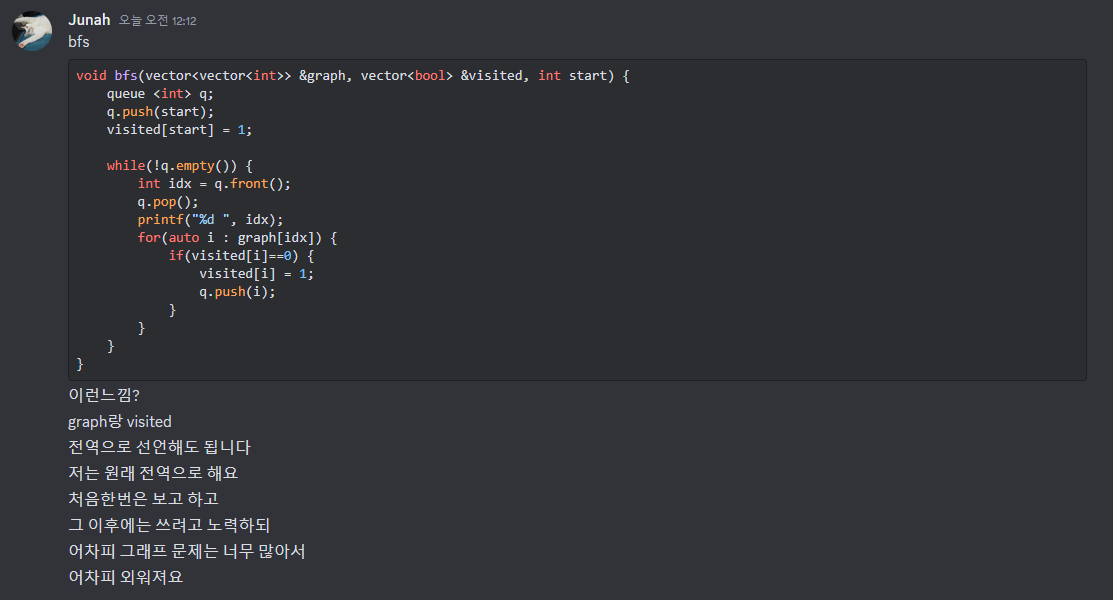
void bfs(vector<vector<int>> &graph, vector<bool> &visited, int start) {
    queue <int> q;
    q.push(start);
    visited[start] = 1;

    while(!q.empty()) {
        int idx = q.front();
        q.pop();
        printf("%d ", idx);
        for(auto i : graph[idx]) {
            if(visited[i]==0) {
                visited[i] = 1;
                q.push(i);
            }
        }
    }
}

전역으로 선언하는 그래프와 노드 방문 벡터에 필요한 N은 아래와 같이 핸들링

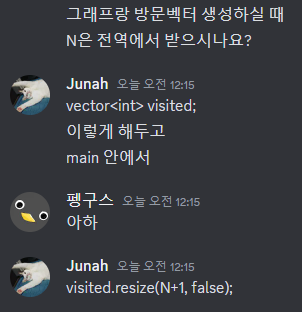
before

#include <iostream>
#include <vector>
using namespace std;

int main()
{
  int N, M, R;
  cin >> N >> M >> R;
  
  vector<bool> visited(N + 1, false);
  vector<int> need_visit(N + 1);
  vector<vector<int>> v(N + 1);

  for (int i = 0; i < M; i++)
  {
    int s, e;
    cin >> s >> e;
    v[s].emplace_back(e);
    v[e].emplace_back(s);
  }

  return 0;
}

after

#include <iostream>
#include <vector>
using namespace std;

vector<bool> visited;
vector<vector<int>> v;

int main()
{
  int N, M, R;
  cin >> N >> M >> R;
  visited.resize(N + 1, false);
  v.resize(N + 1);
  
  for (int i = 0; i < M; i++)
  {
    int s, e;
    cin >> s >> e;
    v[s].emplace_back(e);
    v[e].emplace_back(s);
  }

  return 0;
}