유클리드 호제법(Euclidean algorithm)

최소공배수를 구할 때, 유용하게 사용되는 알고리즘이다.

최소공배수를 구하는 알고리즘과 원리는 아래의 gif가 직관적으로 설명한다.

---

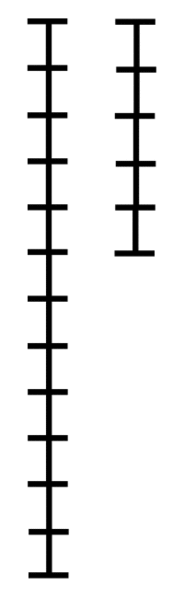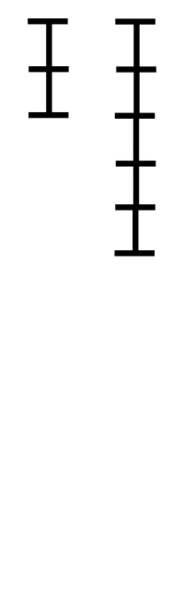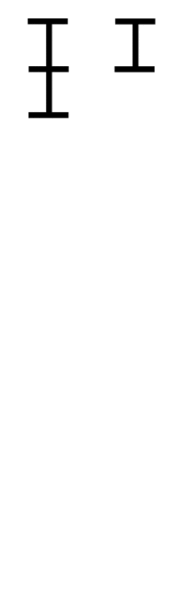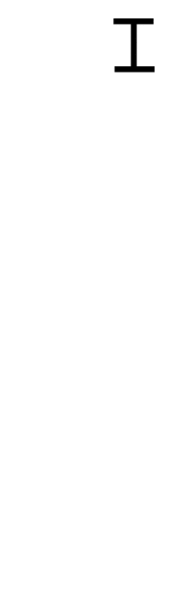
재귀함수를 통한 최대공약수 구현

- 최대공약수(Greatest Common Divisor)

const getGCD = (x, y) => {
  if (y === 0) return x;
  return getGCD(y, x % y);
}

//shortcut
const getGCD = (x, y) => (y ? getGCD(y, x % y) : x);

- 두 개 이상의 수에 대한 최대공약수

function solution(arr) {
  let GCD = arr[0];
  for (let i = 1; i <= arr.length - 1; i++) {
    BGCD = getGCD(BGCD, arr[i]);
  }

---

재귀함수를 통한 최소공배수 구현

- 최소공배수(Least Common Multiple)

const getGCD = (x, y) => (y ? getGCD(y, x % y) : x);
const getLCM = (x, y) => (x * y) / getGCD(x, y);

- 두 개 이상의 수에 대한 최소공배수

//arr:number[];
function solution(arr) {
  let LCM = arr[0];
  for (let i = 1; i <= arr.length - 1; i++) {
    LCM = getLCM(LCM, arr[i]);
  }

  return LCM;
}

const getGCD = (x, y) => (y ? getGCD(y, x % y) : x);
const getLCM = (x, y) => (x * y) / getGCD(x, y);

---

프로그래머스 카드 나누기 문제

> ref

위의 문제는 유클리드 호제법을 이용해 풀이할 수 있다.

function solution(arrayA, arrayB) {
    var answer = 0;
    
    let AGCD = arrayA[0];
    for (let i = 1; i <= arrayA.length - 1; i++) {
        AGCD = getGCD(AGCD, arrayA[i])
    }  
    
    let BGCD = arrayB[0];
    for (let i = 1; i <= arrayB.length - 1; i++) {
        BGCD = getGCD(BGCD, arrayB[i])
    }
    
    for (let i of arrayA) {
        let dividable = isDividable(i, BGCD);  
        if (dividable) {
            BGCD = 0;
            break;
        };
    }
    
    for (let i of arrayB) {
        let dividable = isDividable(i, AGCD);  
        if (dividable) {
            AGCD = 0;
            break;
        };
    }
    
    answer = Math.max(AGCD, BGCD)
    
    return answer;
}

const getGCD = (x, y) => y ? getGCD(y, x % y) : x;

const isDividable = (number, dividor) => {
    const remain = number % dividor;
    if (remain === 0) return true;
    return false;
}

/* 기능명세
- [x] A와 B의 GCD를 구한다.
- [x] 각 배열의 가장 큰 값과 반대의 GCD를 비교한다. GCD가 더 크다면, 해당 배열은 나눌 수 없다.
- [x] 상대 패를 나눌 수 있는지 확인한다.
- [x] 하나라도 나눠질 경우, 0을 return한다.
- [x] 전부 나눠지지 않는다면 해당 값을 return한다.
*/