다익스트라 알고리즘

다익스트라(Dijkstra) 알고리즘이란?
음의 가중치가 없는 그래프에서 한 정점(vertex)에서 다른 모든 정점까지 가는 최단경로를
구하는 것을 말한다.

음의 가중치가 없다는 게 무슨 뜻일까?

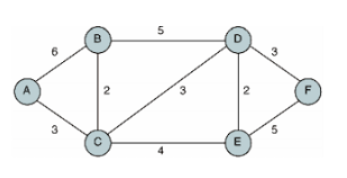
위 그림을 기준으로 볼 때 A<->B로 볼 때 이동거리가 6이다.
이동거리를 가중치라고 표현하기도 하고 비용이라고도 하기도 한다.
다익스트라 알고리즘을 적용하려면 이동거리가 음수가 나오면 안된다는 뜻이다.

음의 가중치가 나오면 다익스트라를 쓸 수 없는 이유

가중치가 음이 나온 경우 다익스트라 알고리즘으로 최소경로를 구할 수 없는데
그 이유는 다익스트라 알고리즘은 현재 노드를 기준으로 최소 비용인 노드로 이동하는 방식인데
음수면 그 경로를 반복해서 왔다갔다 하기도 하고
더 낮은 비용의 값이 나오면 갱신을 하는데 음의 가중치가 있으면 무한 갱신되기 때문이다.

다익스트라를 구하는 2가지 방법

1. 완전 탐색
2. 우선순위 큐(최소 힙) 사용
   A->B->C->D일 때
   A->B->C까지 구했다면 기존에 이동했던 거리를 저장하고 꺼내는 과정이 필요한데
   그 꺼내는 것을 그냥 전부 저장해놓고 뽑아서 쓰느냐
   우선순위 큐로 최소값만 저장해서 쓰느냐 차이다.

다익스트라 순서

1. 최단거리를 저장할 배열 생성 및 초기값 설정
   출밤점으로부터의 최단거리를 저장한 배열 distance[vertex]를 만들고
   출발 노드에는 0을, 출발점을 제외한 다른 노드들에는 무한으로 간주될 수 있는 값 Infinite를
   할당한다. 일단적으로 데이터 타입의 최대값으로 할다한다.
2. 현재 노드 current에 출발 노드의 번호를 저장한다.
3. 최단 경로 계산 후 할당
   현재 노드를 A, 이동할 노드를 B라고 할 때
   임의의 두 노드 A->B로 갈때 distances[A]와 A에서 B까지의 최단경로 shortestPath[A][B]라고 할 때 distance[A]+shortestPath[A][B] < distance[B]이면
   distance[B] = distance[A]+shortestPath[A][B]로 할당한다.
   초기값이 무한으로 간주는 되는 값 Infinite이므로 갱신된다.
   모든 인접한 노드에 대해서 위 과정을 반복한다.
4. 방문 완료 표시
   current의 모든 인접 노드의 최단경로를 구했다면 "방문 완료"로 바꾼다.
5. "미방문" 상태인 모든 노드들 중, 출발점으로 부터 거리가 제일 짧은 노드 하나를 골라
   current에 저장한다. 도착 노드가 "방문 완료"상태가 되거나, 더 이상 미방문 상태의 노드를
   선택할 수 없을 때까지, 반복한다.
6. 도착 노드에 저장된 값이 바로
   이 작업을 마친 뒤, 도착 노드에 저장된 값이 바로 A로부터의 최단 거리이다. 만약 이 값이 INF라면, 중간에 길이 끊긴 것임을 의미한다.

예제 문제와 코드

다익스트라를 잘 이해하기 위해 예제 문제와 함께 알아보자.
백준 4485번
https://www.acmicpc.net/problem/4485

import sys
import heapq
input = sys.stdin.readline

n = int(input())
# 남,동,서,북
direction_x = [0,1,-1,0]
direction_y = [1,0,0,-1]
count = 0

while n != 0:
    # 입력받기
    count+=1
    board = [list(map(int,input().split())) for _ in range(n)]
    distance = [[float('inf')]*n for _ in range(n)]

    # 최단 경로를 저장하는 최소 힙
    heap = []
    
    # 최소힙인 heap에 (board[0][0],0,0)을 넣는다.
    heapq.heappush(heap, (board[0][0], 0, 0))

    while heap:
        # heap에서 가장 작은 값을 pop한다.
        cost,x,y = heapq.heappop(heap)

        # 최소 가중치를 먼저 가기 때문에 [n-1][n-1]에 도착하면 break한다.
        if x==n-1 and y==n-1:
            print(f"Problem {count}: {cost}")
            n = int(input())
            break
        # 남,동,서,북으로 이동한다.
        for i in range(4):
            next_x = x+direction_x[i]
            next_y = y+direction_y[i]
            # 이동한 좌표가 범위 내에 있으면
            if 0<=next_x<n and 0<=next_y<n:
                # 이동한 좌표의 가중치가 현재 가중치+이동한 좌표의 가중치보다 크면
                if distance[next_y][next_x] > cost+board[x][y]:
                    # 이동한 좌표의 가중치를 현재 가중치+이동한 좌표의 가중치로 갱신한다.
                    distance[next_y][next_x] =  cost+board[x][y]
                    # heap에 (현재 가중치+이동한 좌표의 가중치,이동한 y좌표,이동한 x좌표)를 넣는다.
                    heapq.heappush(heap, (cost+board[next_y][next_x],next_x,next_y))

벨만 포드

음의 가중치가 있어도 노드 간의 최단거리를 구할 수 있는 알고리즘.
시간복잡도는 정점의 갯수를 V, 간선의 갯수를 E라고 할 때 $O(V\times E)$이다.

• 다익스트라에 비해 "음의 가중치"가 있어도 계산이 가능하다.
• 플로이드 와샬에 비해 시간복잡도가 낮은 편이다.

플로이드 와샬

음의 가중치가 있어도 노드 간의 최단거리를 구할 수 있는 알고리즘.
시간복잡도는 정점의 갯수를 V라고할 때 $O(V^3)$
파이썬으로 구현할 경우 삼중 for문으로 구현이 단순하다.

• 다익스트라에 비해 "음의 가중치"가 있어도 계산이 가능하다.
• 벨만 포드에 비해 구현이 단순하지만 시간복잡도가 높다.

요약

정점의 갯수를 V(Vertex), 간선의 갯수를 E(Edge)라고 할 때

	다익스트라	벨만 포드	플로이드 와샬
음수 가중치가 있을 때	계산 불가	계산 가능	계산 가능
시간 복잡도	$O(V^2)$	$O(V\times E)$	$O(V^3)$
장점	시간 복잡도 낮음	음수 계산 가능, 낮은 시간복잡도	음수 계산 가능,단순한 구현
단점	음수 계산 불가	복잡한 구현	높은 시간복잡도