[배낭문제] 백준 12865 평범한 배낭

백준 12865 평범한 배낭

배낭 문제란?

배낭에 담을 수 있는 최대 무게가 정해져 있고 각각의 무게와 가치가 주어진 물건들이 주어졌을 때 배낭에 담은 물건들의 가치가 최대가 되도록 하게 물건을 고르는 방법을 찾는 문제이다.

배낭 문제 예시

4가지의 물건 A, B, C, D가 있다고 가정하고 배낭의 최대 무게는 7이라고 가정하자

물건	A	B	C	D
가치	13	8	6	12
무게	6	4	3	5

이때 이 가방에 넣을 수 있는 최대 가치가 몇인지를 구해야 한다.

예를 들어 가방의 최대 무게가 7이므로 가치가 8이고 무게가 4인B와 가치가 6이고 무게가 3인 C를 가방에 넣으면 8 + 6 = 14로 가방에 담을 수 있는 최대 가치는 14이다.

이 문제는 브루트 포스 방식으로 풀 수도 있으나 시간 복잡도가 O(2^n)이 되므로 DP(동적 계획법)으로 해결해야 한다.

동적 계획법

DP는 큰 문제를 작은 문제로 쪼개서 푸는 방법이다.

위의 예시처럼 물건 A, B, C, D가 있고 배낭의 무게 제한은 7인 배낭 문제를 다음과 같이 표시할 수 있다

DP({A, B, C, D}, 7);

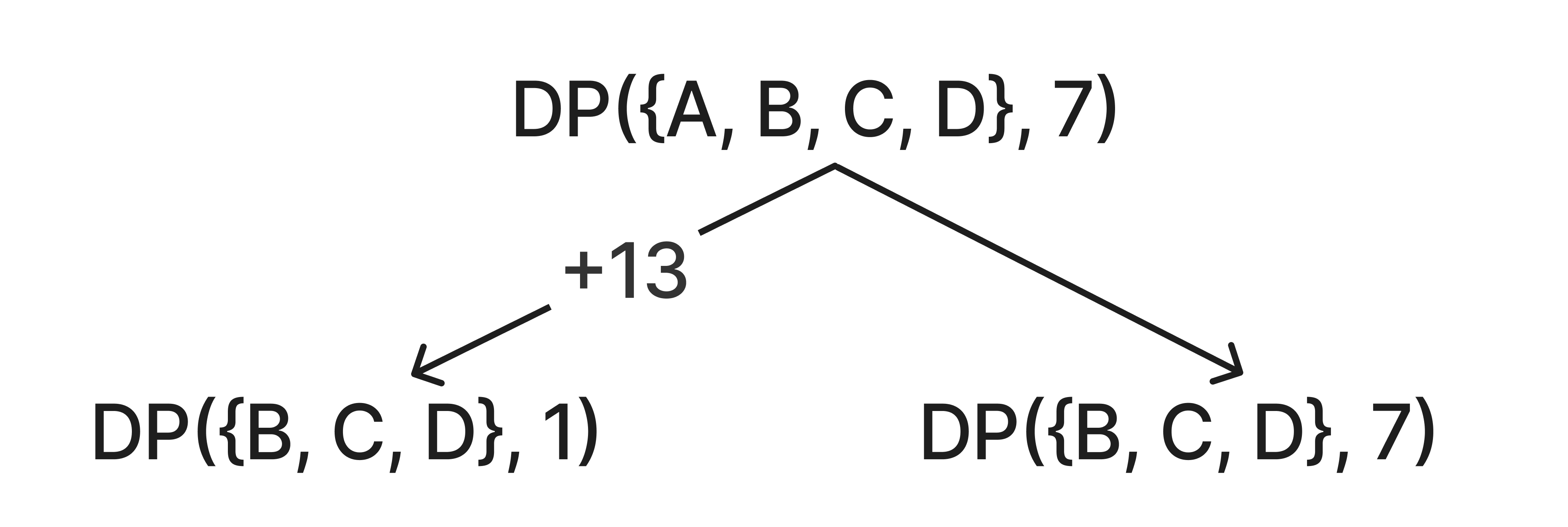
우선 첫번째 물건인 A가 가방에 있는 경우, 없는 경우로 나눌 수 있다.

A가 있는 경우 : DP({B, C, D}, 1) + 13(A가 가방 안에 있어 배낭의 무게제한은 7-6 = 1이 되고, A의 가치 13을 더한다.)
A가 없는 경우 : DP({B, C, D}, 7) + 0

위를 그림으로 표현하면 다음과 같다.

이 경우 물건 B가 가방에 있는 경우와 물건 B가 가방에 없는 경우로 또 나눌 수 있다.

하지만 무게가 음수가 될 수 없으므로 DP({C, D}, -3)의 경우는 지운다.

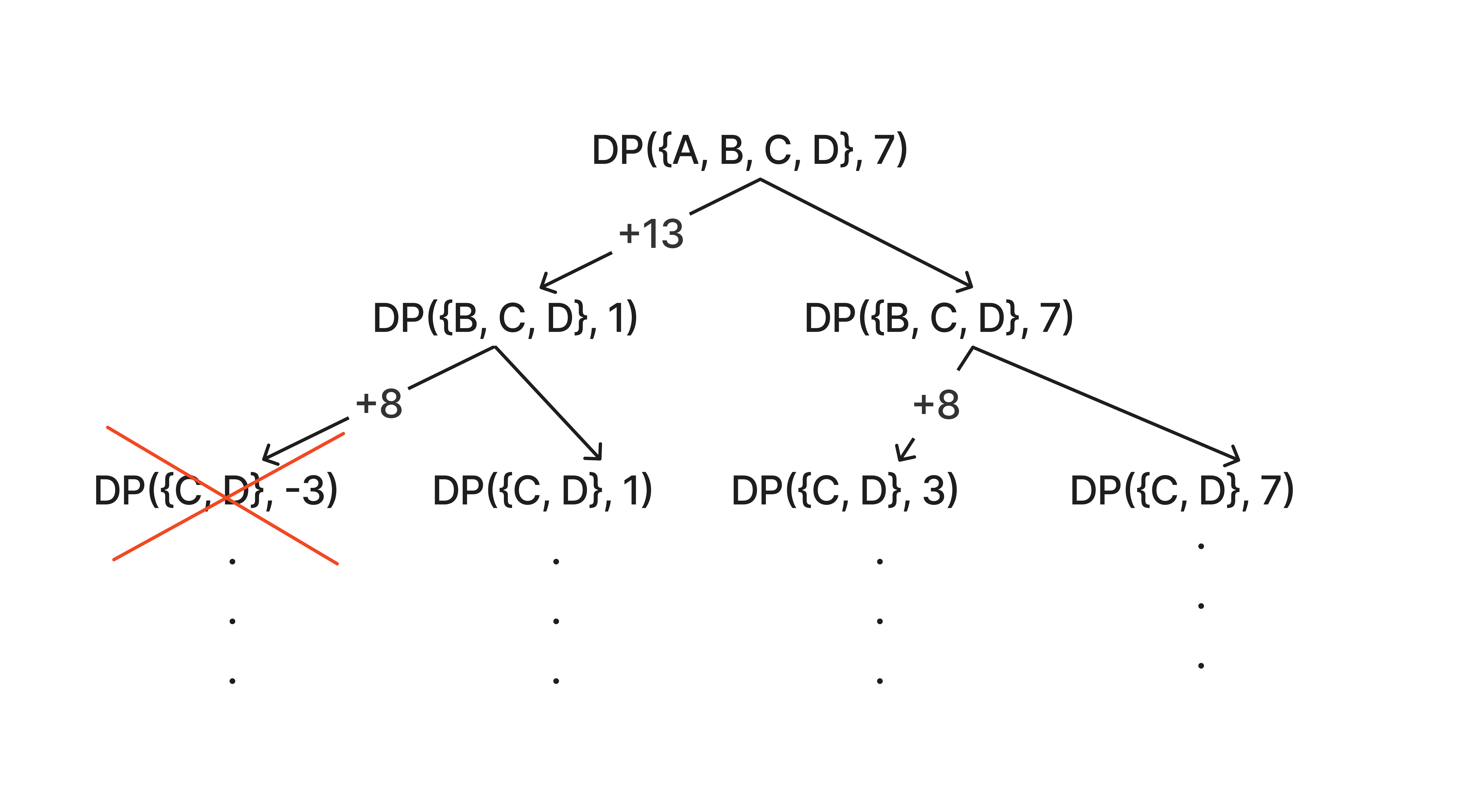
이를 점화식으로 나타낼 수 있다.

DP(N, W) = max{DP(N-1, W-W[n]) + val[n] , DP(N-1,W)}

N : 물건의 개수
W : 현재 상태의 무게 제한

DP(N-1, W-W[n]) + val[n] : n번째 물건을 배낭에 넣은 경우, 해당 물건을 넣었기 때문에 기존 무게에서 n 번째 물건의 무게를 빼주고 n번쨰 물건의 가치를 더해주어야 하므로 val[n]을 더한다.

DP(N-1, W) : n번쨰 물건이 없는 경우, 배낭에 물건을 추가하지 않았으므로 무게는 그대로이다.

이 점화식에는 변수가 N, W 두가지 이므로 2차원 테이블을 만들어서 해결해야 한다.

세로축이 N, 가로축이 W를 나타낸다. 우리는 물건 ABCD가 있고 무게 제한이 7이므로 DP(4, 5) 를 구해야 한다. 즉 아래의 테이블에서 답이라고 표시한 공간을 구해야 한다.

우선 N=0일때, 배낭에 물건을 하나도 넣지 않으면 가치가 0이다. W = 0일때도 배낭에 무게제한이 0이면 배낭에 물건을 하나도 넣을 수 없으므로 가치는 0이다.

N/W	0	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0	0
1(A)	0
2(AB)	0
3(ABC)	0
4(ABCD)	0							(답)

첫번째 경우는 물건 A가 있는 경우와 없는 경우로 나눌 수 있다.

무게 6을 가진 물건 A는 대각선 방향, 즉 물건 A가 있는 경우와 세로 방향으로 가는 경우, 물건 A가 없는 경우가 있다.

대각선으로 가면 가치가 13이 더해지고 세로로 가는 경우 가치가 더해지지 않는다 그리고 각각의 경우에 가방의 한도를 넘지 않는 선에서 둘 중 더 큰 값을 더하면 된다. 따라서 N이 1이고 W가 5까지인 경우 A가 없는 경우가 가장 큰 값이고(0), 6과 7안 경우 A가 있는 경우가 가장 큰 값이 된다(13).

N/W	0	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0	0
1(A)	0	0	0	0	0	0	13	13
2(AB)	0
3(ABC)	0
4(ABCD)	0							(답)

두 번째는 B가 있는 경우와 B가 없는 경우로 나눌 수 있다.
B를 배낭에 넣을 수 없는 경우는 위에서 세로로 내려오고, B를 배낭에 넣을 수 있는 경우는 대각선으로 내려오면서 W가 4만큼 더해지고 가치가 8이 더해진다.

N/W	0	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0	0
1(A)	0	0	0	0	0	0	13	13
2(AB)	0	0	0	0	8	8	13	13
3(ABC)	0
4(ABCD)	0							(답)

세번째 C가 있는 경우와 있는 경우이다.
C를 배낭에 넣을 수 없는 경우는 위에서 세로로 내려오고 있는 경우 대각선으로 내려오면서 무게가 3만큼 더해지고 가치가 6만큼 더해진다.

N/W	0	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0	0
1(A)	0	0	0	0	0	0	13	13
2(AB)	0	0	0	0	8	8	13	13
3(ABC)	0	0	0	6	8	8	8	14
4(ABCD)	0							(답)

N=3, W=3 일 때 C를 배낭에 무게가 3만큼 더해지므로 N=2, W=2에서 가치가 6만큼 더해질 수 있으므로 N=3, W=3인 경우 가치는 6이 된다. N=3, W=4인 경우 N=3, W=3인 경우(6)와 N=2, W=4인 경우(8) 최댓값이 8이므로 N=3, W=4의 가치는 8이 된다.

N=3, W=7인 경우 N=2, W=4인 경우에서 W를 3만큼 더하면서 가치가 6만큼 더해질 수 있으므로 총 가치는 14가 된다. 14와 13을 비교했을 때 14가 더 크므로 N=3, W=7인 경우 14가 채워지게 된다

DP(3, 7) = Max(DP(2,7-3)+6 , DP(2,7)) = 14

네 번쨰 물건D도 마찬가지로 계산해주면 된다.

N/W	0	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0	0
1(A)	0	0	0	0	0	0	13	13
2(AB)	0	0	0	0	8	8	13	13
3(ABC)	0	0	0	6	8	8	8	14
4(ABCD)	0	0	0	6	8	8	8	14

따라서 답은 14가 된다.

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int n = Integer.parseInt(st.nextToken()); //물건 개수
        int k = Integer.parseInt(st.nextToken()); //최대 무게
        int[][] dp = new int[n+1][k+1];//직관성을 높여주기 위해 추가
        int[] w = new int[n+1]; //물건의 무게들
        int[] v = new int[n+1]; //물건의 가치들

        for(int i = 1; i<= n;i++) {
            st = new StringTokenizer(br.readLine());
            w[i] = Integer.parseInt(st.nextToken());
            v[i] = Integer.parseInt(st.nextToken());
        }

        for(int i = 1; i<=n; i++) {
            for(int j = 1; j<=k;j++) {
                if(w[i]<=j) {
                    dp[i][j] = Math.max(dp[i-1][j-w[i]]+v[i],dp[i-1][j]);
                }
                else{
                    dp[i][j] = dp[i-1][j];
                }

            }
        }
        System.out.println(dp[n][k]);
    }
}