(1) Activation Functions

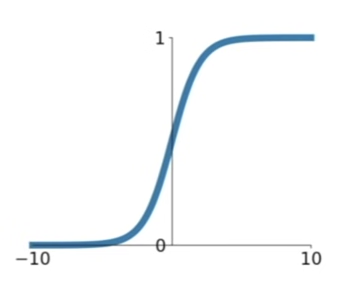
1. Sigmoid

Features

• Squashes numbers to range [0,1] : high values as input - output will be near 1, very negative values as input - output will be near 0

• historically popular since they can be interpretated as a saturating "firing rate" of a neuron

Problems

1. Saturated neurons can "kill off" gradients

   In the back propagation process, we recursively use the chain rule to compute the gradient with respect to every raviable in the computational graph.

   So at each node, remember we have upstream gradients coming backwards -

   However, when using Sigmoid as activation function / non-linearity, the flat parts of the sigmoid (when the X is very negative or very positive) gives gradient of basically something near zero.

   This kills the gradient flow, with having a near-zero gradient getting passed downstream.

   You will not have much coming back in the back propagation.

2. Sigmoid outputs are not zero-centered

   ?????

3. exp() is a bit compute expensive.

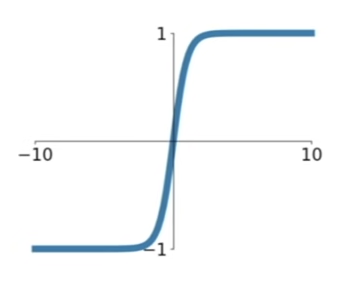
2. tanh(x)

Features

• Squashes numbers to range [-1,1]
• zero-centered ! (fixed the problem 2 from Sigmoid)
• still kills gradients when saturated :( (same problem 1 from Sigmoid)

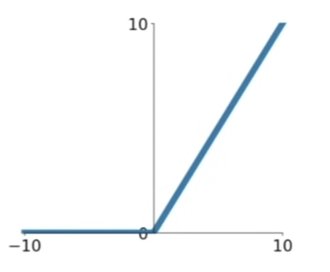
3. ReLU (Rectified Linear Unit)

Features

• Computes f(x) = max(0,x)
  basically, if your input is negative - it will be passed as 0, if it's positive, it will be passed on.
• Does not saturate (in positive region)
• Very computationally efficient
  Sigmoid, tanh has exponential in its function - this is just a max() function.
• Converges much faster than sigmoid / tanh in practice
• Actually more biologically plausible than sigmoid
  (In neuroscientific measurements)
  

Problems

1. Not zero-centered output
2. An annoyance : again in negative half, saturation occurs - killed.

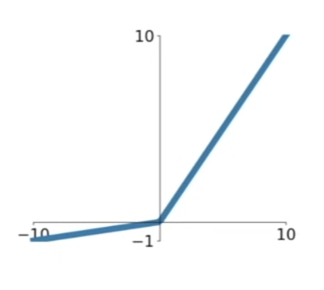
4. Leaky ReLU

Features

1. **Instead of being flat in the negative regime, slight negative slope is given

2. Therefore, does NOT saturate

3. Is still computationally efficient

4. Converges much faster than sigmoid/tanh in practive

5. no dying problem

   Parametric Rectifier (PReLU)

   

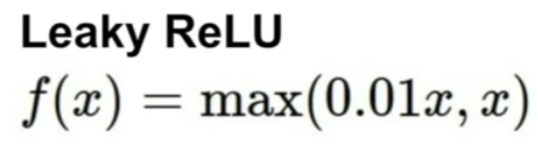
5. Exponential Linear Units

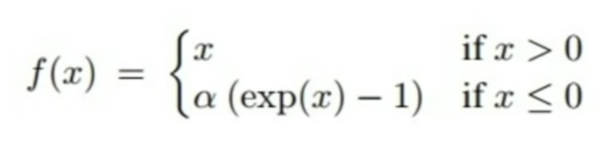
Features

1. All benefits of ReLU
2. Closer to zero mean output
3. Negative saturation regime (compared to Leaky ReLU) adds some robustness to noise

Problems

1. Computation requires exp()

6. Maxout "Neuron"

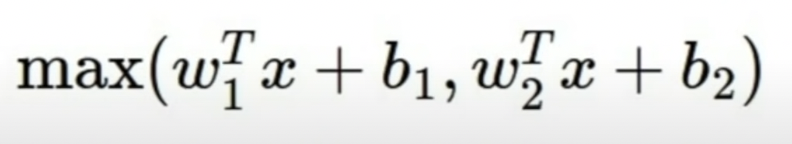
-> takes max of the two linear functions

Features

1. Does not have the basic form of dot product - non-linearity
2. Generalizes ReLU and Leaky ReLU
3. Linear Regime, does not saturate, does not die.

Problems

1. you are doubling the number of parameters per neuron - each neuron now has W1 AND W2

국룰 for Optimization

1. Use ReLU, carefult with learning rate
2. Try Leaky ReLU/ Maxout / ELU - they're still experimental
3. Try tanh - don't expect much, ReLUs will prob be better
4. DO NOT USE SIGMOID

(2) Data Processing

Preprocess Data

With Original Data
1. Zero - mean (zero-centered data)

Does this solve Sigmoid problem?
No, not sufficient. Only helps at first layer.

2. Normalize
   so that all features are in the same range, and thus contribute equally

• in practice, this is not done too much

(3) Weight Initialization

basically you have to START at some value, and then update from there.

1. Do not initialize everything equally - set all the weights as small random numbers that we can sample from a distribution

What happens when W=0 init is used?
-Every neuron is going to do the same thing on the input, and all will give a same output, have the same gradient, same updates, and all the neurons will do the same thing.

Deeper networks