Loss and Regularization

L1 and L2 losses

L1-loss

예측값과 실제값의 사이의 오차 절대값을 계산함.
Least Absolute Deviations (LAD) 라고도 부른다.

L2-loss

예측값과 실제값의 사이의 오차 제곱한 값을 계산함.
Least Square Error (LSE) 라고도 부른다.

Differences between L1 and L2

L2 loss의 경우 제곱의 형태로 오차를 계산하므로 outlier에 영향이 크다. 따라서 노이즈에 예민해야 하는 경우 사용하는 것이 좋다.

L1 loss	L2 loss
Robust	Less robust
Less stable	Stable
Multi-solution	Unique solution

• Robustness: Outlier에 얼마나 강인(둔감)하게 반응하는가
• Stable: 주어진 데이터에 얼마나 General한 예측이 가능한가.

Regularization

머신러닝 기법 중 하나로 모델의 과적합 (Overfitting)을 방지하고자 제안된 방법이다. 모델을 구성하는 계수 (Coefficients)들이 학습데이터에 너무 완벽하게 들어맞게 않게 억제하는 역할이며 L1 regularatizaion 그리고 L2 regularization 두 가지 방식이 있다.

특정 가중치가 너무 큰 값을 같지 않도록 한다.

L1 regularatizaion

L2 regularatizaion

가중치 $W$을 제한하여 너무 커지지 않게한다. W값이 커지면 outlier에 대해서도 loss 값이 더 크게 나올 수 있다.

L1 과 L2 선택하기

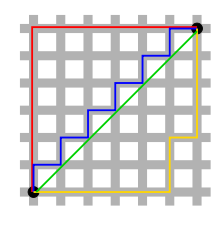
L2-norm의 경우 초록색 선으로 최단거리이면서 동시에 유일한 해이다. 또한Computational cost 측면에서도 유리하다.

반면 L1-norm의 경우 오차절대값의 합이기 때문에 빨간색,파란색,노란색 여러 해를 가진다. 이때 파란색/노란색 대신 빨간색을 선택하여 특정 feature 값을 0으로 만들어 처리하는 것이 가능하다.

L1은 sparse coding에 유리하다.

Refenrecens
1. https://light-tree.tistory.com/125
2. https://junklee.tistory.com/29