BOJ 15483 - 최소 편집

최소 편집 - 🥇 Gold 3

• 문제 링크
  https://www.acmicpc.net/problem/15483

이전에 풀이하였던 BOJ 9251 LCS 와 유사한 형태로 풀이가 가능한 문제다. 문제를 간단히 정리하자면 아래와 같다.

input

• 2개의 문자열이 입력으로 주어짐

output

• 두 문자열이 같아지기 위해 아래와 같은 연산을 함
  - 특정 위치에 문자 하나를 삽입
  - 특정 위치의 문자 하나를 삭제
  - 특정 위치의 문자 하나를 교체
• 위의 연산을 최소로 사용하는 경우의 횟수를 출력

앞에서부터 두 문자열을 비교해가며 문자열을 수정해나가면 될 것이라 생각하였지만, 최소로 연산을 사용해야하기 때문에 같은 문자가 존재할 경우도 고려해야한다. 이를 위해 2차원 배열 DP를 활용하여 풀이한다.

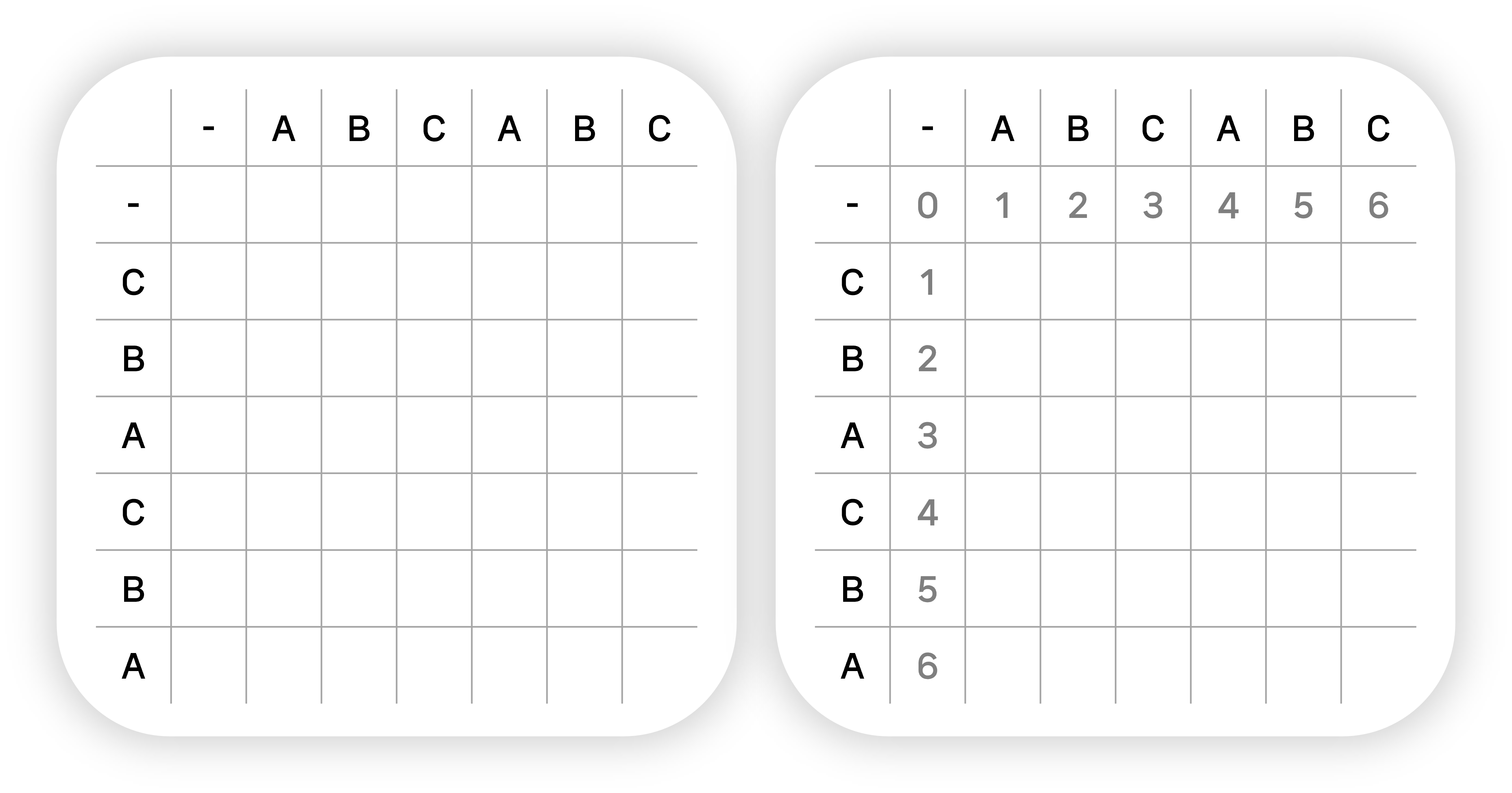
ABCABC와 CBACBA를 예로 들어보자. 각 문자열이 NULL일 경우에는, 각 경우까지 삽입해주는 것이 최소 연산이므로, 이에 대한 값부터 저장한다.

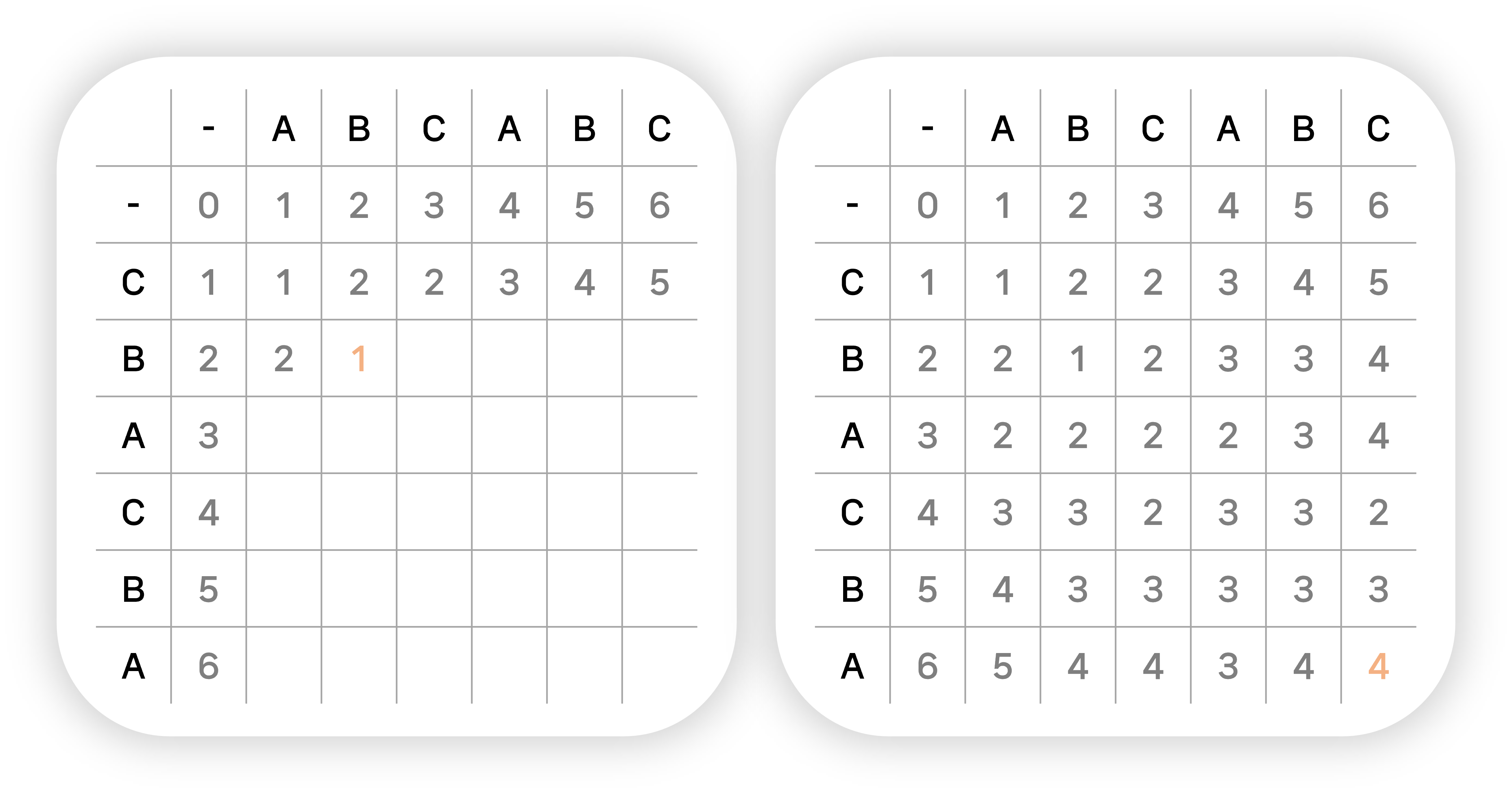
이후에 각 경우에 대해 문자열을 탐색하며 최소 편집 거리를 갱신한다. 이는 아래와 같은 방식으로 진행된다.

• 문자가 서로 동일할 경우
  - [ i - 1 ][ j - 1 ]의 편집거리로 저장한다.
• 문자가 서로 다른 경우
  - [ i - 1 ][ j ], [ i ][ j - 1 ], [ i - 1 ][ j - 1 ]중의 최솟값 +1 로 저장한다.

서로 동일한 경우에 대해 먼저 생각해보자. (i, j) 지점에서 문자가 동일하다면 (i - 1, j - 1) 지점에는 현 지점보다 길이가 하나 짧은 문자열에 대한 최소 편집 거리가 저장되어있다. 문자가 동일한 경우 편집할 필요가 없기 때문에 이전 편집 거리로 저장하게 된다.

반대로 다른 경우에는 3가지 편집 방법 중에 하나를 수행하여 문자를 같게 만들어줘야 한다. 이때 문자를 교체하는 연산이 [ i - 1 ][ j - 1 ] + 1 이고, 문자를 추가하는 연산이 [ i - 1 ][ j ] + 1, 문자를 삭제하는 연산이 [ i ][ j - 1 ] + 1에 해당한다. 최소 편집 거리이므로 이 중에 최솟값을 구하여 저장해준다.

문자열의 끝까지 이를 반복하여 수행한 이후의 가장 마지막 지점 값이 최소 편집 거리에 해당한다. 이에 대한 코드는 아래와 같다.

풀이 코드

#include <iostream>
#include <algorithm>
#include <string>
#include <vector>
using namespace std;

string X, Y;

int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
	
    // 입력값 입력받음
	cin >> X >> Y;
    // 2차원 배열로 사용할 vector 초기화
	vector<int> v(Y.length() + 1, 0);
	vector<vector<int>> result(X.length() + 1, v);
	
    // NULL에서부터의 최소 편집 거리 초기화
	for (int i = 0; i <= X.length(); i++) result[i][0] = i;
	for (int i = 0; i <= Y.length(); i++) result[0][i] = i;
	
    // 문자열을 탐색하며 최소 편집 거리 갱신
	for (int i = 1; i <= X.length(); i++) {
		for (int j = 1; j <= Y.length(); j++) {
			if (X[i - 1] == Y[j - 1]) result[i][j] = result[i - 1][j - 1];
			else result[i][j] = min(min(result[i][j - 1], result[i - 1][j]), result[i - 1][j - 1]) + 1;
		}
	}
    
    // 결과 출력
	cout << result[X.length()][Y.length()] << "\n";
	return 0;
}

결과