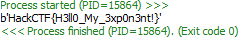2022년 코드게이트에 참여해보았다.
거기서 가장 인상깊었던 문제가 RSA 복호화 문제였는데, 결국 시간 내에 풀어내지 못하였다.
RSA에 대해 이론적으로만 알고 있던 것이 풀이에 실패한 원인인 것 같아, RSA에 관한 것들을 직접 실습해보면서 내용들을 정리해보려고 한다.

RSA

기본 원리

RSA는 두 소수 p와 q를 통해 N이라는 합성수를 구하는 것에서부터 시작한다.
그리고 (p-1)(q-1)을 통해 $\varphi(N)$을 구하고, $\varphi(N)$보다 작으며 서로소인 정수 e를 구한다.
이제 e의 $\varphi(N)$에 대한 모듈러 역수(modular inverse)인 임의의 d를 구하면 RSA의 준비가 모두 끝나게 된다.
( $ed\equiv1\ (mod\ \varphi(N))$ )

어떠한 평문 m에 대하여, m을 암호화한 암호문 c를 구하기 위한 식은 아래와 같다.

$c = m^e\ mod\ N$

그리고 이 암호문을 복호화하는 식은 아래와 같다.

$m = c^d\ mod\ N$

RSA 공격 기법 + write-up

$\varphi(N)$을 바로 알 수 있을 때

가장 기초가 되는 문제 상황이며, 너무 간단히 풀리기에 오히려 이런 상황이 주어지지 않는 경우가 더 많다.
N, p, q중 두 값 이상을 알고 있다면 $N=p\cdot q$를 통해 나머지 값들을 알 수 있으며, 알아낸 값들을 통하여 $\varphi(N)$를 구할 수 있다.
일반적으로 e값을 65537(=0x10001)로 설정해두거나 문제 상황에서 e를 알려주므로, 모듈러 역수 계산을 통해 d를 알아낼 수 있다.

간단한 워게임 문제를 풀어보며 간단하게 실습해보자.

문제 링크

위 사이트에서 RSA 문제를 살펴보자.
문제를 보면 p와 q, e, 그리고 c를 알려주고 있다.

p = 165500656692790480820099871308511495889550056248884963056391533737398719640777027536552348753003910353538512236389328276408434154714592616388810121411482595574799223632695324557638432891315001647024573557093357114908462069403023829967780936191142143068307535312844772151507357729244716123687935330409738850181
q = 122141438575770439104084639124669389798489623069980415671656975299923395151301777382093192959734330849008684250930530493655750402979451442939127736597078242925067195617957339753271262399847630938612930834827285581446954616798548644945058711157525778059878711651283927027641401287892466364366504983328484106481
e = 65537
c = 0x4730dcb8284416e44265091248de1ba51ce685ae5ff1276e263f72a1c90e34bcddc0ad1aa7757f1130c2f497b0629fb620e63b0b613ebe82c8b0a8d6f91a6652947f25c026307446cb7552e075e4754f1d60685a2b45e6238d3aca9934e47c0447e06d6162c91f912d14fb262ffce00e59fc8d04cbeb86cc5f087fbfe620b10e4d6a2c7ca9cb2ed315c31ee07b994b38c2827308c82de3b9ca7352505fe9b10a0ab4c81acc8334587f1277647509dca65001ad418f71e537d32bd71c10c89966b91a9426b440f3db5c52d4faf7440fbdae309bdd70769198e64995a6b3fdae748cc5db22dff8aa4fb235af657c96390d923a2b216dc34c07e28c588d8ef7c882

이제 $\varphi(N)$과 d만 결정해주면 복호화를 해줄 수 있다.
아래는 exploit code이다.

from Crypto.Util.number import *

p = 165500656692790480820099871308511495889550056248884963056391533737398719640777027536552348753003910353538512236389328276408434154714592616388810121411482595574799223632695324557638432891315001647024573557093357114908462069403023829967780936191142143068307535312844772151507357729244716123687935330409738850181
q = 122141438575770439104084639124669389798489623069980415671656975299923395151301777382093192959734330849008684250930530493655750402979451442939127736597078242925067195617957339753271262399847630938612930834827285581446954616798548644945058711157525778059878711651283927027641401287892466364366504983328484106481
e = 65537
c = 0x4730dcb8284416e44265091248de1ba51ce685ae5ff1276e263f72a1c90e34bcddc0ad1aa7757f1130c2f497b0629fb620e63b0b613ebe82c8b0a8d6f91a6652947f25c026307446cb7552e075e4754f1d60685a2b45e6238d3aca9934e47c0447e06d6162c91f912d14fb262ffce00e59fc8d04cbeb86cc5f087fbfe620b10e4d6a2c7ca9cb2ed315c31ee07b994b38c2827308c82de3b9ca7352505fe9b10a0ab4c81acc8334587f1277647509dca65001ad418f71e537d32bd71c10c89966b91a9426b440f3db5c52d4faf7440fbdae309bdd70769198e64995a6b3fdae748cc5db22dff8aa4fb235af657c96390d923a2b216dc34c07e28c588d8ef7c882

phi = (p-1)*(q-1)
d = inverse(e, phi)

m = pow(c, d, p*q)

print(long_to_bytes(m))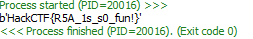

N이 충분히 작을 때

같은 사이트의 RSA2 문제를 살펴보자.

(n, c) = 
675517326695494061190287679557796696358902817969424171685361,
0xe3712876ea77c308083ef596a32c5ce2d7edf22abbc58657e

위와 같이 N과 c가 주어져있으며, p와 q는 알려주지 않는 경우가 대부분의 RSA 복호화 문제 상황이다.
그런데 지금 N이 겨우 60자리 수임을 볼 수 있다.
(60자리의 합성수는 분명 큰 수이지만, RSA에서는 굉장히 작은 수로 취급한다.)

이렇게 N이 작은 경우에는 단순한 소인수 분해만으로 p와 q를 얻어낼 수 있다.

factordb라는 사이트는 전세계의 사람들이 기여할 수 있는 소인수 보관 DB이다.
https://www.factordb.com/

위 사이트에 N의 값을 검색했을 때, 이미 알려진 N이었을 경우 p와 q를 곧바로 얻어낼 수 있다.
얻어낸 뒤에는 위에서 했던 대로 d를 구하여 c를 복호화하면 된다.

그런데 문제를 풀다보면 N이 알려져있지 않은 경우가 더 많다는 것을 알 수 있다.

이 경우 다양한 소인수 분해 툴을 통해 p와 q를 얻어내면 된다.
(이 방법은 N이 충분히 작을 때에만 시도해야 한다!)

위 문제에서는 N이 factordb에 기록된 값이었으므로, p와 q를 바로 얻어낼 수 있었다.

p = 804811499343607200702893651293
q = 839348502408870119614692320677

그런데, 이 문제에서는 e값을 알려주지 않고 있다.

e는 앞서 말했듯 보통 65537로 주어지며, 간혹 3으로 주어지기도 한다.

이 문제는 다행히 65537로 주어져있었다.
아래는 exploit code이다.

from Crypto.Util.number import *

n, c = 675517326695494061190287679557796696358902817969424171685361, 0xe3712876ea77c308083ef596a32c5ce2d7edf22abbc58657e

p = 804811499343607200702893651293
q = 839348502408870119614692320677

phi = (p-1)*(q-1)

d = inverse(65537, phi)

print(long_to_bytes(pow(c, d, p*q)))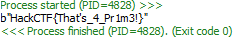

N이 충분히 크고, e가 3일 때

같은 사이트의 RSA3 문제는 다음과 같은 상황을 제시하고 있다.

n = 10283681839193276126097189449431804469761940095295471888398234447479454966284763902940257262270896218602885591849219329295416054197234326881779747263501982465102957508563705432633950651360492963151374387619070656704554971992649022858286686244477458518219811343940208016922937570643216329114427596008380607613093481777894261584227765149699743645734317383348201997748556656749211035951710759363655486663011079526697122026161182876988679088458171192764980121987583057238040415225285169219391637708267493561674900564748140379192079752942242600521017002960185256025253900075152690586476143729320416895984549165574371936823
c = 0x5c93ba85692a8b3981a5d47be0e80d129b8a2f6cf4dc134547aa7e1620f6691513b1dc1d69e085c39e261c2b49026436bb243dba70a86f7fcd1a3a7e6b0f0ecfac015becad0a76e9cf208d5d31e2b4865
e = 3

$c = m^e\ mod\ N$이므로, 어떤 자연수 $k$에 대하여 $m^e-c=k\cdot N$으로 바꾸어쓸 수 있다.
결국 $m=(k\cdot N + c)^{1/e}$라고 정리할 수 있는데, 평문 m은 정수의 형태여야 하므로 좌항의 값 또한 정수가 되어야만 한다.

그런데 이 k를 찾아내는 브루트 포스 코드를 작성하기에는, 코드의 작업 시간이 매우 오래 걸릴 수 있다는 것은 쉽게 알아낼 수 있다.
따라서 위의 아이디어를 약간 수정한 알고리즘이 필요하다.

만일 N이 너무나도 커서, $m^e$마저도 N보다 작다고 가정해보자.
그렇다면 결국 $c = m^e$가 성립된다.
즉, 단순한 e제곱근을 계산하는 것만으로도 복호화가 진행될 수 있다는 것이다.

이 방법을 이용한 exploit code는 다음과 같다.

from Crypto.Util.number import *
from gmpy2 import *

n =10283681839193276126097189449431804469761940095295471888398234447479454966284763902940257262270896218602885591849219329295416054197234326881779747263501982465102957508563705432633950651360492963151374387619070656704554971992649022858286686244477458518219811343940208016922937570643216329114427596008380607613093481777894261584227765149699743645734317383348201997748556656749211035951710759363655486663011079526697122026161182876988679088458171192764980121987583057238040415225285169219391637708267493561674900564748140379192079752942242600521017002960185256025253900075152690586476143729320416895984549165574371936823
c =0x5c93ba85692a8b3981a5d47be0e80d129b8a2f6cf4dc134547aa7e1620f6691513b1dc1d69e085c39e261c2b49026436bb243dba70a86f7fcd1a3a7e6b0f0ecfac015becad0a76e9cf208d5d31e2b4865
e = 3

k = 1

with local_context() as lcx:
    lcx.precision = 215
    print(long_to_bytes(int(cbrt(c))))

cbrt와 local_context는 모두 gmpy2에 정의되어있으며, 세제곱근을 구하는 함수 cbrt(n)의 정확도는 precision에 의해 결정된다.