백준 10828,11866,1654

문제 10828번

소스코드

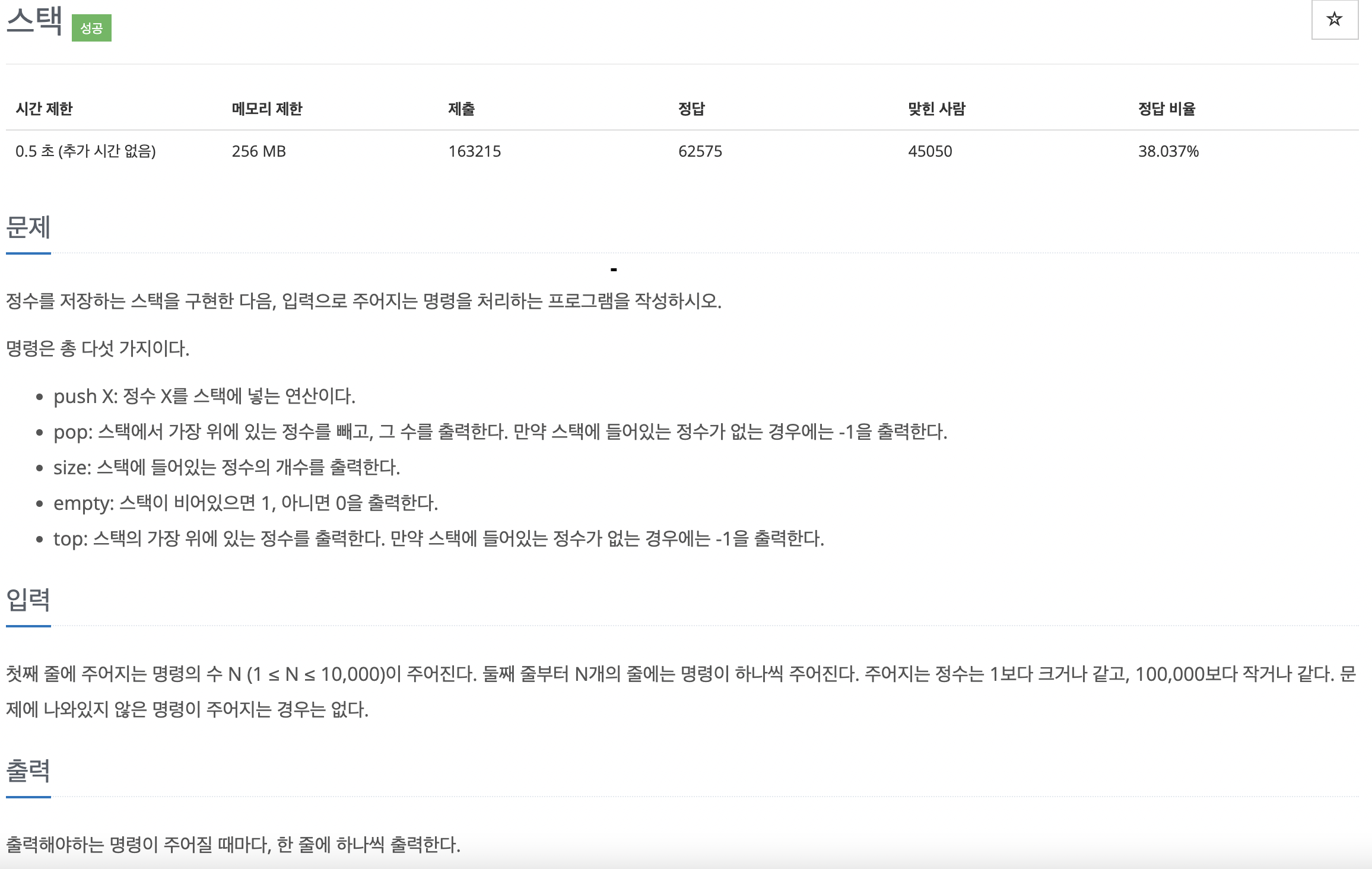
import java.io.*;
import java.util.*;
public class boj10828 {
    public static void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();
        Stack stack = new Stack();
        int N = Integer.parseInt(br.readLine());
        for (int i = 0; i < N; i++) {
            String[] input = br.readLine().split(" ");
            String name = input[0];
            int num =-1;
            if(input.length != 1){
                num = Integer.parseInt(input[1]);
            }
            if(name.equals("push")){
                stack.push(num);
            }else if(name.equals("pop")){
                if(stack.isEmpty()){
                    sb.append(-1 + "\n");
                }else{
                    sb.append(stack.pop() +" \n");
                }
            }else if(name.equals("size")){
                sb.append(stack.size() + "\n");
            }else if(name.equals("empty")){
                if(stack.isEmpty()){
                    sb.append(1 +"\n");
                }else{
                    sb.append(0 + "\n");
                }
            }else if(name.equals("top")){
                if(stack.isEmpty()){
                    sb.append(-1+ "\n");
                }else{
                    sb.append(stack.peek() + "\n");
                }
            }
        }
        System.out.println(sb);
    }
}

풀이 접근

1. 스택 선형 자료구조를 생각한다.
2. 입력을 받을 때 숫자를 같이 받을 떄를 예외처리한다.
3. 스택의 메소드를 이용하여 문제에서 주어진 상황을 해결한다.

문제 핵심

• 스택에 대한 기초적인 이해

문제 11866번

소스코드

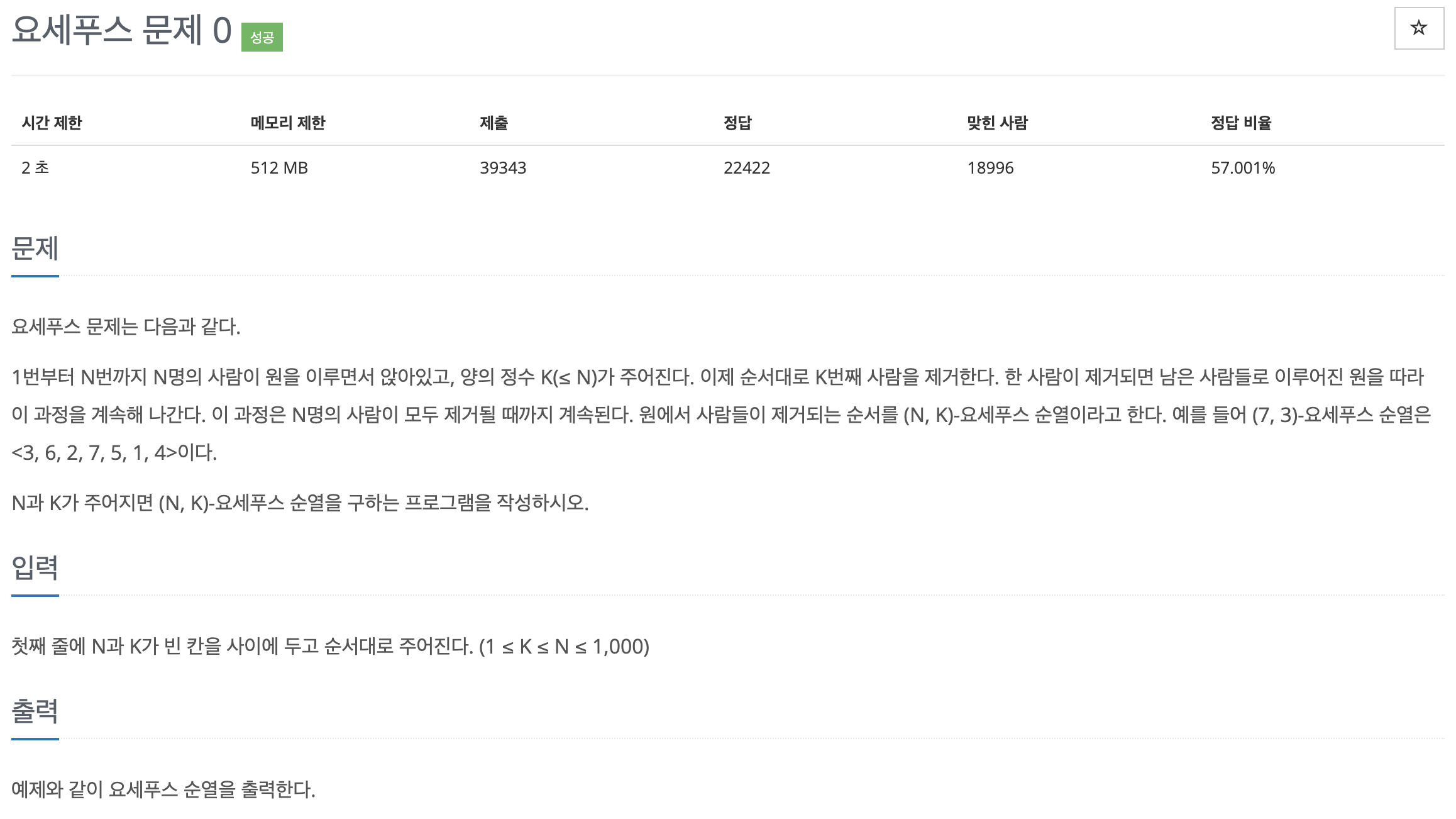
import java.io.*;
import java.util.*;
public class boj11866 {
    public static void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        StringBuilder sb = new StringBuilder();
        Queue qu = new LinkedList();
        int n = Integer.parseInt(st.nextToken());
        int k = Integer.parseInt(st.nextToken());
        for (int i = 1; i <= n; i++) {
            qu.add(i);
        }
        sb.append("<");
        while(!qu.isEmpty()){
            if(qu.size() ==1){
                sb.append(qu.poll() + ">");
            }else{
                for (int i = 0; i < k-1; i++) {
                    qu.add(qu.remove());
                }
                sb.append(qu.poll() + ", ");
            }
        }
        System.out.println(sb);
    }
}

풀이 접근

1. 요세푸스 순열에 대해 이해한다.
2. 해당 순열을 해결하기 위해서 자료구조 Queue를 사용한다.
3. queue메소드들을 통해 나머지 조건을 만족시킨다.

문제 핵심

• 요세푸스 순열에 대한 이해
• Queue 자료구조에 대한 이해

문제 1654번

소스코드

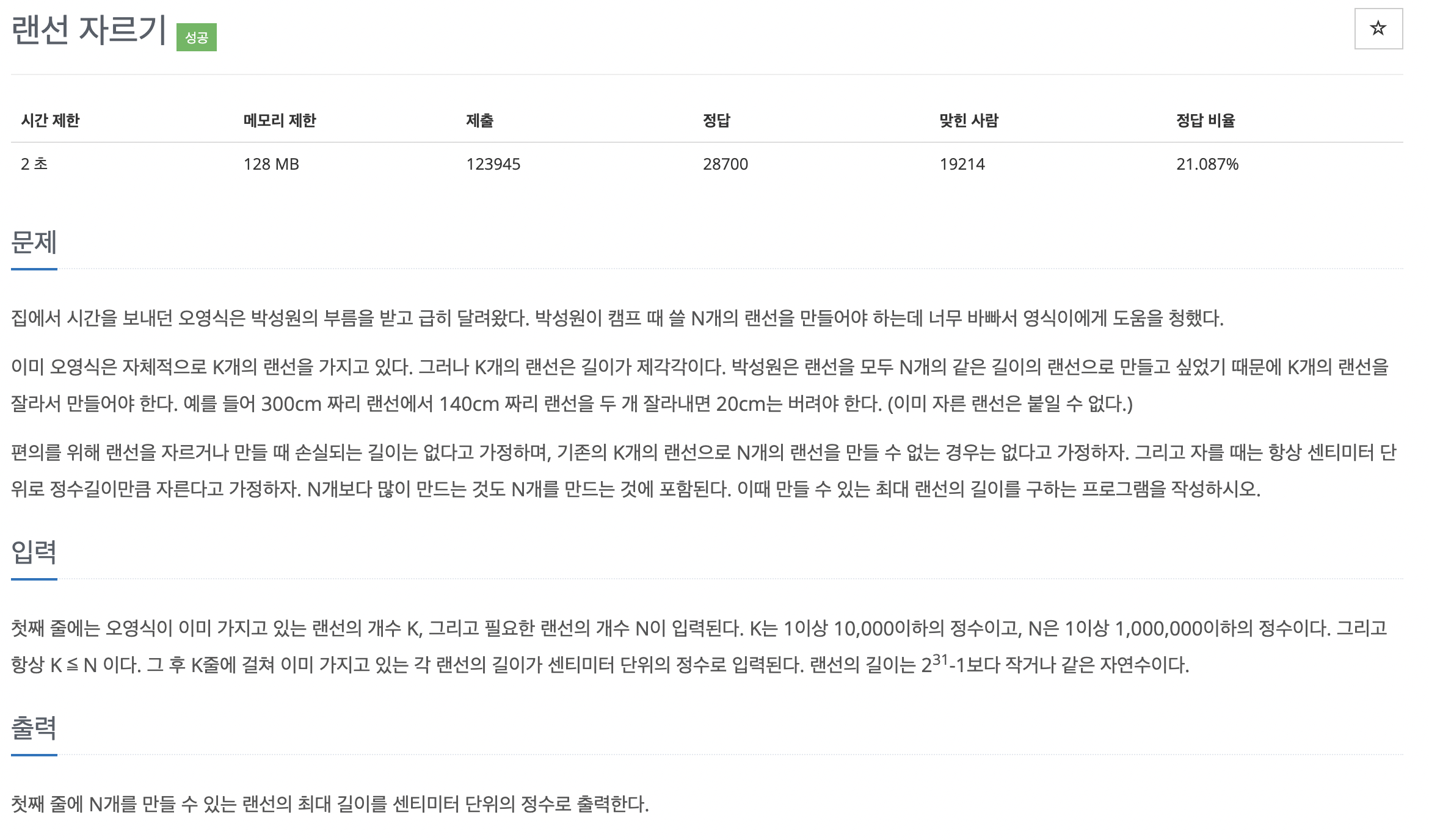
import java.io.*;
import java.util.*;
public class boj1654 {
    public static void search (int[] arr1, int a,int n){
        long first = 1;
        long last = a;
        long mid =0;
        while(first <= last) {
            mid = (first + last) / 2;
            int cnt = 0;
            for (int i = 0; i < arr1.length; i++) {
                cnt += arr1[i]/mid;
            }
            if(cnt<n){
                last = mid -1;
            }else{
                first = mid +1;
            }
        }
        System.out.println(last);
    }
    public static void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int k = Integer.parseInt(st.nextToken());
        int n = Integer.parseInt(st.nextToken());
        int[] arr = new int[k];
        for (int i = 0; i < k; i++) {
            arr[i] = Integer.parseInt(br.readLine());
        }
        Arrays.sort(arr);
        search(arr, arr[k-1], n);
    }
}

풀이 접근

1. 처음에는 배열 수의 합을 n의 수로 나눈 평균을 기준으로 반복문 탐색으로 찾았다.

• 시간초과

2. 탐색에 걸리는 시간을 줄이기 위해 이분탐색법을 사용한다.

문제 핵심

• 문제에서 정답으로 2^31 -1 까지 가능하다고 했음으로 long 변수 타입을 사용해야 한다.
• 시간 복잡도를 줄이는 방법을 생각한다.