배열의 성질
- O(1)에 k번째 원소를 확인/변경 가능
- 추가적으로 소모되는 메모리의 양(오버헤드)가 거의 없음
- Cache hit rate가 높음
- 메모리 상에 연속한 구간을 잡아야해서 할당에 제약이 걸림
기능과 구현
- 임의의 위치에 있는 원소를 확인/변경 = O(1)
- 원소를 끝에 추가 = O(1)
- 마지막 원소를 제거 = O(1)
- 임의의 위치에 원소를 추가/임의 위치의 원소 제거 = O(N)
// 1. 임의의 위치에 있는 원소를 확인/변경 = O(1)
// 확인
const element = arr[index];
// 변경
arr[index] = newValue;
// 2. 원소를 끝에 추가 = O(1)
arr.push(newElement);
// 3. 마지막 원소를 제거 = O(1)
arr.pop();
// 추가로 JS는 shift, unshift를 통해 첫번째 원소를 추가/제거도 가능하다 = O(N)
arr.shift()
arr.unshift()
// 4. 임의의 위치에 원소를 추가/임의 위치의 원소 제거 = O(N)
// 추가
arr.splice(index, 0, newElement);
// 제거
arr.splice(index, 1);https://youtu.be/mBeyFsHqzHg?si=ms5wKUyP9_693Kr6
영상 중 17분30초에 좋은 예시가 나온다. 다시 한번 볼만한 부분인것 같다.
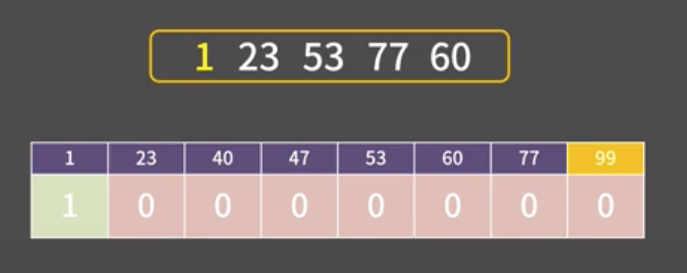
문제에서 만약 모든 수를 하나하나 쌍으로 검사하여 100이 되는 수를 찾는다면
시간복잡도는 모든 수를 검사하는 O(N)이 걸리고 이 과정을 N번을 검사하니 O(N^2)이 된다.
But, 이 방법을 사용하지 않고 한번만 검사하여 O(N) 걸리는 방법이 있는데
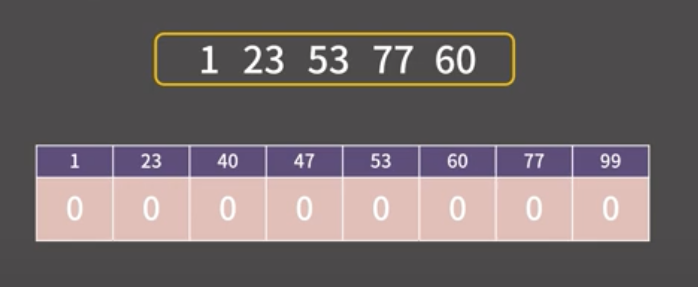
- 위 예시처럼 arr[1~100]까지 인덱스의 값을 0으로 설정하고 만든다
- 첫번째 1과 더해서 100이 되는 수, 99가 이전에 등장했는지 검사
- 이전에 99가 나오지 않았다면 arr[1]++, 즉 1을 더한다.
위 방법을 반복하면 77을 검사할때 100이 되기 위한 23은 등장하게 되었으니 O(N) 만으로 찾을수 있게된다
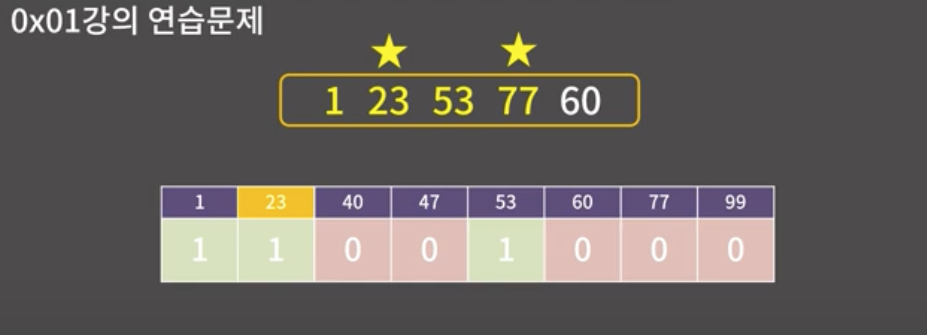
배열문제는 배열을 이용하여 풀 수 있는 문제가 꽤나 있었던 것 같다. 백준의 알파벳 문제가 가장 기본적인 예시
또한 배열문제에서 시간 제한이 있을 때 새로운 배열을 생성 후 최소한의 시간을 이용하여 푸는 생각을 하는 습관을 들이는것도 중요하다 느낌

