재귀
재귀는 하나의 함수에서 자기 자신을 다시 호출해 작업을 수행하는 알고리즘
수학적 귀납법

재귀에서는 수학적 귀납법으로 생각하여야한다.
k번 도미노가 쓰러지면 k+1도 쓰러진다
k+1번 도미노가 쓰러지면 k+2도 쓰러진다.
절차지향적 사고

func1(3)을 실행했을 때 3 2 1 이 출력되는것을 알 수있다.
귀납적 사고

여기서 만약 func1(k)를 호출하게 되면 k k-1 k-2 ... 1을 출력하게 된다..
조금 어렵다고 생각이 드는데 만약 func(k+1)을 호출하면
k+1을 출력을 하고 func(k)가 출력이 되니,
여기서 k는 func(k) = k k-1 k-2 ...1 이므로
func(k+1)의 순서는 k+1 k k-1 ... 1 이렇게 된다.
이 조건이 맞으니 위 함수는 n부터 1까지 귀납적 함수라는것을 알 수 있다.
재귀 함수의 조건
올바른 재귀함수는 반드시 특정 입력에 대해서는 자기 자신을 호출하지 않고 종료 되어야 함(Base Condition) 모든 입력은 base condition으로 수렴해야 함
한마디로 중단문(종료문)이 있어야 된다.
만약 재귀를 탈출하지 못한다면 무한루프가 돌아가고 결국엔 런타임에러가 발생한다.
재귀에 대한 정보 1
- 함수의 인자로 어떤 것을 받고 어디까지 계산한 후 자기 자신에게 넘겨줄지 명확하게 정해야 함
- 모든 재귀 함수는 반복문만으로 동일한 동작을 하는 함수를 만들 수 잇음
- 재귀는 반복문으로 구현했을 때에 비해 코드가 간결하지만 메모리/시간에서는 손해를 봄
JS로 코테를 보는데 메모리/시간 때문에 조금 걱정이다. 하지만 구글링을 하면 사람들이 사용하는 대안이 있어 좀 하면 될듯
재귀에 대한 정보 2
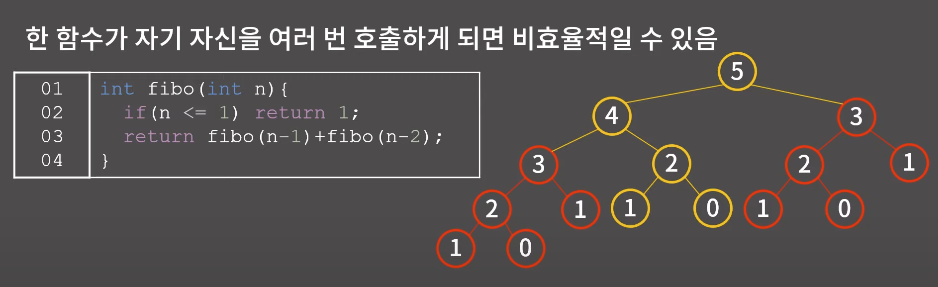
피보나치 함수의 재귀 호출을 보면, 이미 호출했던 함수를 또 호출하여 계산하게 되어 시간복잡도가 매우 올라간다.
이와 같이 한 함수가 자신을 여러 번 호출하게 되면 비효율적이다.
시간복잡도를 해결하려면 DP를 이용해 해결 할 수있다고한다. 아마 점화식? 으로 풀지 않을까
재귀에 대한 정보 3
재귀함수가 자기 자신을 부를 때 스택 영역에 계속 누적이 됨

우리는 문제를 풀 때 메모리제한이 있다.
위 다섯가지의 종류가 메모리를 사용하게 되는데 그 중 우리가 사용하는 스택은
일부 컴파일 환경에서는 1MB로 제한이 되어있다고 한다. (백준은 제한이 없다. 다른 코테사이트에는 있을수도있음)
스택에 10만번 정도 들어가게되면 1MB가 넘어가버리니 메모리 제한이 걸린다면 어쩔수없이 반복문을 이용해 풀어야한다.
연습문제 - 하노이탑

하노이문제도 재귀를 대표하는 문제이다.
자신보다 큰 수는 위로 올라 올 수 없다.
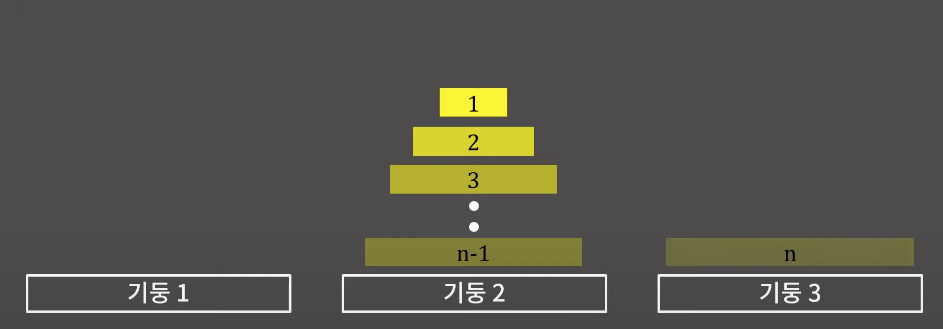
n의 원판을 기준으로 생각하면 n의 원판이 기둥3의 제일 마지막에 와야한다.
그러니 n-1~1 까지의 원판은 기둥2로 갔다가 기둥3으로 간다면 하노이탑이 완성이된다.

과정을 보면 n-1개의 원판을 원하는 곳으로 옮길 수만 있다면, n개의 원판을 처리 할 수 있다.
요약하자면,
- n-1개의 원판을 기둥 1에서 기둥 2로 옮긴다.
- n번 원판을 기둥 1에서 기둥 3으로 옮긴다.
- n-1개의 원판을 기둥 2에서 기둥 3으로 옮긴다.
-> 원판이 n-1개일 때 옮길 수 있으먄 원판이 n개일 때에도 옮길 수 있다.
원판이 1개일 때 원판을 내가 원하는 곳으로 옮길 수 있다.
원판이 k개 일 때 옮길 수 있으면 원판이 k+1개일 때에도 옮길 수 있다.
1. 함수의 정의
function(a,b,n)
// 원판 n개를 a번 기둥에서 b번 기둥으로 옮기는 방법을 출력하는 함수2. base condtion
if(n===1){
//a 기둥에서 b기둥으로 이동
}3. 재귀식
-
n-1개의 원판을 기둥 a에서 6-a-b로 옮긴다.
6-a-b로 하는 이유는 기둥이 1,2,3번이 있는데 a,b가 각각 1,2 일 경우 6-a-b 3이되고 2,3일 경우 1이 된다.
이건 비어있는 기둥으로 이동 하기 위해 저 식을 씀
function(a, 6-a-b, n-1)
-
n번 원판을 기둥 a에서 b로 옮긴다.
-
n-1개의 원판을 기둥 6-a-b에서 기둥 b로 옮긴다.

