[알고리즘] 힙(Heap)

Ne5s·2022년 9월 28일

알고리즘 정리

목록 보기

5/6

힙(Heap)

힙은 자료구조이고 트리의 일종입니다. 기본적으로 트리이므로 트리에 대해 적용되는 것은 일반적으로 힙에도 적용됩니다.
힙을 이용해서 우선순위 큐를 이용할 수 있습니다. 그렇기 때문에 배울 필요가 있었습니다.
힙에도 종류가 많습니다. 피보나치 힙, 레오나르도 힙, Soft heap, Leftist heap 등이 있습니다. 우리가 주로 다루게 될 것은 이진 힙입니다. 여기엔 최소 힙과 최대 힙이 있습니다.

<힙의 특징>

힙에서 부모는 최대 두개의 자식 노드를 갖습니다.
이진 힙은 언제나 가능한 가장 적은 공간을 차지합니다. 다음 레벨로 내려가기 전에 모든 왼쪽/오른쪽 노드가 다 채워집니다.
한 줄에서는 왼쪽 자식이 언제나 먼저 채워집니다.
형제 노드 사이에는 어느 관계도 존재하지 않는다.

이진탐색트리와 힙의 차이

이진탐색트리와 비슷하지만 힙에는 왼쪽과 오른쪽에 순서가 존재하지 않습니다.
아래 그림은 최대힙의 예시입니다. 단순히 자식이 부모보다 작을 뿐입니다.

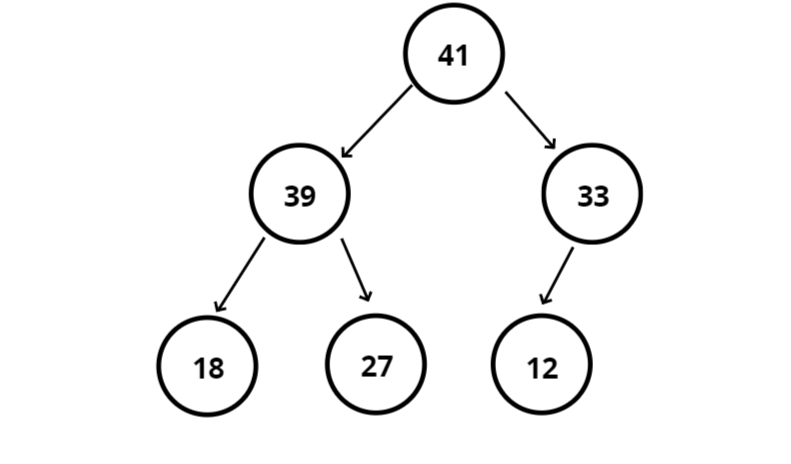
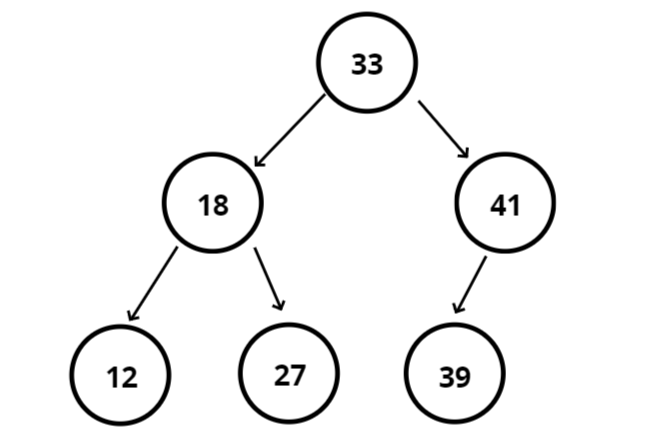
아래 그림은 이진 탐색 트리입니다.
자식 노드 중 왼쪽은 부모 노드보다 작고 오른쪽은 부모 노드보다 큽니다.

파이썬에서의 힙

파이썬에서는 힙 기능을 위해 heapq라는 표준 라이브러리를 지원한다.
heapq는 다익스트라 최단 경로 알고리즘을 포함해 다양한 알고리즘에서 우선순위 큐 기능을 구현하고자 할 때 사용된다.
PriorityQueue 라이브러리도 이용 가능하다고 하는데, heapq가 더 빠르므로 heapq를 주로 사용한다고 한다.

heapq 모듈은 이진 트리(binary tree) 기반의 최소 힙(Min Heap, 부모 노드가 자식 노드보다 항상 작은 값을 가짐) 자료구조 만을 제공한다.
내부적으로는 인덱스 0에서 시작해 k번째 원소가 항상 자식 원소들(2k+1, 2k+2) 보다 작거나 같은 최소 힙의 형태로 정렬된다.
이 것을 이용하면 단순히 원소를 힙에 전부 넣었다가 빼는 것만으로도 시간 복잡도 O(NlogN)에 오름차순 정렬이 완료된다.

힙에 원소를 삽입할 때는 heapq.heappush() 메서드를 이용하고, 힙에서 원소를 꺼내고자 할 때는 heapq.heappop() 메서드를 이용한다.

heapq 모듈은 파이썬의 보통 리스트를 마치 최소 힙처럼 다룰 수 있도록 도와줍니다.
그렇기 때문에 빈 리스트를 생성해놓은 다음 heapq 모듈의 함수를 호출할 때마다 이 리스트를 인자로 넘겨야 합니다. 다시말해, heapq 모듈을 통해서 원소를 추가하거나 삭제한 리스트가 최소 힙이 되는 것입니다.

예제 1(오름차순 정렬)

힙 정렬(Heap Sort)를 heapq로 구현하는 예제이다.
heappush() 함수의 첫번째 인자는 원소를 추가할 대상 리스트,
두번째 인자는 추가할 원소이다.
heappush(), heappop() 함수는 O(logn)의 시간복잡도를 가집니다.

import heapq

def heapsort(iterable):
	h = []
    result = []
    # 모든 원소를 차례대로 힙에 삽입
    for value in iterable:
    	heapq.heappush(h, value)
    # 힙에 삽입된 모든 원소를 차례대로 꺼내어 담기
    for i in range(len(h)):
    	result.append(heapq.heappop(h))
    return result
    
result = heapsort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0])
print(result)

예제 2(내림차순 정렬)

파이썬에서는 최대 힙(Max Heap, 부모 노드가 자식 노드보다 항상 큰 값을 가짐)을 제공하지 않는다. 따라서 최대 힙을 구현할 때는 최소 힙을 이용하는 방식과 비슷하게 작성하고 원소의 부호를 임시로 변경하는 방식을 사용한다.
힙에 원소를 삽입하기 전에 잠시 부호를 반대로 바꾸었다가, 힙에서 원소를 꺼낸 뒤에 다시 원소의 부호를 바꾸면 된다.

import heapq

def heapsort(iterable):
	h = []
    result = []
    # 모든 원소를 차례대로 힙에 삽입
    for value in iterable:
    	heapq.heappush(h, -value)
    # 힙에 삽입된 모든 원소를 차례대로 꺼내어 담기
    for i in range(len(h)):
    	result.append(-heapq.heappop(h))
    return result
    
result = heapsort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0])
print(result)

예제 3(기존 리스트를 힙으로 변환)

heapify() 함수에 리스트를 인자로 넘기면 리스트 내부의 원소들이 힙 구조에 맞게 재배치되며 최소값이 0번째 index에 위치됩니다.
결과적으로는 비어있는 리스트를 생성하고 heappush()로 원소를 하나씩 넣어준 효과와 같습니다.
시간복잡도는 리스트의 원소수인 n에 비례하며 O(n)입니다.

from heapq import heapify

li = [9, 0, 4, 2, 3, 8]
heapify(li)
print(li)

heapify() 함수는 새로운 리스트를 반환하는 것이 아니라 리스트를 직접 변경하므로 원본 리스트를 보존하고자 할 경우에는 아래와 같이 사용해야 합니다.

li = [9, 0, 4, 2, 3, 8]

toHeap = li[:]
heapify(toHeap)

print(li)
print(toHeap)

예제 4(n번째 최소값/최대값)

<직접 구현>

from heapq import heapify, heappop
def nth_smallest(nums, n):
    heapify(nums)

    nth_min = None
    for _ in range(n):
        nth_min = heappop(nums)

    return nth_min

<라이브러리의 함수 이용>
nsmallest() 함수는 주어진 리스트에서 가장 작은 n개의 값을 담은 리스트를 반환한다.
그렇기 때문에 함수의 결과의 마지막 인덱스가 n 번째 작은 값이 된다.
nlargest()함수도 위와 마찬가지로 가장 큰 n개의 값을 담은 리스트를 반환하므로,
마지막 인덱스 값이 n 번째 큰 값이 된다.

from heapq import nsmallest

nsmallest(3, [4, 1, 7, 3, 8, 5])[-1]
#-------------------------------------
from heapq import nlargest

nlargest(3, [4, 1, 7, 3, 8, 5])[-1]