[algorithm] 자바스크립트 빅오 표기법 (Big-O)

chaeyeon·2023년 1월 18일

알고리즘을 구현하기 전에 알고리즘이 얼마나 효과적인지 분석하는 법을 이해해야 한다.
알고리즘을 구현할 때 빅오 표기법이 해당 알고리즘이 얼마나 효율적인지를 나타내기 때문에 빅오 표기법은 중요하다.
효율적인 방법을 고민한다는 것은 시간 복잡도를 고민한다는 것과 같은 말이다.
빅오 표기법은 알고리즘의 최악의 경우 복잡도를 측정하며 알고리즘의 효율성을 나타내는 표기법이다.

Time Complexity (시간 복잡도)

문제를 해결하는데 걸리는 시간과 입력의 관계를 가리킨다.
즉, 입력값에 따라 연산을 실행할 때, 연산 횟수에 비해 얼마만큼의 시간이 걸리는가를 의미한다.
시간복잡도를 고민한다는 것은 입력값이 커짐에 따라 증가하는 시간을 최소화한 알고리즘을 만들었다는 의미이기도 한다.
시간복잡도는 Big-o 표기법을 사용해 나타낼 수 있다.

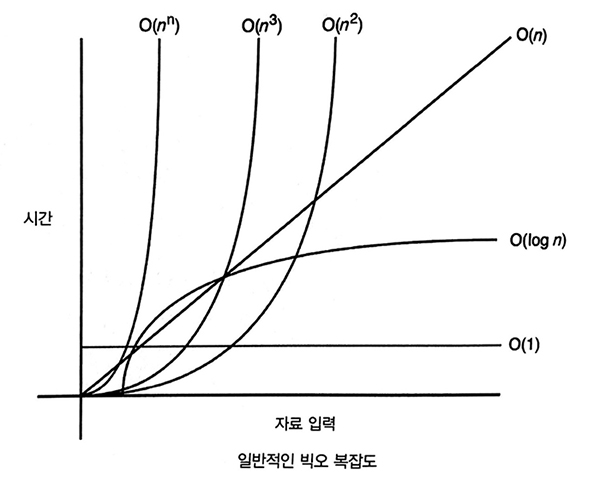
출처 : 자바스크립트로하는 자료 구조와 알고리즘

*시간복잡도 순서 : 𝑂(1) < 𝑂(log n) < 𝑂(n) < 𝑂(n log n) < 𝑂(n²) < 𝑂(n³) < 𝑂(2ⁿ) < 𝑂(n!)

알고리즘 분석 시 가장 자주 등장하는 유형

표기법	명칭
O(1)	상수
O(n)	선형
O(n²)	2차
O(log₂ n)	로그
O(n log₂ n)	다형 로그
O(n^c)	고차
O(2ⁿ)	지수

O 표기법 이해

알고리즘의 효율은 어떻게 측정할 수 있을까?
보통 CPU(소요 시간), 메모리, 디스크, 네트워크의 사용량을 생각할 수 있는데, 그중 O 표기법은 CPU 사용량을 대상으로 한다.

1. O(1)

입력값이 증가하더라도 시간은 변하지 않는다. 따라서 O(1)을 상수 시간이라고 부른다.

입력값의 크기와 관계없이 즉시 출력값을 얻을 수 있다.
배열의 항목을 인덱스를 사용해 접근하는 경우를 예로 들 수 있다.

// 예제 1
function O_1(arr, index) {
  return arr[index];
}
const arr = ['a', 'b', 'c', 'd', 'e'];
let index = 3;
console.log(O_1(arr, index)); // 'd'

// 예제 2
function increment(num) {
  return num++;
}
console.log(increment(99)); // 100

함수 실행시 걸리는 시간을 X라고 했을 때, 예제 1과에서 arr 배열의 개수가 늘어나거나 index의 값이 바뀌더라도 즉시 출력값을 얻을 수 있다.
예제 2또한 99를 다른 숫자로 바꾸어도 실행 시간은 여전히 X이다.
인자에 상관없이 함수의 성능은 달라지지 않기 때문에 일정한 O(1)의 복잡도를 갖는다.

2. O(n)

선형 복잡도라고 부르며, 입력값의 증가도에 따라 시간도 동일한 비율로 증가하는 것을 의미한다.

// 예제 3
function sequentialSearch(array, item) {
  for (let i = o; i < array.length; i++) {
    if (item === array[i]) {
      return i;
    }
  }
  return -1;
}
const arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
const item = 1;

예제 3에서 배열에서 item의 값과 같으면 그 즉시 함수를 종료한다.
만약 item이 1이라면 첫번째 루프 실행 시 곧바로 종료된다.
루프 반복시 드는 비용 : {1}, item = 10 → 총 {10}의 비용 발생 (1을 찾을때 보다 10배의 비용이 든다.)
(최악의 경우 → 값이 없어도 모든 루프를 돌고 -1을 리턴할 것이다.)
arr = [1... 1000], item = 1000 일때 드는 비용은 1000이다.

최악의 경우일 때, 크기가 1000이면 비용도 1000이 되므로 O(n)의 시간복잡도를 갖게 되는 것이다.

3. O(n²)

O(n²)은 2차 복잡도라고 부르며, 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미한다.

대표적으로 버블 정렬 알고리즘이 있다.

// 예제 4
function swap(array, index1, index2) {
  let aux = array[index1];
  array[index1] = array[index2];
  array[index2] = aux;
}

function bubbleSort(array) {
  let length = array.length;
  for (let i = 0; i < length; i++) {
    for (let j = 0; j < length - 1; j++) {
      if (array[j] > array[j + 1]) {
        swap(array, j, j + 1);
      }
    }
  }
}
const arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
bubbleSort(array);

크기가 10인 배열을 넣고 실행하면 총 비용은 100(10²) 이다.
크기가 100인 배열이면 총 비용은 10000(100²)이 된다.
입력값이 커질수록 실행 시간은 기하급수적으로 늘어난다.

* 단일 루프라면 O(n), 중첩 루프면 O(n²), 삼중 루프라면 복잡도는 O(n³)이 된다.

4. O(log₂ n)

입력값의 크기가 커질수록 실행 시간이 로그(log: 지수 함수의 역함수) 만큼 짧아지는 알고리즘
예를 들어 데이터가 10배가 되면, 처리 시간은 2배가 된다.
대표적으로는 이진 탐색이 있다.
재귀가 순기능으로 이루어지는 경우도 해당된다.

5. O(n log₂ n)

데이터가 많아질수록 처리시간이 로그(log) 배만큼 더 늘어나는 알고리즘
예를 들어 데이터가 10배가 되면, 처리 시간은 약 20배가 된다.
대표적으로는 병합 정렬, 퀵 정렬이 있다.

6. O(2ⁿ)

데이터량이 많아질수록 처리시간이 기하급수적으로 늘어나는 알고리즘
대표적으로 피보나치 수열이 있으며, 재귀가 역기능을 할 경우도 해당된다.

시간복잡도 줄이는 법

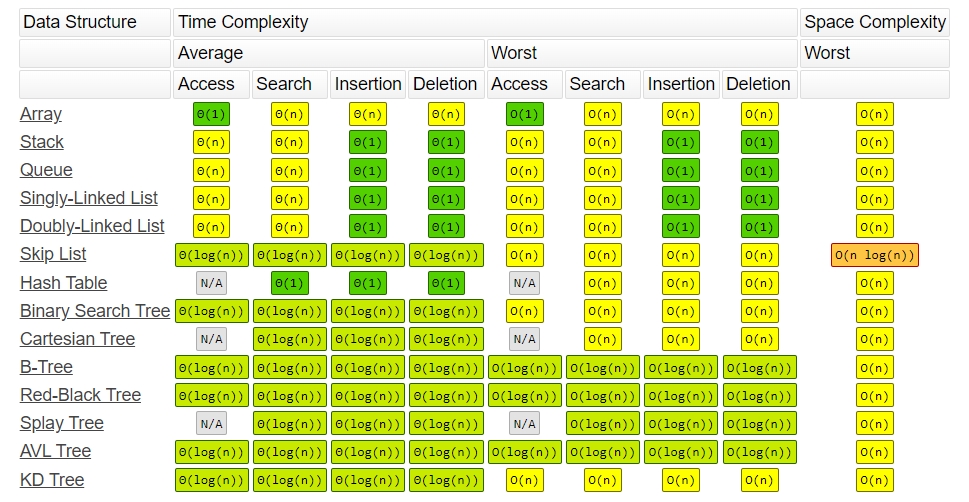
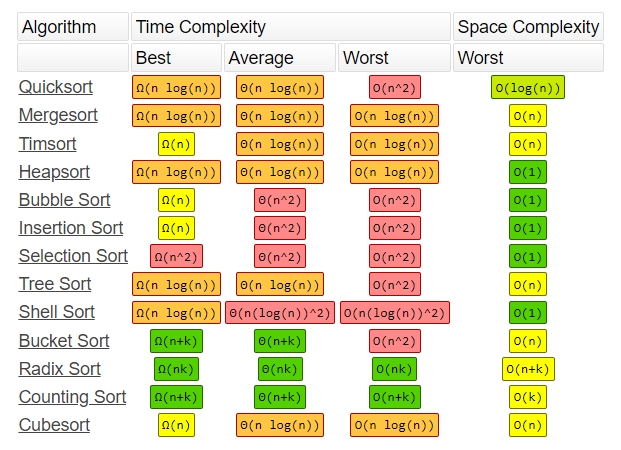
출처 : https://www.bigocheatsheet.com/

자료구조 및 알고리즘을 적절히 사용하여 시간복잡도를 줄이고 **반복문으로 인해 시간 복잡도가 기하급수적으로 증가 할 수 있으니 반복문 사용에 유의하도록 한다.**
위의 표를 참고하면 유명한 알고리즘이 어떤 시간 복잡도를 가지고 있는지 알 수 있다.
위에서 나오는 알고리즘 정도는 열심히 공부해야 겠다.

-참고