[알고리즘] 소수 구하기 - 에라토스테네스의 체

에라토스테네스의 체?

소수를 찾는 알고리즘이다.

알고리즘

1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
2. 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
   자기 자신을 제외한 2의 배수를 모두 지운다.
3. 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
   자기 자신을 제외한 3의 배수를 모두 지운다.
4. 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
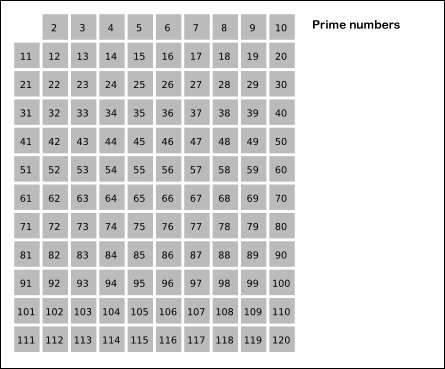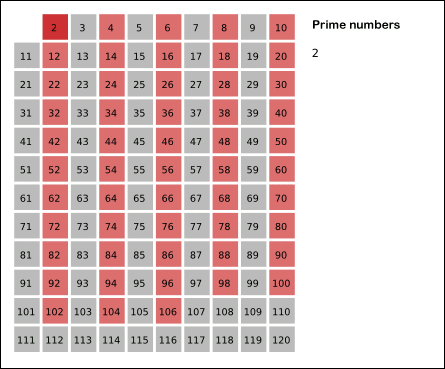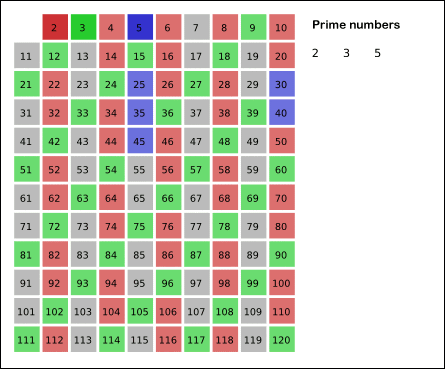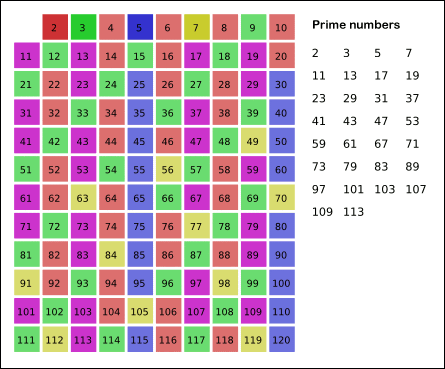
   자기 자신을 제외한 5의 배수를 모두 지운다.
5. 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
   자기 자신을 제외한 7의 배수를 모두 지운다.
6. 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다. (보라색)
   
   (출처 : 에라토스테네스의 체 - 위키백과)

코드 구현

public void Prime(int n) {
	boolean[] isPrime = new boolean[n+1];
    Arrays.fill(isPrime, true);
    
    // 소수는 true
    //0, 1은 소수가 아니므로 false
	isPrime[0] = false;
    isPrime[1] = false;
    
    for(int i = 2; i <= n; i++) {
    	if(isPrime[i]) { // i가 소수이면 i의 배수들을 모두 false로 바꿔준다.
       		for(int j = i*i; j <= n; j+=i) { 
            	isPrime[i] = false;
            }
         }
     }
       
}