문제 링크: https://school.programmers.co.kr/learn/courses/30/lessons/138475
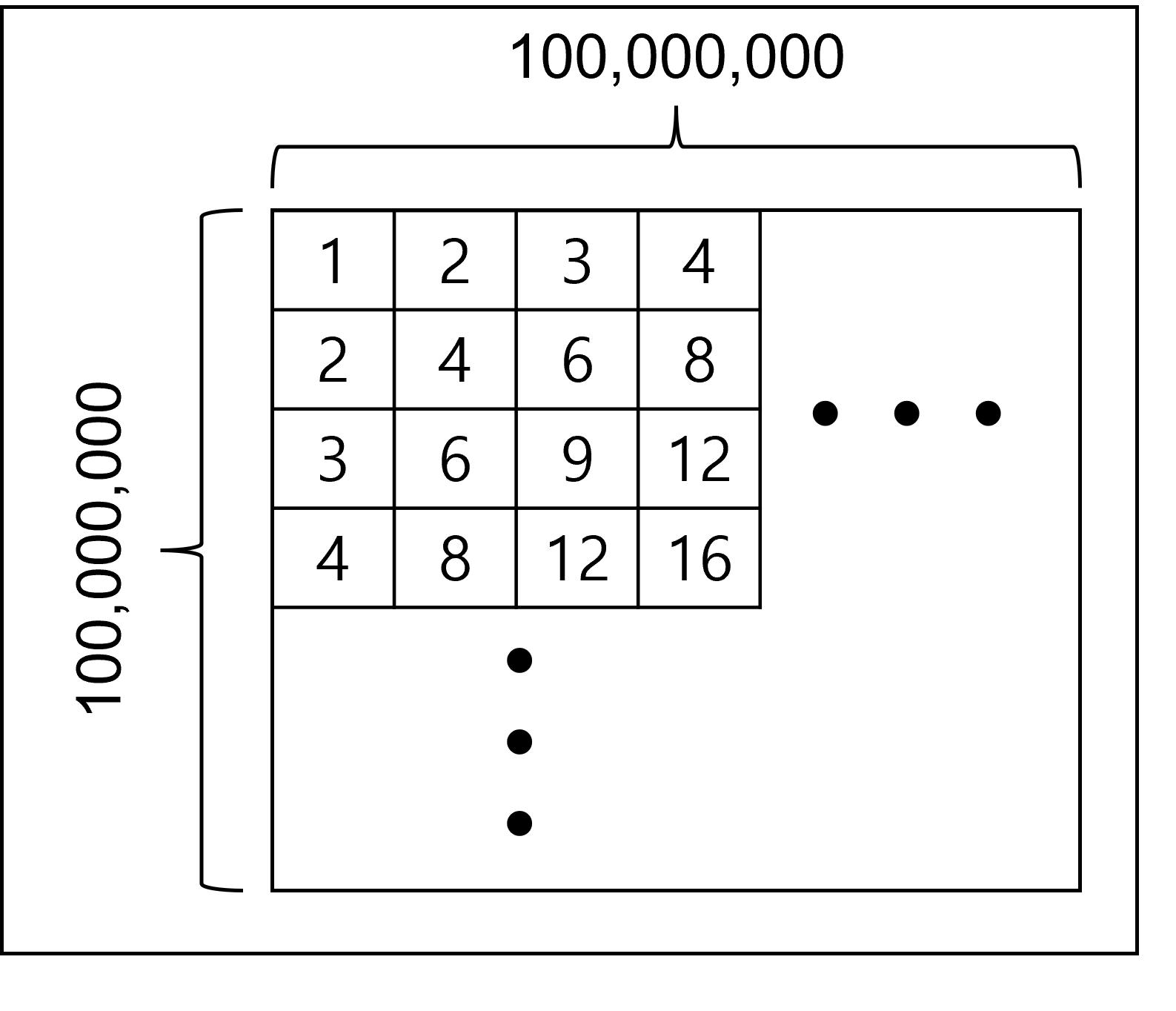
적당한 수 e를 먼저 정하여 알려주고 e 이하의 임의의 수 s를 여러 개 얘기합니다. 영우는 각 s에 대해서 s보다 크거나 같고 e 보다 작거나 같은 수 중에서 억억단에서 가장 많이 등장한 수를 답해야 합니다. 만약 가장 많이 등장한 수가 여러 개라면 그 중 가장 작은 수를 답해야 합니다.
제한 사항
- 1 ≤ e ≤ 5,000,000
- 1 ≤ starts의 길이 ≤ min {e,100,000}
- 1 ≤ starts의 원소 ≤ e
- starts에는 중복되는 원소가 존재하지 않습니다.
그렇다 제한 사항을 보면 알 수 있겠지만 제목만 억억단이지 e가 5백만으로 제한되어 있기 때문에 사실상 오백만오백만단이다.
이 문제가 3단계인 이유는 최적화된 약수 카운팅 방법 숙지와 약간의 메모이제이션이 필요하기 때문인 것 같다
생각보다 약수 카운팅 최적화가 어려운 부분이었는데
처음에는 아래와 같은 코드로 1부터 e까지의 약수를 계산했다.
def get_divisor(num):
cnt = 0
if num ** 0.5 == int(num ** 0.5):
cnt -= 1
for i in range(1, int(num ** 0.5)+1):
if num % i == 0:
cnt += 2
return cnt하지만 이렇게 약수를 카운팅하게 되면 O(n^3/2)으로 계산을 하게되고 약 5000000 * sqrt(5000000) = 100억번의 연산을 수행하게 됩니다. 그래서 시간 초과가 나오게 된다...(사실 100억번은 좀 과장된 거고 이거보단 적다)
1부터 e까지의 모든 수에 대한 약수를 구하는 문제의 특성 상 이보다 더 최적화하게 되면 아래와 같이 계산할 수 있다.
위 함수를 e번 호출하는 것 보다 아래의 2중 for문을 통해 divisor 리스트에 한번에 계산하는 것이 빠를 것 같지 않은가?
divisor = [1 for _ in range(e+1)]
for i in range(2, e+1):
for j in range(i, e+1, i):
divisor[j] += 1이 방법은 두 번째 for문에서 i의 배수에만 1을 더함으로써 횟수를 줄일 수 있었습니다. 연산의 수는 다음과 같은 급수로 표현할 수 있다.

이 급수의 합을 이용해 시간복잡도를 표시할 수 있는데 결과적으로 nlog(1+n/2)을 따른다. 따라서 O(nlogn)으로 볼 수 있다. 자세한 증명은 아래 링크에서 참고하자!
Referenced: https://suhak.tistory.com/261
그리고 약간의 메모이제이션을 이용하는데 필자는 시간과 공간 복잡도를 줄이기 위해 꼼수를 사용했고 다른 사람들은 그냥 divisor과 같은 크기의 메모 배열을 생성하고 O(1)의 복잡도로 계산된 약수에 대해 접근했다.
필자는 dict의 해시 테이블을 이용해 마찬가지로 O(1)의 복잡도로 약수에 접근했고 공간 복잡도는 훨씬 줄일 수 있었다. 하지만 계산하기 위해 starts 배열을 정렬해서 O(nlogn)만큼의 시간이 걸리긴 하지만 약수를 구하는 것으로도 많은 시간이 걸리기 때문에 크게 상관하지 않는다.
def solution(e, starts):
result = []
divisor = [1 for _ in range(e+1)]
memo = 0
starts_dict = {}
sorted_starts = sorted(starts)
for i in range(2, e+1):
for j in range(i, e+1, i):
divisor[j] += 1
for i in range(len(sorted_starts)):
if memo == 0:
max_index = divisor[sorted_starts[i]:].index(max(divisor[sorted_starts[i]:]))+sorted_starts[i]
starts_dict[sorted_starts[i]] = max_index
memo = max_index
else:
if sorted_starts[i] <= memo:
starts_dict[sorted_starts[i]] = memo
else:
memo = divisor[sorted_starts[i]:].index(max(divisor[sorted_starts[i]:]))+sorted_starts[i]
starts_dict[sorted_starts[i]] = memo
for s in starts:
result.append(starts_dict.get(s))
return result