알고리즘

주어진 출발 꼭짓점에서부터, 목표 꼭짓점까지 가는 최단 경로를 찾아내는 그래프 탐색 알고리즘 중 하나다익스트라 알고리즘은 시작 노드만을 지정하여 다른 모든 노드에 대한 최단 경로를 파악하지만,에이스타 알고리즘은 시작 노드 & 목적지 노드를 분명하게 지정또한 에이스타 알

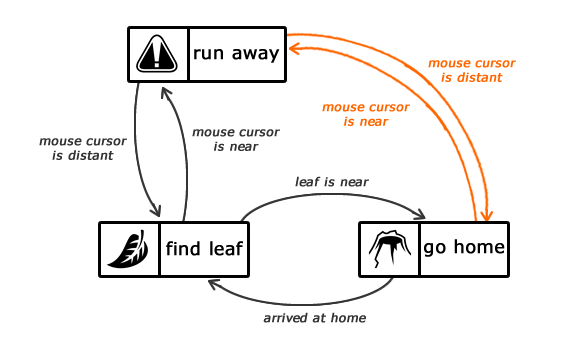
Finite-State Machine(유한 상태 머신) : Execution Flow를 표현하고 제어하기 위한 모델 특히 게임 내 AI를 구현할 때 좋음 여러 가지의 State들이 존재하며, 하나의 State만 활성화될 수 있기 때문에, 다른 Action을 취하기 위

백준을 풀다가 2609번, 최대공약수 / 최소공배수 구하는 알고리즘을 구현하는 것을 보았는데굳이 for문이나 while 돌려 가며 브루트 포스를 하고 싶지 않아서...더 빠른 방법이 있을까 하여 알고리즘을 찾아보았다.최대공약수 구할 땐, 유클리드 호제법을 이용한다.x,

소수를 찾는 데 for나 while문을 돌릴 수도 있다.그치만 귀찮기도 하고... 만약 여러 개의 소수를 찾아야 하는 경우, 시간복잡도는 O(n^2)이 든다.에라토스테네스의 체는, 여러 숫자에 대해 소수인지 아닌지를 판별해야 할 때 유용하다.시간복잡도도 O(n log