멀쩡한 사각형

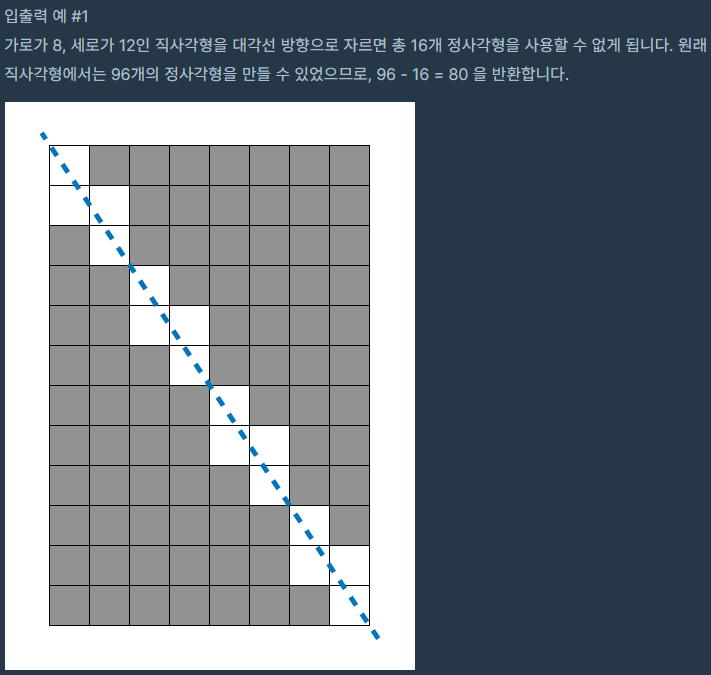
특별한 연산이나 함수의 사용보다는 어떠한 규칙성이 있을 것 같다는 생각이 들어서 그림을 그려가며 접근하려고 했다. 따라서 주어진 입출력외의 또 다른 테스트케이스를 만들어서 그림을 그려보았다.

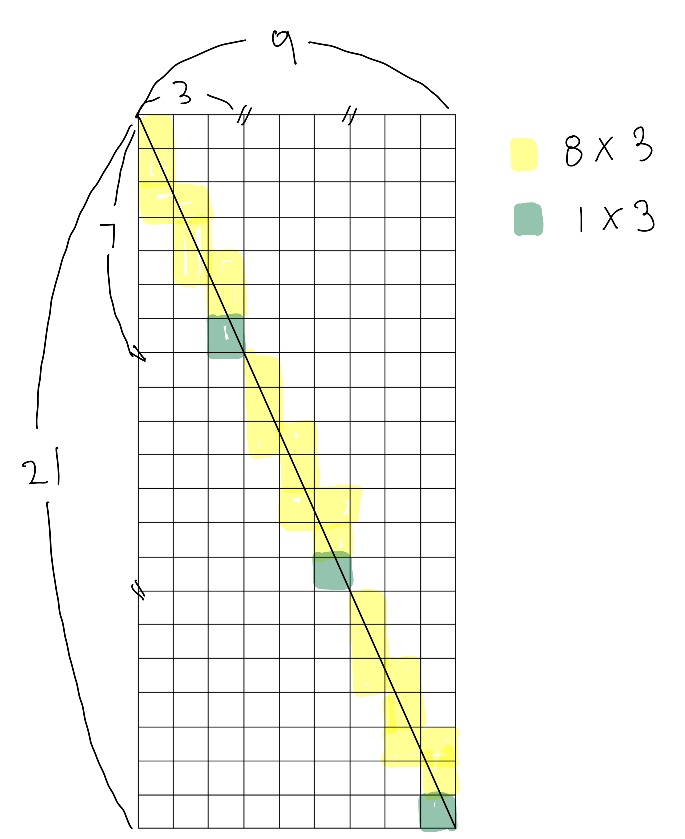
어떠한 사각형의 꼭지점을 지나는 점을 기점으로 규칙적인 모양이 반복되고 있었고 그 집합의 크기역시 동일하게 반복되고 있었다. 그림을 보면 세로를 7, 가로를 3으로 나누면 같은 개수의 사각형이 사용 불가능인 것이다. 이때 사각형의 같은 모양이 세번이 반복되는것이나 다름이 없는데 이는 가로,세로의 최대공약수에 해당했다. 즉 문제는 사각형의 개수를 구하는 규칙이었다.

입출력 예시1번에서는 가로가 2, 세로가 3인 크기안에서 4개의 사각형이 사용 불가능했고,
내가 그린 그림에서는 가로가 3, 세로가 7인 크기안에서 9개의 사각형이 사용 불가능했다.
즉 가로+세로-1이 사용이 불가능한 사각형의 개수인것을 알 수 있다.

정리해보자면

1. 주어진 w,h의 최대공약수를 구한다.
2. 최대공약수로 각각의 w,h를 나눴을때 나오는 작은 단위의 가로, 세로의 길이를 구한다.
3. 그때의 가로,세로 즉, GCDw+GCDh-1에 최대공약수를 곱해서 answer에 더한다.

레고레고

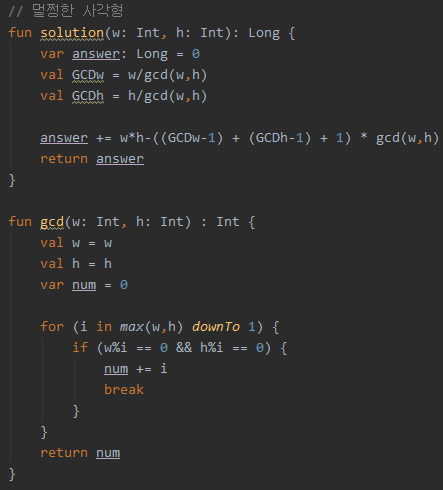
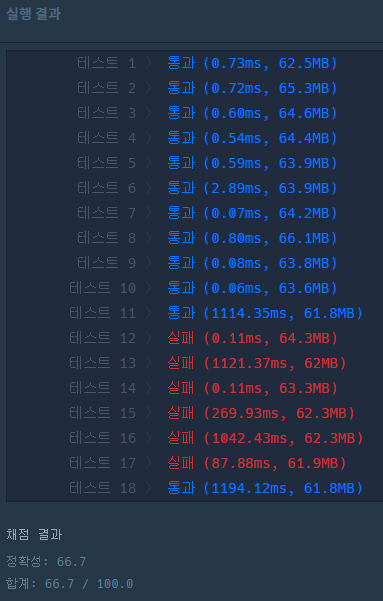
문제의 제한사항을 보면

이러한 항목이 있다. 아마 Int형으로 계산하면 범위가 넘어가는 경우가 발생하는 것 같아서 w,h를 곱하는 과정에서 타입을Long으로 바꿔주었다.

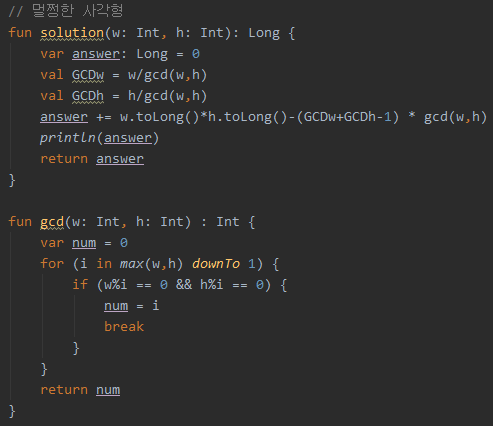
통과~~!!