import sys
def max_square(l, r):
if l == r:
return h[l]
else:
m = (l + r) // 2
nl = m
nr = m + 1
nh = min(h[nl], h[nr])
tmp = nh * 2
cnt = 2
while True:
if (h[nl] == 0 or nl == l) and (h[nr] == 0 or nr == r):
break
elif h[nl] == 0 or nl == l:
if h[nr + 1] < nh:
nh = h[nr + 1]
nr += 1
elif h[nr] == 0 or nr == r:
if h[nl - 1] < nh:
nh = h[nl - 1]
nl -= 1
else:
if h[nl - 1] > h[nr + 1]:
if h[nl - 1] < nh:
nh = h[nl - 1]
nl -= 1
else:
if h[nr + 1] < nh:
nh = h[nr + 1]
nr += 1
cnt += 1
tmp = max(tmp, nh * cnt)
return(max(max_square(l, m), max_square(m + 1, r), tmp))
while True:
h = list(map(int, sys.stdin.readline().split()))
if h[0] == 0:
break
print(max_square(1, len(h) - 1))
분할 정복이 무엇인지 조금은 알게 된 문제였다.
분할정복의 개념을 찾아보면 분할정복은 3단계로 나뉜다고 한다.
분할: 문제를 동일한 유형의 여러 하위 문제로 나눈다.
정복: 가장 작은 단위의 하위 문제를 해결하여 정복한다.
조합: 하위 문제에 대한 결과를 원래 문제에 대한 결과로 조합한다.
이를 사용해 문제를 풀어보도록 하자.
풀이
우리가 해야할 것은 나눴던 조각을 합치면서 각각의 최댓값과 두개를 합쳤을 때 만들어지는(경계선에 걸쳐있는) 최댓값 총 3개의 값을 비교해 합쳐진 조각의 최댓값을 얻는 것이다.
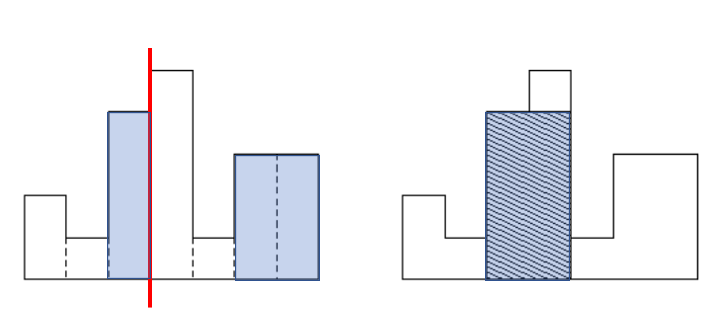
위 그림을 두 조각을 합칠 때 보면 왜 경계선에서 만들어지는 최댓값을 고려해야하는지 알 수 있다.
1) 히스토그램을 너비가 1이 될 때까지 반으로 분할한다. 분할한 조각의 너비가 1이 되면 그 직사각형의 최댓값인 그 직사각형의 높이를 반환한다.
if l == r:
return h[l]
2) 이제 조각들을 붙이는 과정이다. 너비가 1이 아니라면(l != r) 반으로 나눴을 때 각각의 조각들의 최댓값과 경계선에 걸쳐있는 최댓값 중 최댓값을 반환한다.
return(max(max_square(l, m), max_square(m + 1, r), tmp))
이제 경계선에 걸친 최댓값인 tmp를 구해보자.
2 - 1) 먼저 경계선에 걸쳐있는 최댓값이므로
nl = m = (l + r) // 2, nr = m + 1 두 점에서 시작한다.
nl 또는 nr 그 높이가 최댓값이라면 이미 너비를 최소인 1으로 분할했을 때 구한 최댓값이므로 고려할 필요가 없기 때문이다.
그리고 이 너비가 2인 직사각형의 높이는 당연히 nl, nr 중 작은 값(높이가 낮은 것)이다.
nh = min(h[nl], h[nr])
cnt = 2 (너비)
tmp = nh * cnt (경계선에 걸친 직사각형의 넓이)
2 - 2) 이제 nl, nr을 한 칸씩 좌, 우로 늘려가며 생기는 직사각형의 넓이를 구한다.
이때 nl 또는 nr이 양 끝 인덱스인 l, r과 같아지거나 높이가 0인 직사각형을 만나면 탐색을 멈춘다.
if (h[nl] == 0 or nl == l) and (h[nr] == 0 or nr == r):
break
만약 한쪽이 끝 인덱스를 만나거나 0을 만났다면 반대쪽만 한 칸씩 늘려준다.
2 - 3) 양쪽 다 늘려갈 수 있을 때에는 그 다음 한 칸씩의 높이를 비교해 더 높은 쪽을 먼저 늘린다. 우리는 넓이의 최댓값을 구해야 하기 때문이다.
if h[nl - 1] > h[nr + 1]:
if h[nl - 1] < nh:
nh = h[nl - 1]
nl -= 1
else:
if h[nr + 1] < nh:
nh = h[nr + 1]
nr += 1
이때 현재 높이(nh)와 nl - 1 또는 nr + 1의 높이 중 더 낮은 값을 nh로 재설정한다.
2 - 4) 한 칸씩 이동할 때마다 너비(cnt)를 1씩 늘려주고 그때마다의 직사각형의 넓이(nh * cnt)와 tmp를 비교해 그 중 최댓값을 tmp로 갱신해준다.
하루종일 고민하다 푼 문제여서 코드가 조금 더럽긴 해도 풀었다는 점에 뿌듯함을 느낀다.
스택을 이용한 풀이가 있던데 한 번 찾아봐야겠다.
피드백 환영합니다
-끝-
