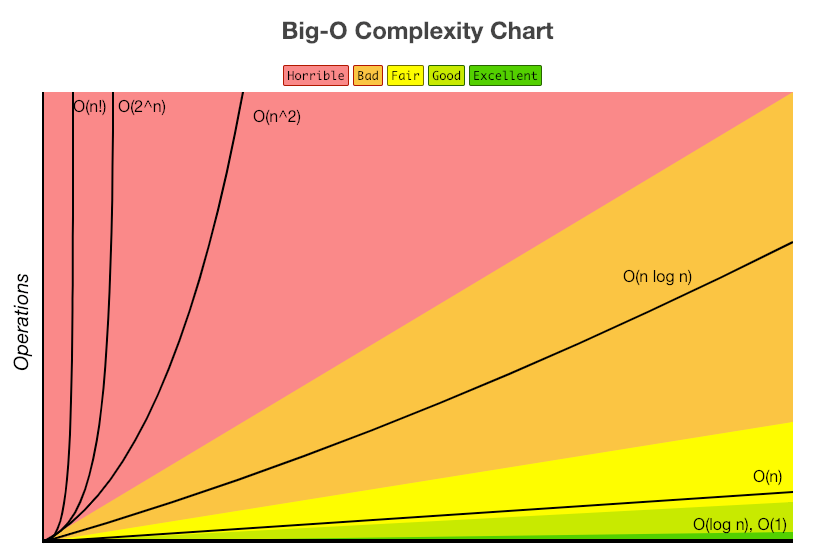
시간복잡도가 뭐야?
- 알고리즘을 설계할 때, 가장 중요한것은 바로 시간이다. 어떠한 문제가 닥쳤을 때, 최소한의 시간으로 문제를 풀면 시간상의 이득이 있기 때문이다. 이렇게 최소한의 시간으로 문제를 푸는 알고리즘을 좋은 알고리즘이라고 하는데, 이때 걸리는 시간을 수학적인 표현으로 나타내 알아보기 쉽도록 한것이 시간복잡도이다.
어떠한것들이 있나?
- Big-O(빅-오)
- 최악의 경우를 고려함. 즉 최악의 경우 시간이 어느정도까지 걸릴 수 있다를 나타냄.
- 가장 많이 사용함. - Big-Ω(빅-오메가)
- 최선의 경우를 고려함. 즉 최선의 경우 시간이 어느정도까지 걸릴 수 있다를 나타냄. - Big-θ(빅-세타)
- 중간(평균)의 경우를 고려함. 즉 몇번 실행했을때 시간이 평균 어느정도까지 걸릴 수 있다를 나타냄.
Big-O(빅-오)?
-
O(1)
- Constant Complexity 라고 하며, 입력값이 증가하더라도 시간이 늘어나지 않는다. 즉 입력값의 크기와 관계없이 즉시 출력값을 얻어낼 수 있다는 의미이다.
- 예시는 아래와 같다.function O1_algorithm(arr, index) { return arr[index]; } let arr = [1, 2, 3, 4, 5]; let index = 1; let result = O_1_algorithm(arr, index); console.log(result); // 2- 위 예시를 보면 함수의 인자로 전달되는 입력값이 아무리 커져도 즉시 출력값을 얻어낼 수 있다는걸 알 수 있다. 즉 예를 들어 arr의 길이가 100만이라 하더라도 즉시 해당 index에 접근해 값을 반환할 수 있다는 말이다.
-
O(n)
- Linear Complexity 라고 하며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미한다. 즉 입력값이 1일때 1초의 시간이 걸리고, 입력값을 100으로 증가시켰을땐 100초의 시간이 걸린다는 의미이다. 위와 같은 알고리즘을 구현했다면 해당 알고리즘은 O(n)의 시간 복잡도를 가진다고 할 수 있다.
- 예시는 아래와 같다.function On_algorithm(n) { for(let i = 0; i < n; i++) { // do something for 1 second } }- 위 예시를 보면 함수의 입력값 n이 1 증가할 때마다 코드의 실행 시간이 1초씩 증가하게 된다. 즉 입력값이 증가함에 따라 같은 비율로 걸리는 시간이 늘어나게 될때에 이러한 함수는 O(n)의 시간 복잡도를 가진다고 볼 수 있다.
- 만약 위 함수에서 do something for 1 second이 아니고 do something for 2 seconds 이나 do something for 5 seconds 라 하더라도 시간이 늘어났기때문에 시간복잡도가 O(2n) 이나 O(5n) 아니야? 라고 생각할 수 있겠지만, 그렇지 않다.
- 중요한것은 증가하는 입력값과 같은 비율로 시간이 증가하는가?를 고려하는것이기 때문에 do something for 2 seconds 이나 do something for 5 seconds 라 하더라도 입력값과 같은 비율로 시간이 증가하게 된다면 해당 함수는 O(n)의 시간 복잡도를 가졌다고 볼 수 있다.
-
O(log n)
- Logarithmic Complexity 라고 하며, Big-O표기법중 O(1) 다음으로 빠른 시간 복잡도를 가진다. 해당 시간 복잡도를 가장 이해하기 쉽게 설명하자면 Up & Down 게임을 예시로 들면 이해하기가 조금 편하다. 1부터 50까지 숫자 중 랜덤으로 아무 숫자나 하나를 정해서 상대방이 해당 숫자를 맞추는 게임인데, 상대방이 말하는 숫자를 듣고 랜덤으로 정한 하나의 숫자가 어디에 있는지 Up인지 Down인지 알려주고 그런식으로 쭉 계속 해나가면서 처음 랜덤으로 정한 숫자를 맞추는 게임이다. 이 게임의 특징은 한번 숫자를 말할때마다 숫자가 Up인지 Down인지 맞출 수 있는 경우의 수가 반으로 줄어든다는것인데 O(log n)의 시간 복잡도를 가진 알고리즘도 이와 같다.
-
O(n2)
- Quadratic Complexity 라고 하며, 입력값이 증가함에 따라 시간이 입력값의 제곱수 비율로 증가하는 것을 의미한다. 즉 입력값이 1일때 1초의 시간이 걸리던 알고리즘에 입력값을 5로 줬더니 25(5x5)초의 시간이 걸렸다 라고 한다면 해당 알고리즘은 O(n2)의 시간 복잡도를 가진 알고리즘이라고 할 수 있겠다.
- 예시는 아래와 같다.function O_quadratic_algorithm(n) { for (let i = 0; i < n; i++) { for (let j = 0; j < n; j++) { // do something for 1 second } } } function another_O_quadratic_algorithm(n) { for (let i = 0; i < n; i++) { for (let j = 0; j < n; j++) { for (let k = 0; k < n; k++) { // do something for 1 second } } } } -
O(2n)
- Exponential Complexity 라고 하며, Big-O 표기법 중 가장 느린 시간 복잡도를 가진다. 종이를 42번 접으면 그 두께가 지구에서 달까지의 거리보다 커진다는 이야기가 있는데 그 이유는 고작 종이처럼 얇은 것일지라도 한번 접을때마다 그 두께가 2배로 늘어나기 때문이다. 즉 입력값이 +1로 증가할때마다 따라 걸리는 시간이 두배로 늘어나는 알고리즘이 있을때 이러한 알고리즘을 O(2n)의 시간 복잡도를 가진 알고리즘이라고 한다.
- 예시는 아래와 같다.function fibonacci(n) { if (n <= 1) { return 1; } return fibonacci(n - 1) + fibonacci(n - 2); }- 재귀로 구현한 피보나치 수열은 O(2n)의 시간 복잡도를 가진 대표적인 알고리즘으로, 만약 n값을 100 이상으로 한다면 평생 결과를 반환받지 못할 수 도 있다.
