프로그래머스 - 정수 삼각형

https://programmers.co.kr/learn/courses/30/lessons/43105

동적 계획법으로 풀 수 있는 문제이다.

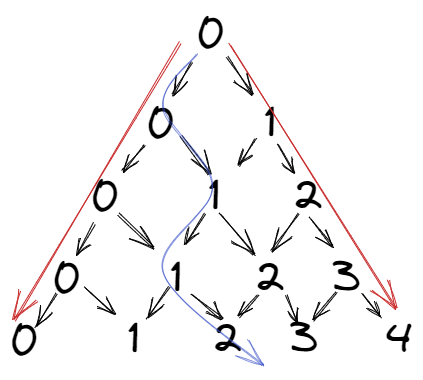
만약 그리디 알고리즘을 선택했다고 하면, 다른 경로에서 최댓값이 나오는 경우가 있을 수 있다. 갈 수 있는 경로의 최댓값을 골라도, 그 전체 합보다 큰 값이 다른 경로에 어느 한 곳에 있을 수 있기 때문이다.

그리고 삼각형의 높이를 n이라고 했을 때, 한 점까지의 경로의 최댓값은 삼각형 높이가 n - 1일 때의 합을 포함하므로, 동적 계획법을 이용하여 높이가 1일 때부터 시작하여 각 지점까지 가는 경로의 최댓값을 구한다.

위의 그림은 각 숫자를 index로 표현한 것이다. 여기서 왼쪽 변과 오른쪽 변의 제일 끝까지 가는 경로는 오직 하나 (0->0->...과 0 -> 1 -> 2 -> ...)이므로 단순히 계산할 수 있다.

그 외의 경우는 index를 j라고 하면, 그 윗 변의 j - 1과 j 중에서 최댓값을 고른다.

class Solution {
    public int solution(int[][] triangle) {
        for (int i = 1; i < triangle.length; i++) {
            int[] row = triangle[i];
            int[] prevRow = triangle[i - 1];
            
            // 양쪽 끝의 길은 하나만 존재
            row[0] += prevRow[0];
            row[row.length - 1] += prevRow[prevRow.length - 1];
            
            // 그 외의 경우, 삼각형 윗변에서 [j]나 [j - 1]중 큰 값을 선택한다.
            for (int j = 1; j < row.length - 1; j++) {
                row[j] += Math.max(prevRow[j], prevRow[j - 1]);
            }
        }
        
        int answer = 0;
        
        for (int sum : triangle[triangle.length - 1]) {
            if (answer < sum) {
                answer = sum;
            }
        }
        
        return answer;
    }
}