노션에 B-Tree에 대해 정리해놨던 글을 옮겼습니다! 그림 배경이 투명으로 되었네요.. 다크모드를 해제하고 봐주세요 ㅜㅜ

B-Tree란?

탐색 성능을 높이기 위해 고안된 트리의 한 종류로, 모든 leaf node가 같은 depth를 가지는게 특징인 균형잡힌(Balanced) 트리입니다.

인덱스를 구성할 수 있는 자료구조는 Hash Table과 B+Tree가 있는데 그 중 B+Tree의 근간?이 되는 Tree입니다.

먼저 Hash Table은 높은 검색 성능을 자랑하지만 DB의 특성상 부등호 연산으로 검색을 하는 경우가 많아 정렬이 되지 않는 Hash Table을 사용하기에는 무리가있기 때문에 B+Tree를 사용합니다.

그래서 먼저 B+Tree의 근간인 B-Tree를 알아봅니다.

일반적인 트리일 경우 한쪽으로 편향된 트리가 만들어질 경우 탐색 성능이 O(logN)에서 O(N)으로 저하될 가능성이 있어 균형이 잡혀있어야합니다.

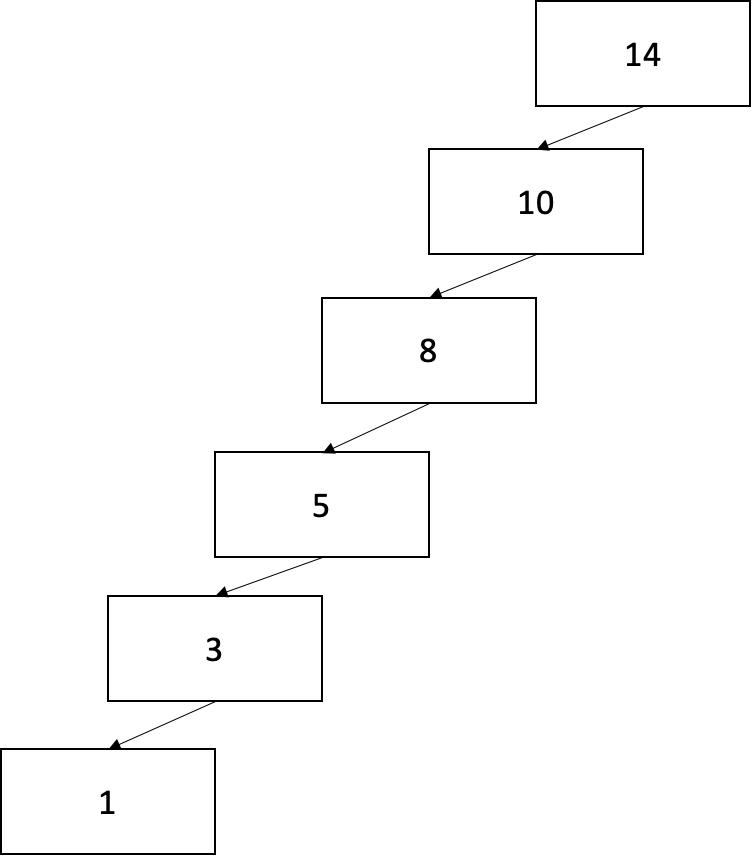
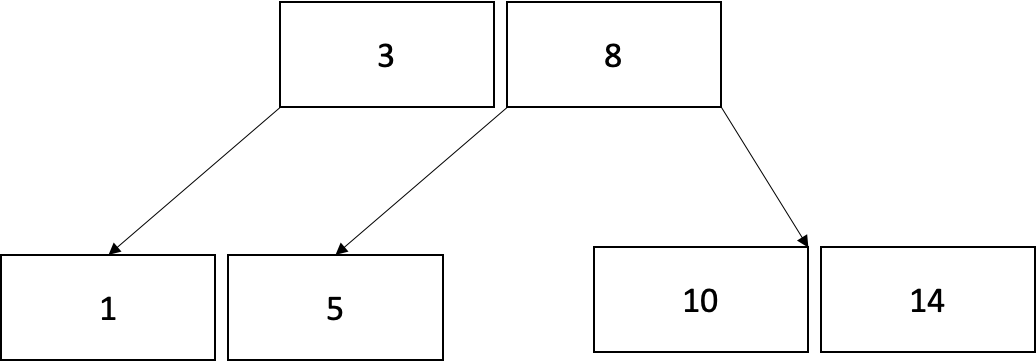
왼쪽 트리는 1을 찾기위해 6번을 순회해야하지만 오른쪽 트리는 균형이 잡혀있어 2번만 순회하면 됩니다.

또한, 이진 트리와 다르게 하나의 노드에 많은 key 값을 가질 수 있습니다. 하나의 노드에 M개의 key값이 들어간다면 M차 B-Tree라고 부릅니다.

B-Tree의 특징

• 각 노드의 데이터들은 정렬되어있습니다.
• 중복되지 않습니다.
• 모든 leaf node는 같은 level에 위치합니다.
• Root node는 항상 2개 이상의 자식 node를 갖습니다. 단, Root가 Leaf일 경우는 제외입니다.
• M차 B-Tree일 경우, Root node와 Leaf node를 제외한 모든 node는 최소 M/2, 최대 M개의 서브트리를 갖습니다.

B-Tree 단점

• 삽입, 수정, 삭제에 따라 트리의 균형을 맞추는 작업이 필요해 성능에 문제가 발생할 수 있습니다.

B-Tree의 삽입

1. 트리가 비어있다면 루트 노드를 할당하고 k를 삽입
2. 트리가 비어있지 않다면 삽입할 적절한 리프노드를 탐색 후 삽입
3. 리프노드가 가득찼다면 분할
4. 분할 시 중간 값 데이터를 부모노드로 보냄

예시로 아래 트리 상태에서 15를 삽입하는 과정을 살펴보겠습니다.

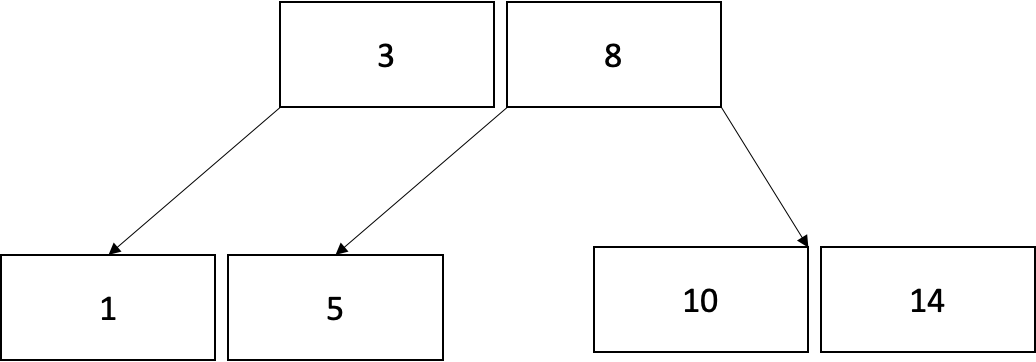
1) 15를 삽입할 적절한 위치를 찾았지만 리프노드가 가득차서 분할이 필요합니다.

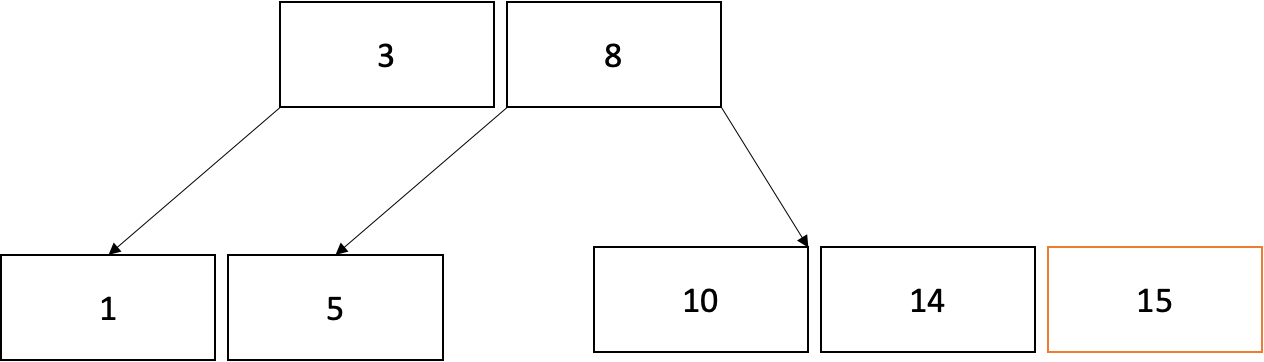
2) 10, 14, 15 중 중간값인 14를 부모노드로 보냅니다.

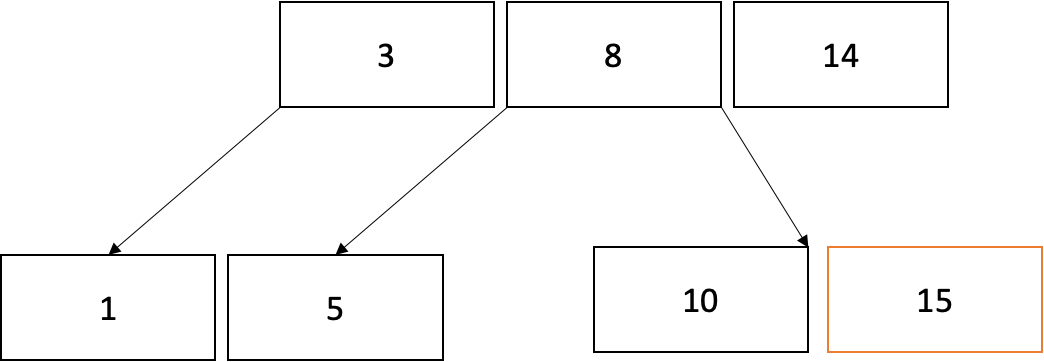
3) 부모노드인 루트노드도 가득 찼으므로 3, 8, 14중 중간값인 8을 새로운 루트노드로 만듭니다. (삽입 완료)

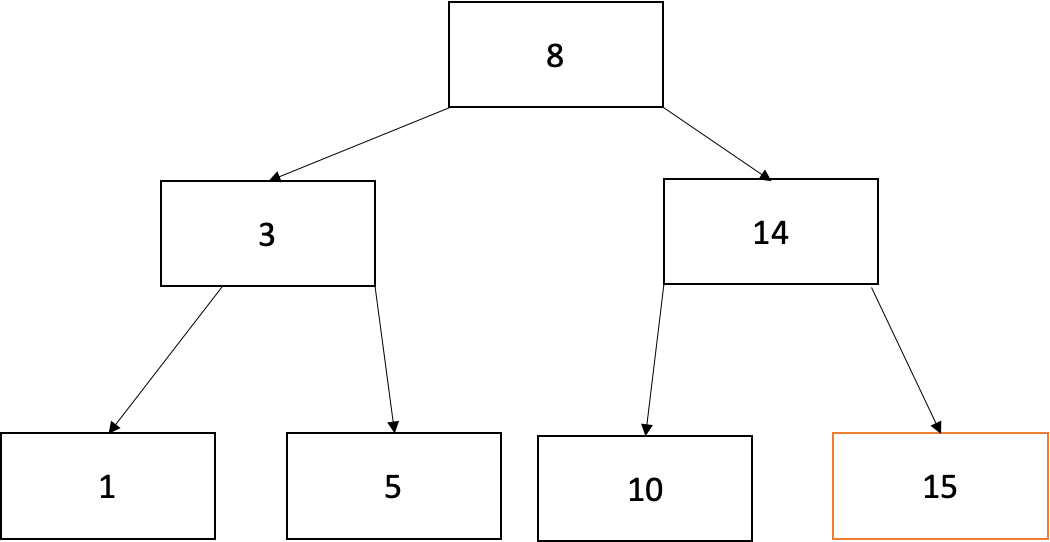
B-Tree의 삭제

삭제는 삭제의 대상이 어떤 상태인지에 따라 다릅니다.

1. 삭제의 대상이 Leaf Node에 속해있을 때
   a. 현재 node의 key 수가 최소보다 큰 경우 
   b. 현재 node의 key 수가 최소이고, 왼쪽 또는 오른쪽 형제 node의 key 수가 최소보다 큰 경우 
   c. 현재 node와 왼쪽, 오른쪽 형제 node의 key 수가 최소이고, 부모 node의 key 수가 최소보다 큰 경우 
   d. 현재 node와 왼쪽, 오른쪽 형제 node, 부모 node 모두 key 수가 최소인 경우
2. 삭제의 대상이 Leaf Node에 속해있지 않을 때
   a. 현재 node 또는 자식 node의 key 수가 최소보다 큰 경우
   b. 현재 node와 자식 node 모두 key 수가 최소인 경우

삭제의 대상이 Leaf Node에 속해있을 때

a. 현재 node의 key 수가 최소보다 큰 경우

아래 트리에서 15를 삭제하고 싶다면 트리의 형태를 유지하는데 문제 없으므로 그냥 삭제하면 됩니다.

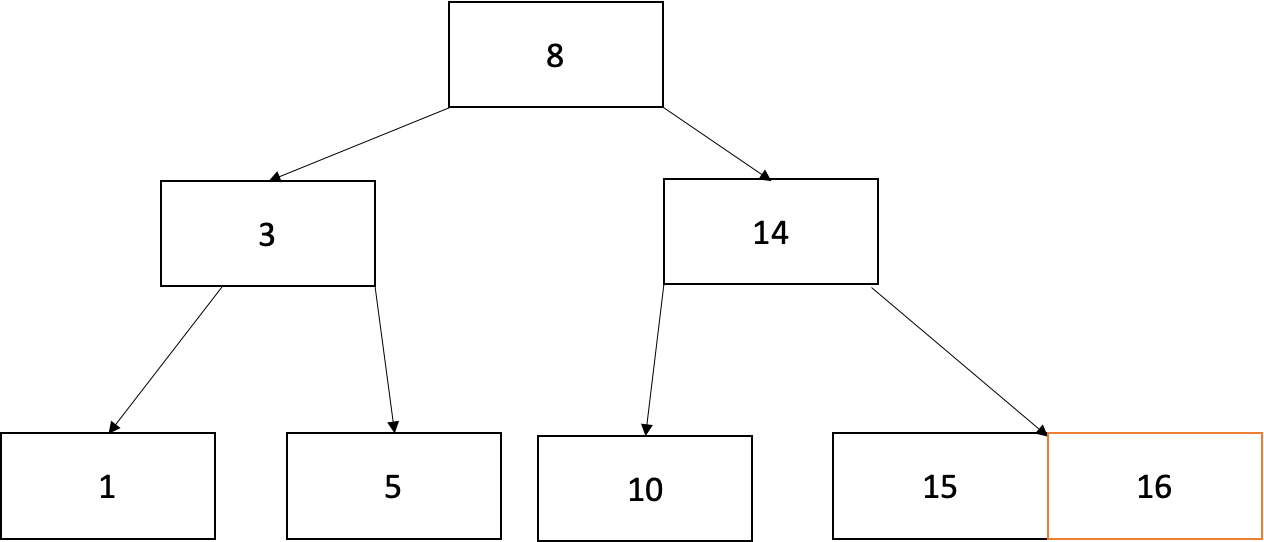
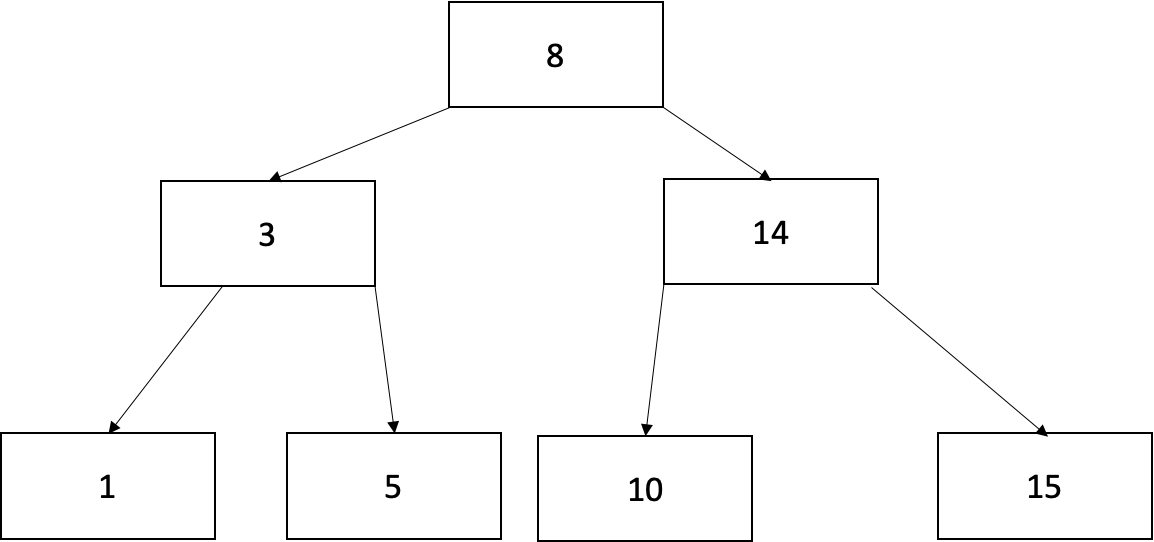
b. 현재 node의 key 수가 최소이고, 왼쪽 또는 오른쪽 형제 node의 key 수가 최소보다 큰 경우 

쉽게 말해서 현재 node를 삭제하면 트리의 형태가 망가지고 형제 노드에서 값을 빌려올 수 있는 경우를 말합니다.

아래와 같은 트리 형태에서는 10을 삭제하고자 했을 때 이미 key 수가 최소입니다. 대신 오른쪽 형제 노드에게서 값을 가져올 수 있는데 오른쪽 형제노드의 min값을 가져오면 됩니다. (왼쪽 형제노드에게서 가져올 경우 max 값을 가져옵니다. 둘다 빌려올 수 있을 경우 아무거나 하나 선택)

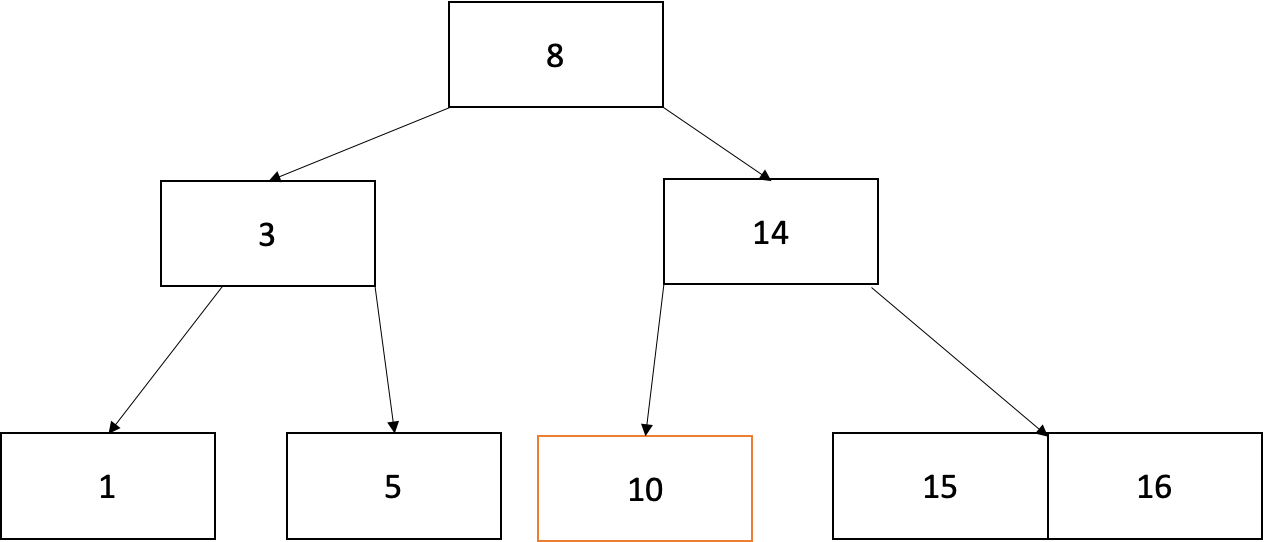
먼저 10은 부모노드인 14로 대체합니다.

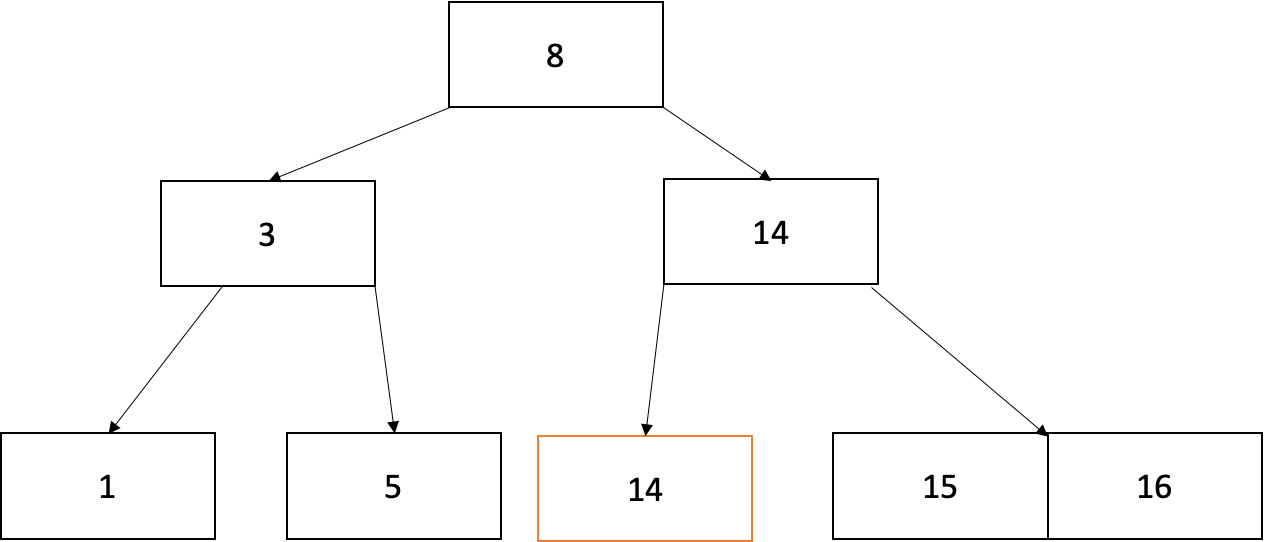
그리고 부모노드를 오른쪽 형제노드의 min값인 15와 바꿔줍니다.

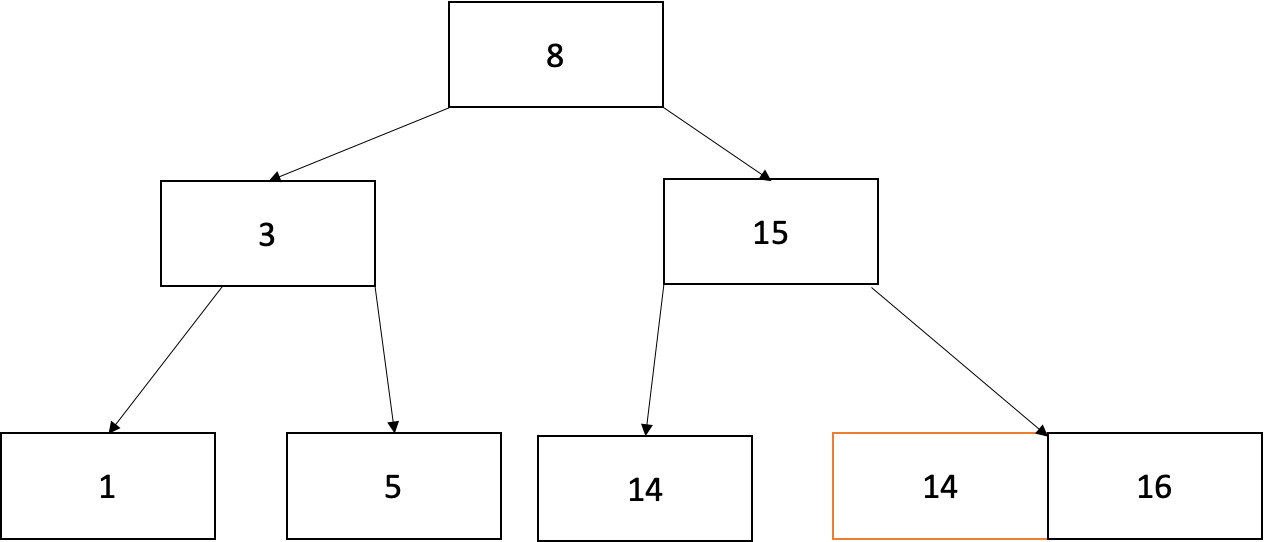
바꿔서 리프노드로 가게된 14를 삭제해줍니다.

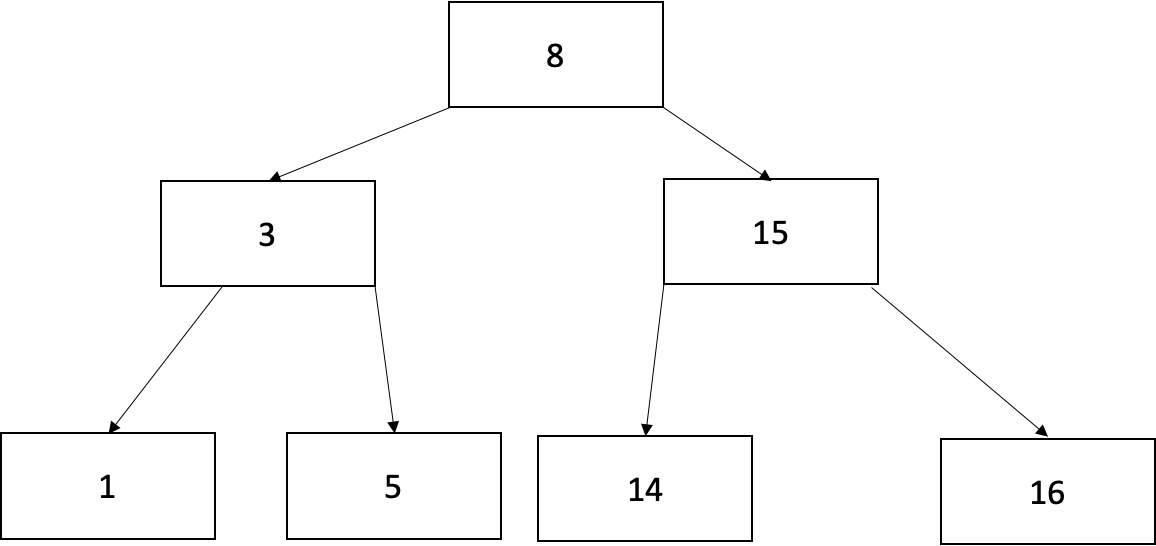
c. 현재 node와 왼쪽, 오른쪽 형제 node의 key 수가 최소이고, 부모 node의 key 수가 최소보다 큰 경우 

다시 말해서 방금 처럼 왼쪽, 오른쪽에서 빌려올 수는 없고 부모 노드에서 가져올 수 있는 경우를 말합니다.

아래와 같은 트리에서 4를 삭제하고자 할 때, 부모노드인 (3,5)의 자식 노드 수가 3개여야 하지만 2개가 되어버려 최소 유지 개수를 만족하지 못하고. 왼쪽 오른쪽 모두 노드 내 key값이 한개라서 가져올 수 없습니다.

대신 부모노드를 분할해서 사용할 수 있습니다.

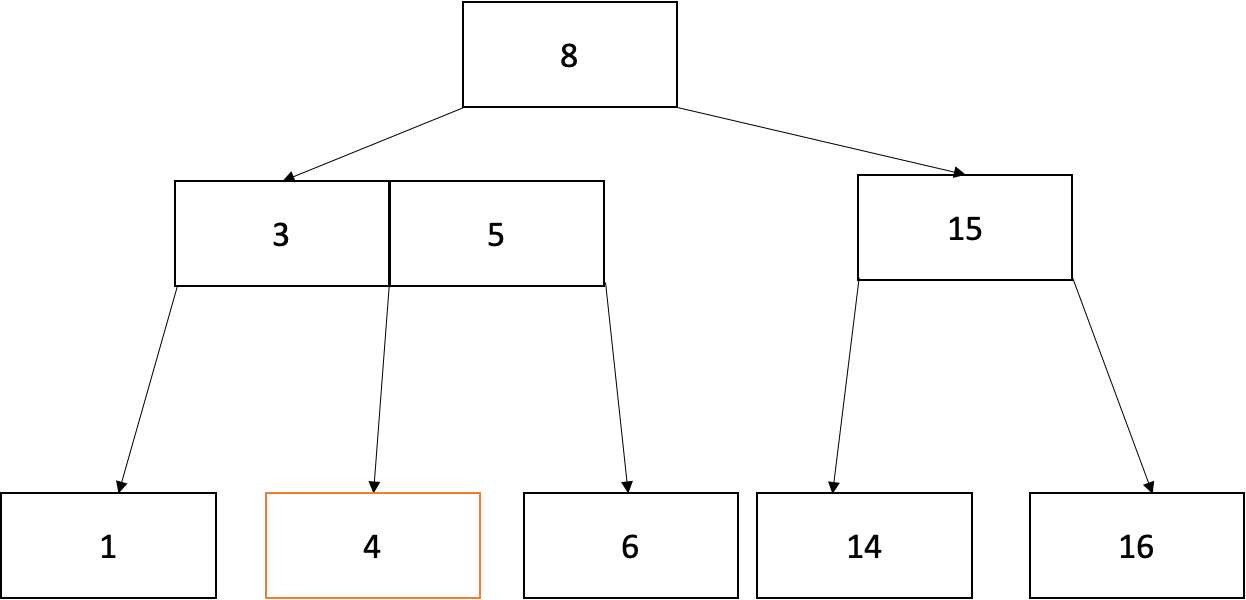
부모노드의 key 중 3을 분할해서 자식노드와 합쳐줍니다. (제거 완료)

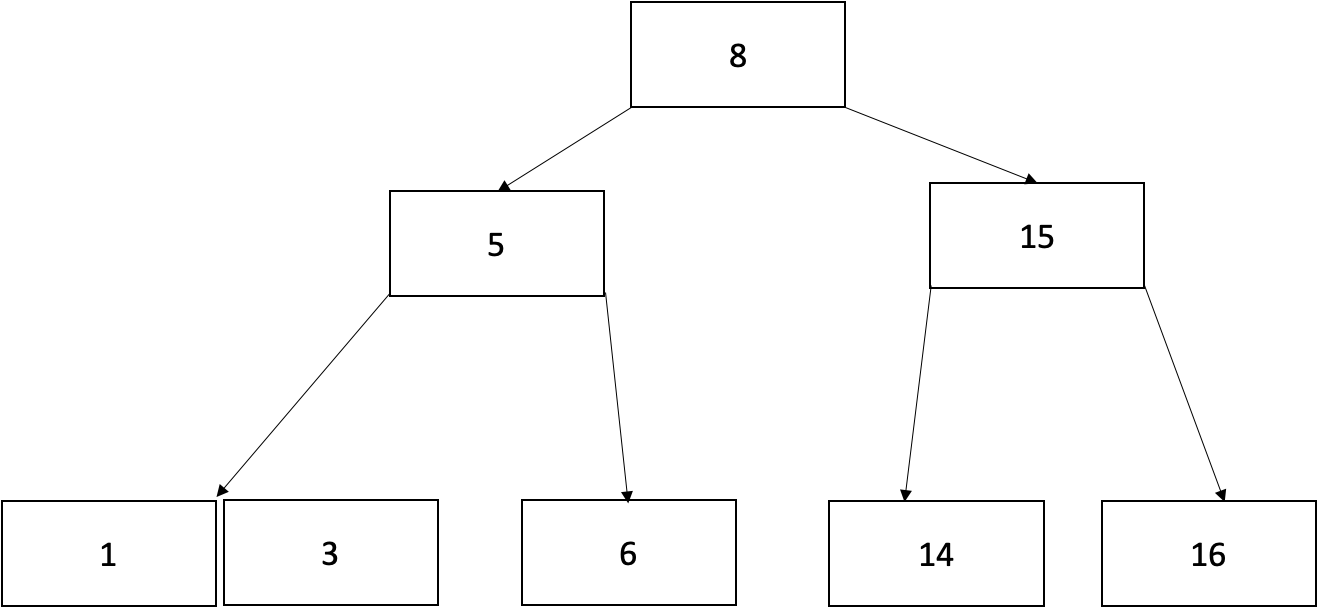
d. 현재 node와 왼쪽, 오른쪽 형제 node, 부모 node 모두 key 수가 최소인 경우

case 2-b와 같습니다. 뒤의 설명을 참고합시다.

삭제의 대상이 Leaf Node에 속해있지 않을 때

a. 현재 node 또는 자식 node의 key 수가 최소보다 큰 경우

아래 트리에서 8을 삭제하고자 했을 때의 상황입니다.

8을 삭제할 때 8의 자리를 대체해줄 자식노드를 찾아 대체 해줍니다. 그 대상은 왼쪽 자식 노드의 키값 중 최대값, 또는 오른쪽 자신 노드의 키값 중 최소 값입니다.

왼쪽 자식노드의 key값 중 최대값인 6과 대체할때의 과정을 살펴보겠습니다.

8과 6을 바꿔줍니다. 그리고 leaf node에 속해있는 key 값의 삭제 방법과 같습니다.

이 경우에는 b.현재 node의 key 수가 최소이고, 왼쪽 또는 오른쪽 형제 node의 key 수가 최소보다 큰 경우와 같습니다

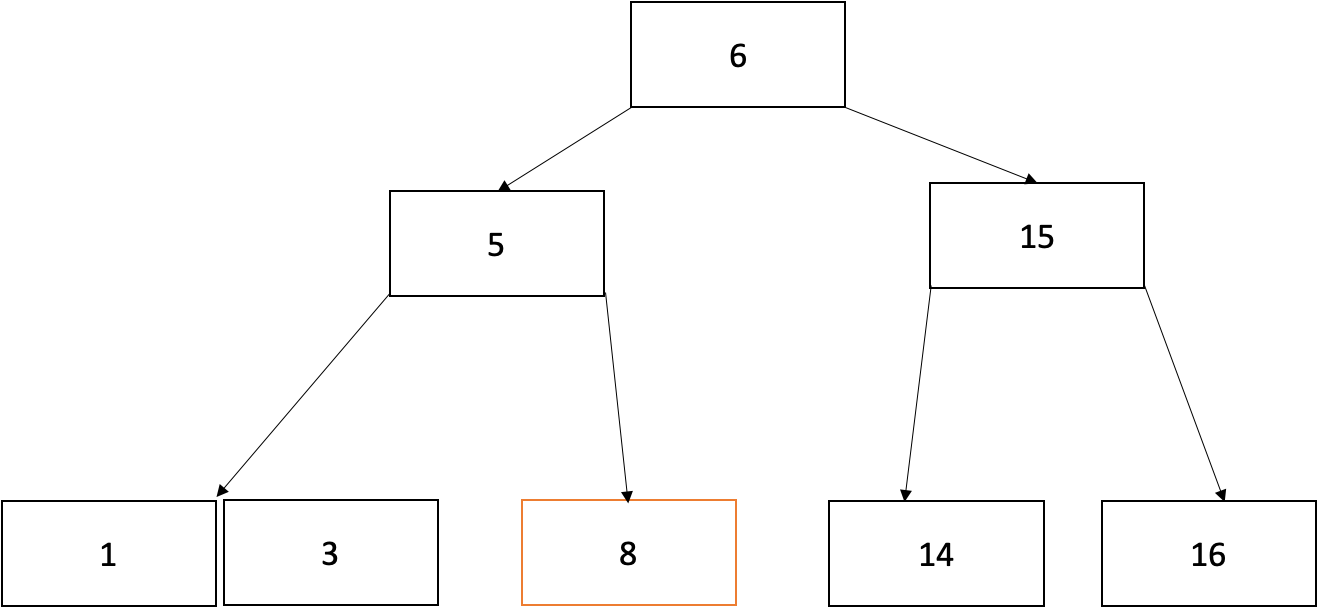
8을 부모노드의 key값인 5로 바꿔주고 부모노드의 값을 왼쪽 형제노드의 key값 중 최대인 3으로 변경해줍니다. (삭제 완료)

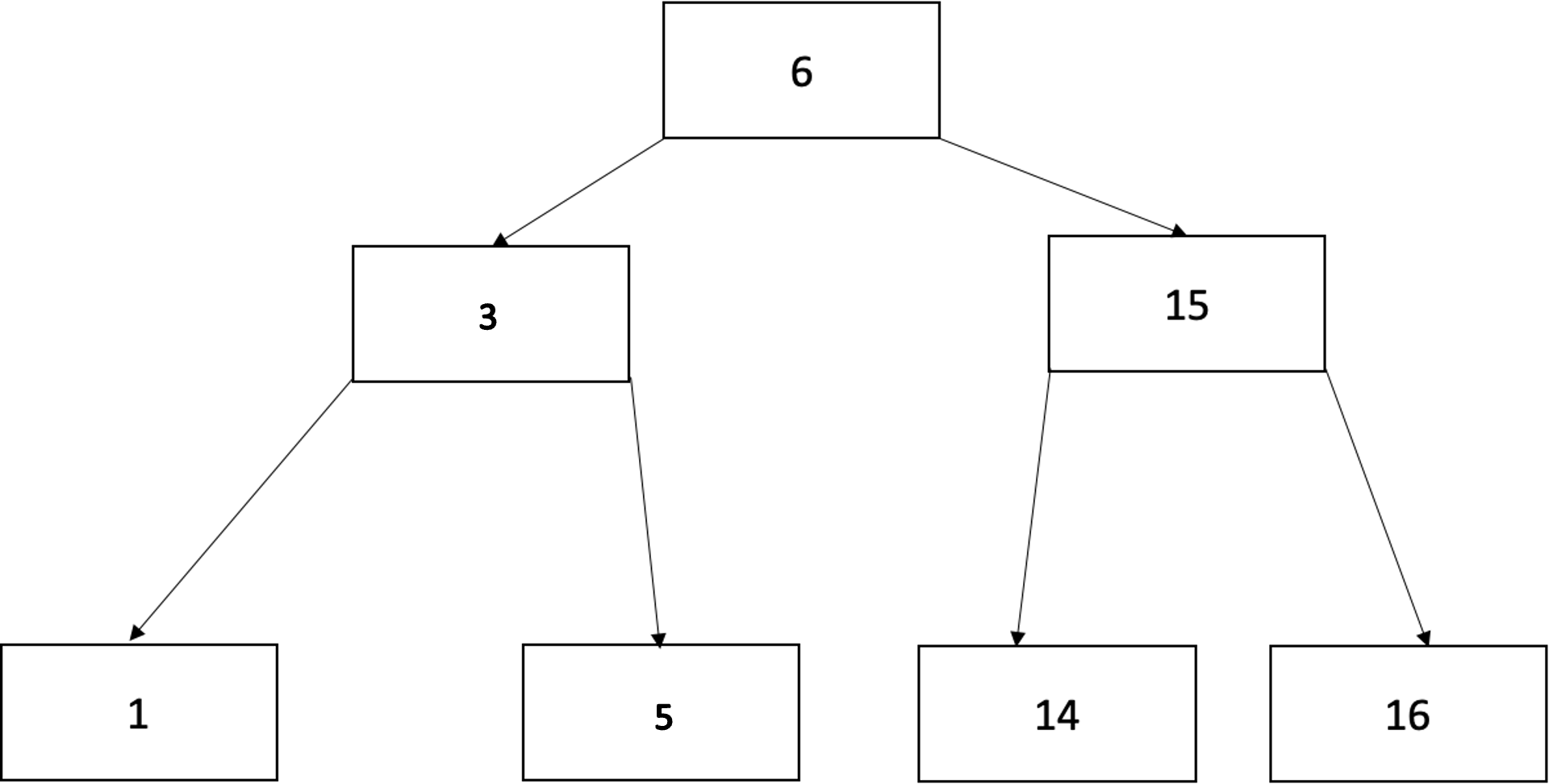
b. 현재 node와 자식 node 모두 key 수가 최소인 경우

트리의 재구조화가 필요합니다.

삭제할 값을 K라고 했을 때,

1. K를 삭제하고 K의 자식을 하나로 합친다. 이 합친 노드를 N1이라고 한다.

2. K의 부모노드를 K 형제노드에 합친다. 이 합친 노드를 N2라고 한다.

3. N1을 N2의 자식이 되도록 연결한다.

   4-a. 만약 N2의 key 수가 최대보다 크면 key 삽입 과정과 동일하게 분할한다.

   4-b. N2의 key 수가 최소보다 작다면 2번 과정으로 돌아가 반복한다.

8을 삭제 시 트리의 형태를 유지할 수 없습니다. 트리 재구조화가 필요합니다.

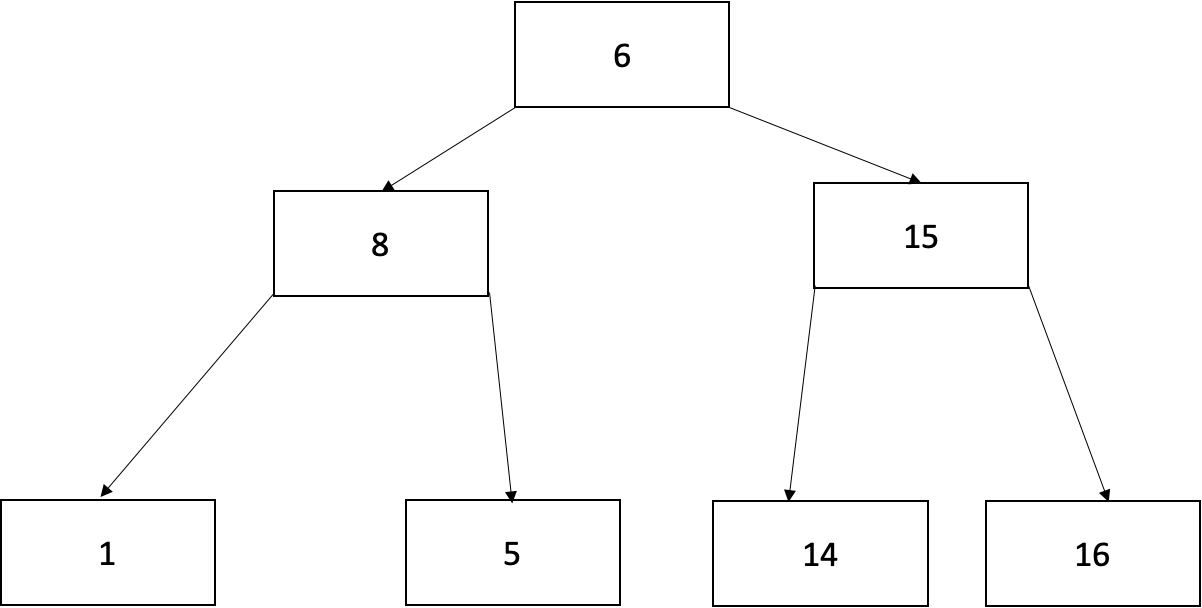
8을 삭제하고 8의 자식노드인 1,5를 하나의 노드로 합쳐줍니다. (N1)

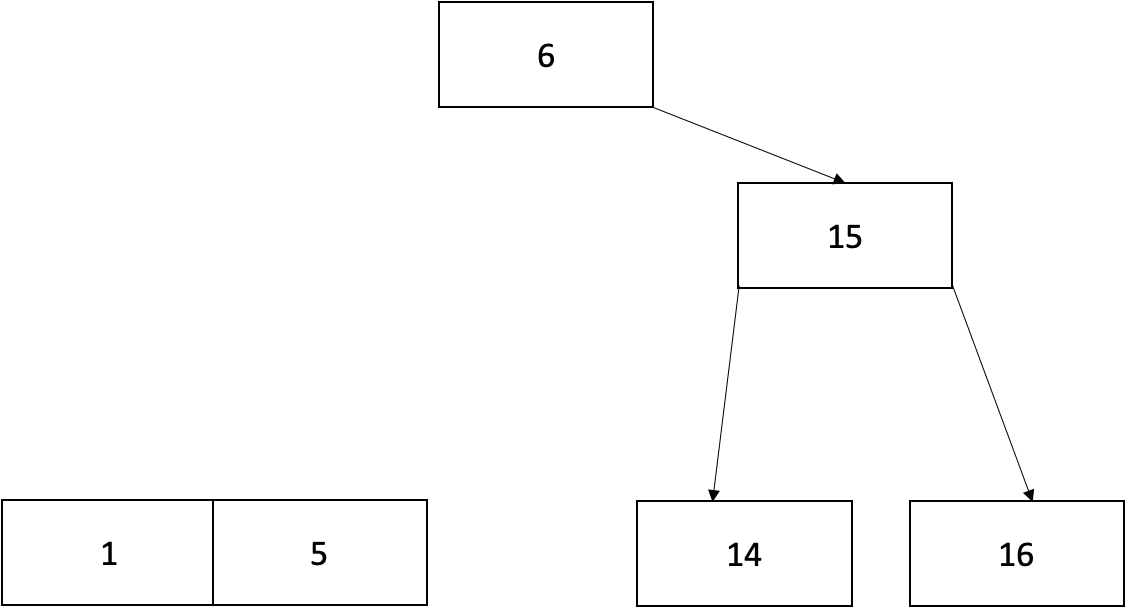
삭제한 8의 부모노드인 6을 8의 형제노드인 15와 합쳐줍니다. (N2)

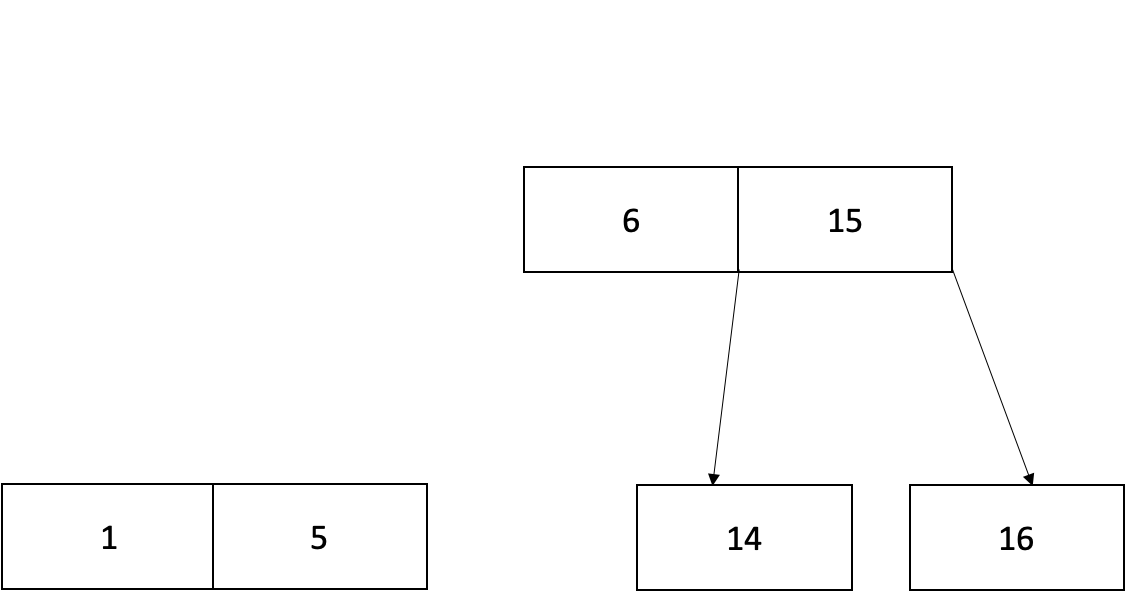
N1을 N2의 자식이 되도록 연결해줍니다.

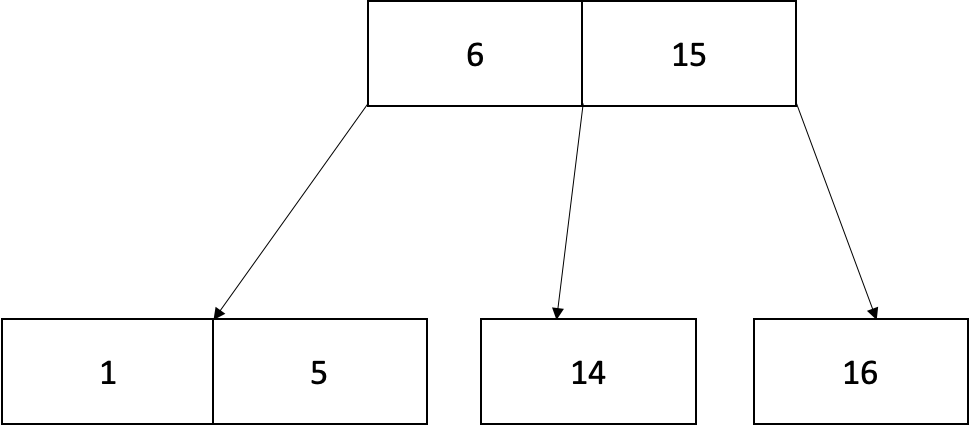
현재 예시에서는 4번 과정이 필요가 없지만 앞서 설명한 케이스들로 해결해나가면 됩니다.

B+Tree

B-Tree의 확장 개념으로 B-Tree는 모든 node에 key와 data를 담을 수 있지만, B+Tree는 오직 leaf노드에만 data를 저장합니다. 그리고 이 Leaf node끼리는 linked list로 연결되어 있습니다.

Leaft Node에 데이터를 저장하기 때문에 올바르게 데이터를 찾아가기 위해 B-Tree와는 다르게 key가 중복될 수 있습니다.

B+Tree 장점

• 하나의 노드에 더 많은 key들을 담을 수 있기 때문에 트리의 높이가 낮아진다.
• 풀 스캔 시, B+Tree는 리프 노드에 데이터가 모두 있기 때문에 한번의 선형탐색만 하면 되기 때문에 B-Tree에 비해 빠릅니다.(B-Tree는 모든 노드를 탐색해야함.)
• 풀 스캔이 아니더라도 부등호를 이용한 순차검색에도 유리합니다. 시작 지점을 먼저 찾고 Linked List로 연결된 리프노드를 종료지점까지 순회하면 됩니다.

B+Tree 단점

• B-Tree일 경우 최상의 경우 Root Node에서 값을 찾고 끝낼 수 있지만, B+Tree는 데이터가 Leaf node에 위치해 있기 때문에 Leaf Node까지 갈 수 밖에 없습니다.