문제 풀이

트리의 중위 순회 후위 순회를 입력 받아서 전위 순회의 결과를 출력하는 문제
분할 정복으로 풀이를 한다.
위 트리에서 후위 순회로 각 서브트리에 대해서 마지막 원소는 트리의 부모 노드가 된다.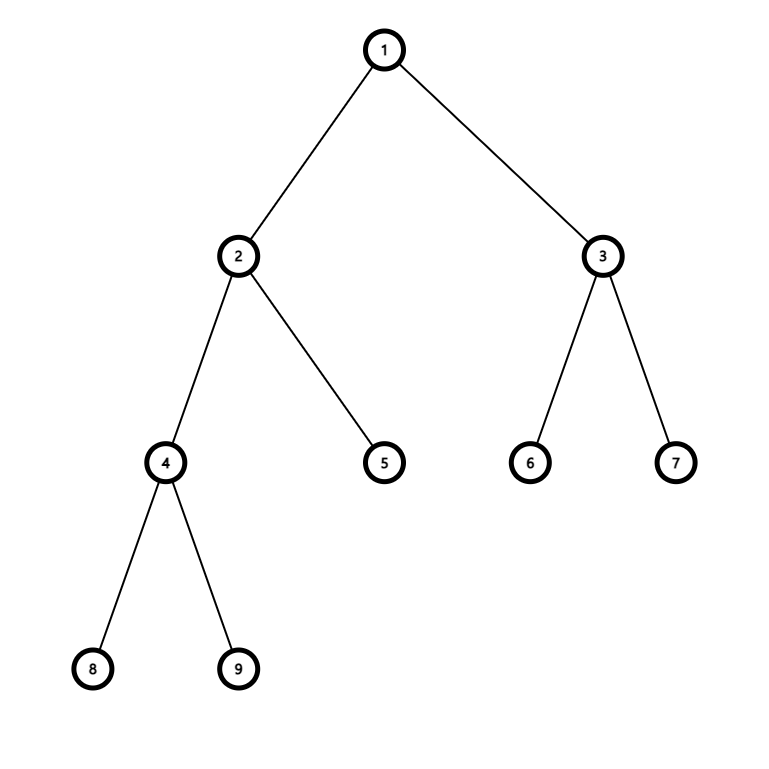
ex) 후위 순회 - 8 9 4 5 2 6 7 3 (1) <- 부모 노드이자 루트노드
후위 순회에서 찾은 부모 노드를 이용해서 중위 순회에서 왼쪽, 오른쪽 서브 트리를 구할 수 있다.

위 트리에서 중위 순회의 결과는 8 4 9 2 5 (1) 6 3 7로 방금 찾은 부모 노드를 이용해
왼쪽 서브트리 8 4 9 2 5, 오른쪽 서브트리 6 3 7을 찾을 수 있다.
그러면 다시 후위 순회 결과에서 왼쪽 서브트리와 오른쪽 서브트리를 찾고 각각 맨 오른쪽 원소가 부모노드임을 알 수 있다.
후위 순회에서 서브트리를 나누는 법은 중위 순회에서 부모노드를 기준으로 위의 예에서는 왼쪽 서브트리의 노드가 5개 오른쪽 서브트리의 노드가 3개 (parent_idx - inorder_start, inorder_end - parent_idx)이므로
다음 왼쪽 서브트리의 후위 순회는 post_start 부터 post_start + left_size({8, 4, 9, 5 , 2} 5개),
다음 오른쪽 서브트리의 후위 순회는 post_start 부터 post_end - 1({6, 7, 3} , 3개)까지다.
반복 해서 시작지점이 끝점보다 뒤로갈 경우는 함수를 종료해주고 pre함수 시작할 때 각 서브트리에서 후위 순회의 마지막 노드를 출력하면 된다.

문제 링크

boj/2263

소스코드

PS/2263.cpp

#include<iostream>
#include<vector>
#include<queue>
#include<algorithm>
#include<memory.h>
#include<math.h>

using namespace std;

int in[100001];
int post[100001];
int idx[100001];
void pre(int in_s, int in_e, int post_s, int post_e);

int main()
{
	ios_base::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int n;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> in[i];
		idx[in[i]] = i;
	}
	for (int i = 0; i < n; i++)
		cin >> post[i];
	pre(0, n - 1, 0, n - 1);

}
void pre(int in_s, int in_e, int post_s, int post_e)
{
	
	if (post_s > post_e ||in_s > in_e)
		return ;

	int i = idx[post[post_e]];
	cout << in[i] << ' ';
	int left = i - in_s;
	pre(in_s, i - 1, post_s, post_s + left - 1);
	pre(i + 1, in_e, post_s +  left, post_e - 1);
}