문제 풀이

10^16을 2진수로 바꿨을때 55자리의 2진수로 바뀐다.
배열 d는 자리수가 i+1개인 2진수의 1의개수의 누적합이다. (i == 2일 경우 3자리 2진수 까지의 1의 개수 누적합)

1자리는 1 하나로 d[0] = 1
2자리는
10
11
d[1] = 1 + 3

3자리는
100
101
110
111
d[2] = 8 + 4

그러므로 n 자리는
d[n-1] = d[n-2] * 2 + 2^(n-1)

이렇게 누적합을 모두 구하고 나면 특정 숫자까지의 1의 개수의 누적합을 구할 수 있다.

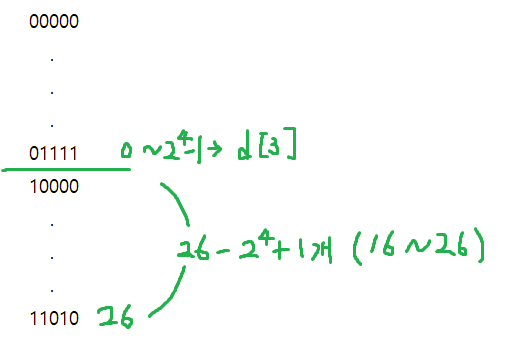
26을 예로 들었을 때 오른쪽 부터 시작해서 맨 끝인 5번째 자리수가 1이므로 4자리의 수 까지의(0 ~ 15) 1의 개수는 모두 더해져야하고 -> d[3]
그 뒤는 10000부터 11010 까지 11개의 숫자가 있으므로(16 ~ 26) 일단은 5번째 자리가 모두 1이므로 11이 더해져야한다
4번째 자리, 3번째 자리 ... 1번째 자리 까지 계산하면 n까지의 1의 개수의 합을 구할 수 있다.

---

for (int i = v.size() - 1; i >= 0; i--)
	{
		if (v[i] == 1)
		{
			ans += d[i - 1]+n - ((long long)1<<i) + 1;
			n -= ((long long)1 << i);
		}
	}

---

n1부터 n2까지의 1의 개수의 합을 구하려면
(n2까지의 1의 개수 합) - (n1 - 1까지의 1의 개수 합)을 해주면된다.

문제 링크

boj/9527

소스코드

PS/9527.cpp

#include <string>
#include <vector>
#include<iostream>
#include<memory.h>
#include<map>
#include<algorithm>
#include<queue>
#include<set>
#include<math.h>
using namespace std;
long long d[56];

long long solution(long long n);
int main()
{
	ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);
	d[0] = 1;
	long long n,n2;
	cin >> n>>n2;
	for (int i = 1; i <= 55; i++)
	{
		d[i] = d[i - 1] * 2 +((long long)1<<i);
	}
	cout << solution(n2)-solution(n-1)<<'\n';
}
long long solution(long long n)
{
	vector<int> v;
	long long tmp = n;
	while (tmp != 0) {
		v.push_back(tmp % 2);
		tmp /= 2;
	}
	long long ans = 0;
	for (int i = v.size() - 1; i >= 0; i--)
	{
		if (v[i] == 1)
		{
			ans += d[i - 1]+n - ((long long)1<<i) + 1;
			n -= ((long long)1 << i);
		}
	}
	return ans;
}