Divisor, multiple, division algorithm
만약 정수 a,b,m이 있을 때 어떠한 m 에 대하여 a = mb이면 0이 아닌 정수 b는 a를 나눈다.
b|a라 표현 가능하며 b를 a의 divisor라 한다. 또한 a를 b의 multiple이라 한다.
속성
- 만약
a|1이면a = ±1이다. - 만약
a|b이고b|a이면a = ±b이다. - 0은 모든 정수의 배수이다. 즉 모든 정수는 0의 약수이다.
- 만약
a|b이고b|c이면a|c이다. - 만약
b|g이고b|h이면b|(mg + nh)이다.
Division Algorithm
a를 n으로 나눈 몫을 q, 나눈 나머지를 r이라 할 때
즉 a = qn + r 일 때 0 ≤ r < n이다.
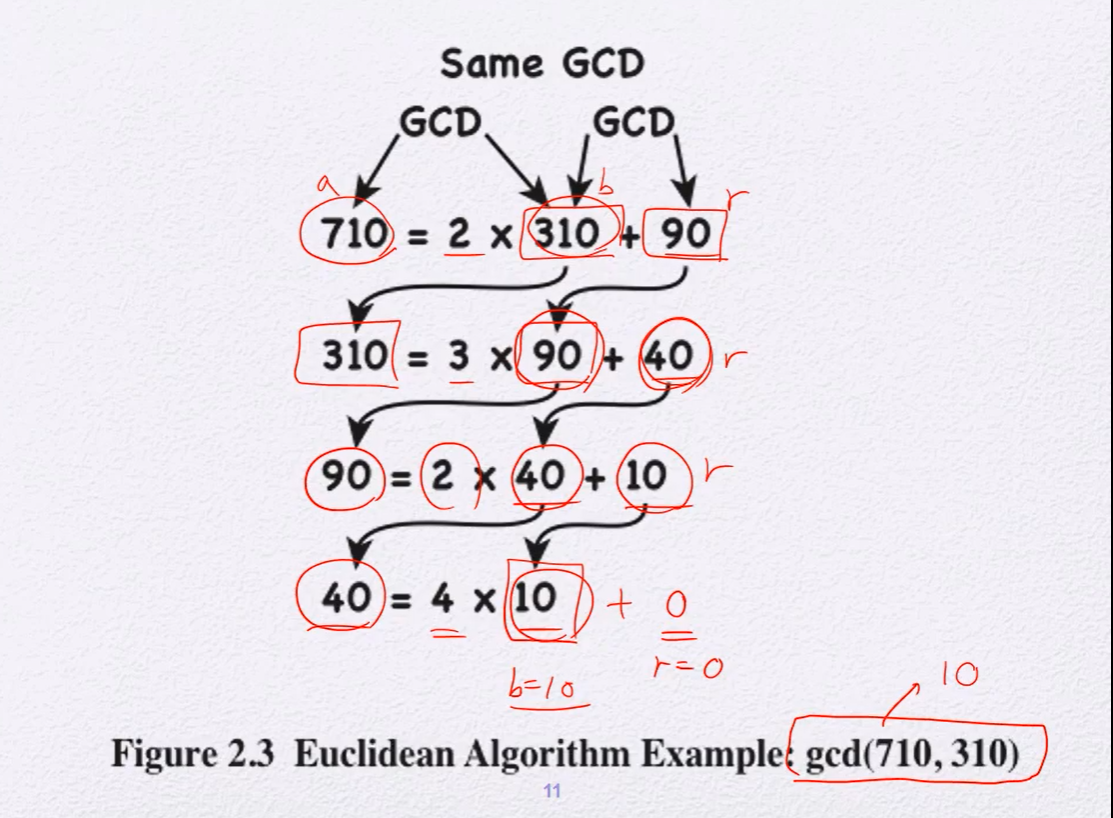
GCD and Euclid algorithm
gcd(a, b) 는 a와 b의 최대 공약수
- gcd(0, 0) = 0
- c가 a와 b의 최대공약수이다. 의 의미
c는 a와 b의 divisor다.
a와 b의 divisor 들은 c의 divisor이다.
Modular arithmetic
만약 정수 a와 양의 정수 n이 있을 때 a mod n을 a를 n으로 나눈 나머지를 구하는 연산이라 하고 이 때의 n을 modulus라 한다.
ex) 11 mod 7 = 4; -11 mod 7 = 3;
만약 a mod n = b mod n이면 a와 b를 congruent(합동)이라 하고 a ≡ b (mod n)이라 쓴다.
congruent 속성
a ≡ b (mod n)과n | (a - b)는 같은 의미이다.a ≡ b (mod n)이면b ≡ a (mod n)이다.a ≡ b (mod n)이고b ≡ c (mod n)이면a ≡ c (mod n)이다.
Modular arithmetic 속성
[(a mod n) + (b mod n)] mod n = (a + b) mod n[(a mod n) - (b mod n)] mod n = (a - b) mod n[(a mod n) * (b mod n)] mod n = (a * b) mod n- 교환, 결합, 분배 법칙이 성립한다.
- 항등원이 존재한다.
- 덧셈의 역원이 항상 존재한다.
- 곱셈의 역원은 항상 존재하지는 않는다.
Extended Euclid algorithm and multiplicative inverse
modulus의 곱셈에 대한 역원이 존재하려면 modulus와 서로소 관계이어야 한다.
Extended Euclid algorithm
a와 b (a > b)가 주어질 때 ax + by = d = GCD(a, b)에서 x, y를 찾는 알고리즘이다.
d가 1이 될 때의 y가 b mod a의 곱셈에 대한 역원이 된다.
Prime numbers
1과 자기자신만 약수로 가지는 수
Fermat (little)theorem
소수 p와 p와 서로소인 a(a는 양의 정수)가 있을 때
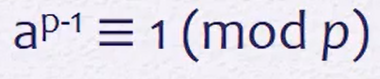
소수 p와 양의 정수 a가 있을 때
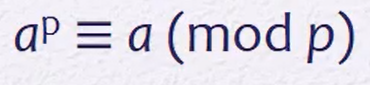
Euler totient function Φ(n)
n까지의 수 중에 n과 서로소인 갯수를 Φ(n)라 한다.
- 소수 p가 있을 때
Φ(p) = p - 1이다. - n = p * q (p, q는 소수)일 때
Φ(n) = (p - 1)(q - 1)이다.
Euler theorem
서로소인 a, n에 대해서
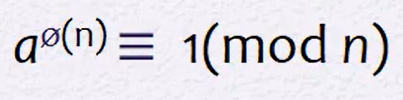
Primality test
Trial division
루트 n까지 다 나눠보기
Fermat test
페르마의 소정리를 이용하여 n과 gcd가 1이 되는 a를 뽑아 내어 n을 p에 대입 했을 때 1이 안나오면 소수가 아니다.
Miller-Rablin test
위의 Fermat testdhk NSR test를 같이 돌린다.

Deterministic algorithm
trial division보다는 효율적이지만 MR보다 훨씬 느려서 아직 쓰이지 않는다.
Hybrid
example: Trial division + MR/Fermet
Powers of integers modulo p and group generator
페르마의 소정리를 만족하는 p-1제곱 전에 1이 안나오게 하는 a를 generator라 한다.
Discrete logarithm
어떤 Primve Number p가 있고, 0이 아닌 정수 α, β가 존재한다고 했을 때,
β ≡ α^x (mod p)
여기서, x를 구하는 것을 discrete logarithm 문제라고 한다. 여기서, α^n ≡ 1 (mod p)라고 했을 때, n이 이것을 만족하는 가장 작은 양의 정수라면, 0 ≤ x < n이며, 여기서
x = Lα(β)
이것을 α를 밑으로 가지는 β의 discrete logarithm이라 한다.
Integer Factorization
엄청 큰 수의 소인수분해를 구하는 것은 엄청난 연산이 필요하다.
현재 공개키 암호를 설계할 때는 위의 Discrete logarithm과 Integer Factorization를 기반한다.
하지만 퀀텀 컴퓨터가 나온다면 깨질 수 있다.
출처: Cryptography and Network Security: Principles and Practices
