Finite field arithmetic
Finite field를 block cipher에서 왜 사용하는가?
-
AES를 구성하는 함수들
- Substitution
- Transposition (permutation)
- Multiple rounds
- Simple bit operations (XOR 같은 )
-
Bit randomizion effect
Field multiplication이나 Field inversion이 이런 randomizion effect이 가능하다.
덧셈은 randomizion 효과가 없다.
곱셈이나 역연산으로 복잡도를 증가시킬 수 있다.
Binary Field의 근거
-
우리는 편의성과 구현 효율성을 위해 낭비되는 비트 패턴이 없는, 주어진 수의 비트에 정확히 맞는 정수로 작업을 하고 싶다.
즉, (mod 2^n)을 해서 0부터 (2^n-1)까지 쓰려고 한다. -
하지만 2^n을 modulus로 쓰게 되면, 이런 modular연산에 대해서는 field를 구성할 수 없다.
-
즉, 이런 수(예: 2^3=8)를 정수 그대로 쓸 수는 없고, 이거를 binary field로 바꿔서, 모든 원소들을 숫자가 아닌 계수가 2진수인 다항식으로 표현하면 잘 연산할 수 있다.
-
GF(2^n)에 속하는 모든 다항식은 n-bit로 표현할 수 있다.
AES에 대한 Finite Field Arithmetic
-
Advanced Encryption Standard(AES)를 위해 우리는 GF(2^8)를 사용한다.
모든 연산은 8-bit bytes 단위이다. -
finite field GF(2^8)를 쓰기 때문에, irreducible polynomial이 필요하다.
irreducible polynomial: x^8+x^4+x^3+x+1
AES structure
plaintext, ciphertext, intermediate data 모두 4x4 matrix of bytes 구조의 state를 가진다.
파라미터로 들어오는 key size는 128, 192, 256 bits이다.
셋 중 하나 선택해서 사용하면 되는데, key 길이가 길어지면 안전해지지만 연산 속도는 느려지게 된다.
SPN(Substitution-permutation network)
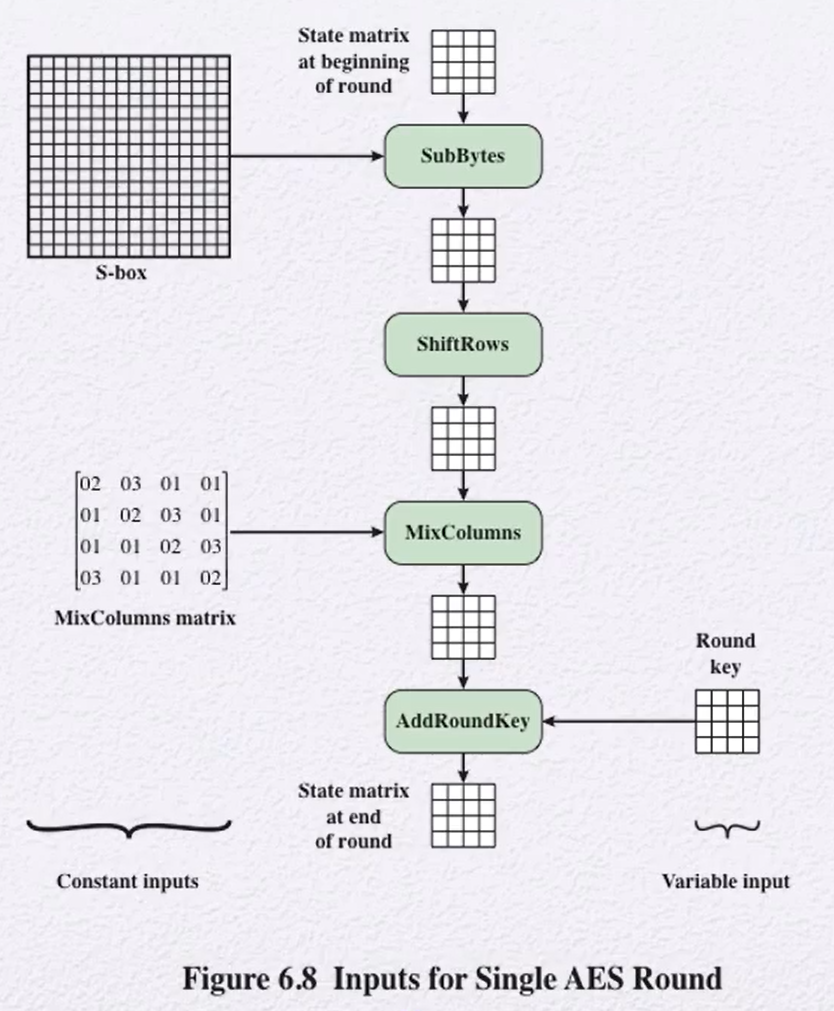
하나의 round에서 4개의 연산이 이루어진다.
Permutation: ShiftRows
Substitution: SubBytes / MixColumns / AddRoundKey
AES는 복호화할 때, 암호화 과정을 역으로 올라간다. 이를 위해 모든 연산은 역연산이 존재한다.
AES Parameters
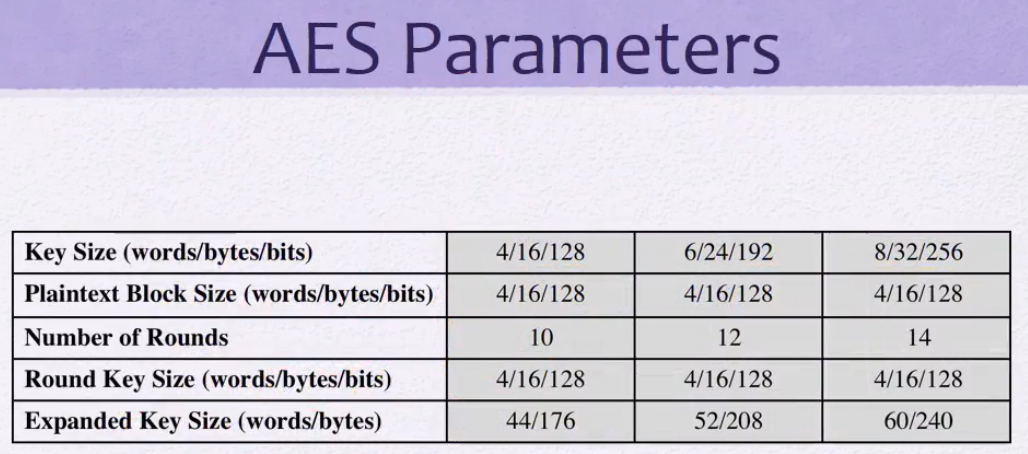
- subkey의 개수 = 라운드의 개수 + 1
AES transformation function
SubBytes
S-box를 이용해서 byte끼리의 대치를 수행
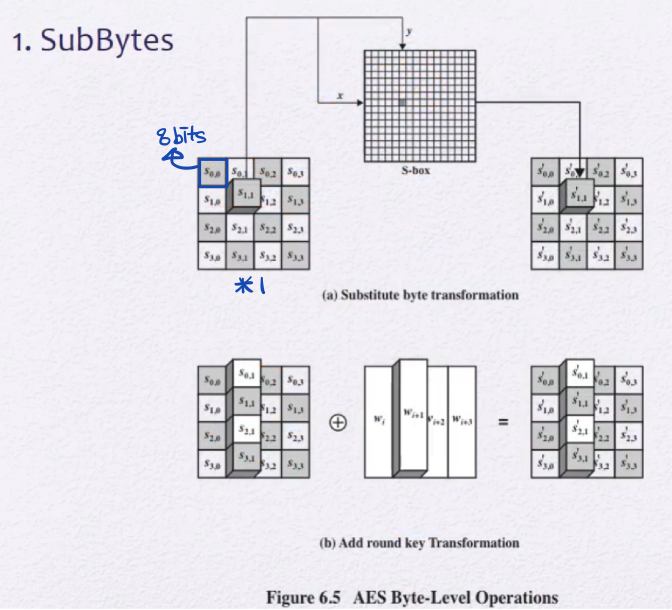
- S-box를 사용하는 이유
- linear하지 않은 수학적 함수인 곱셈에 대한 역원을 이용해 상관관계를 줄인다.
Shift Rows
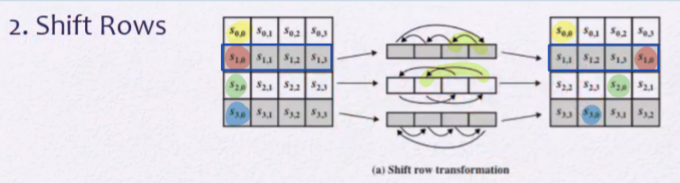
- 입력의 하나의 열이 출력의 모든 열에 영향을 끼치게 된다.
Mix Columns
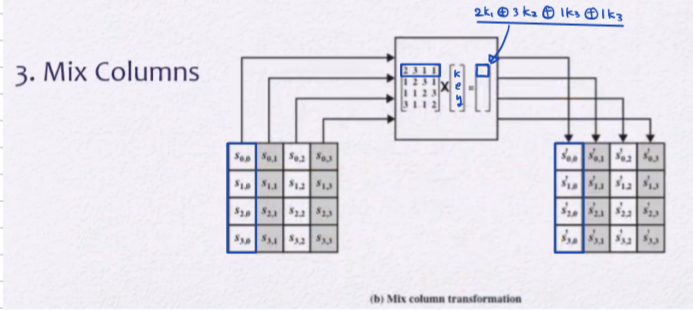
- 각 열이 행렬 곱 연산을 통해 새로운 값을 가지게 된다.
AddRoundKey
- state의 128 bits가 round key의 128 bits와 XOR 된다.
AES의 포인트
- 입력의 일부분이 출력의 여러 부분에 분산해서 영향을 미치게 한다.
- 입출력 사이 관계가 자명하게 드러나지 않도록 한다.
Decryption
마지막 라운드 key부터 이용하여 각 연산의 역연산을 수행한다.
AES key expansion
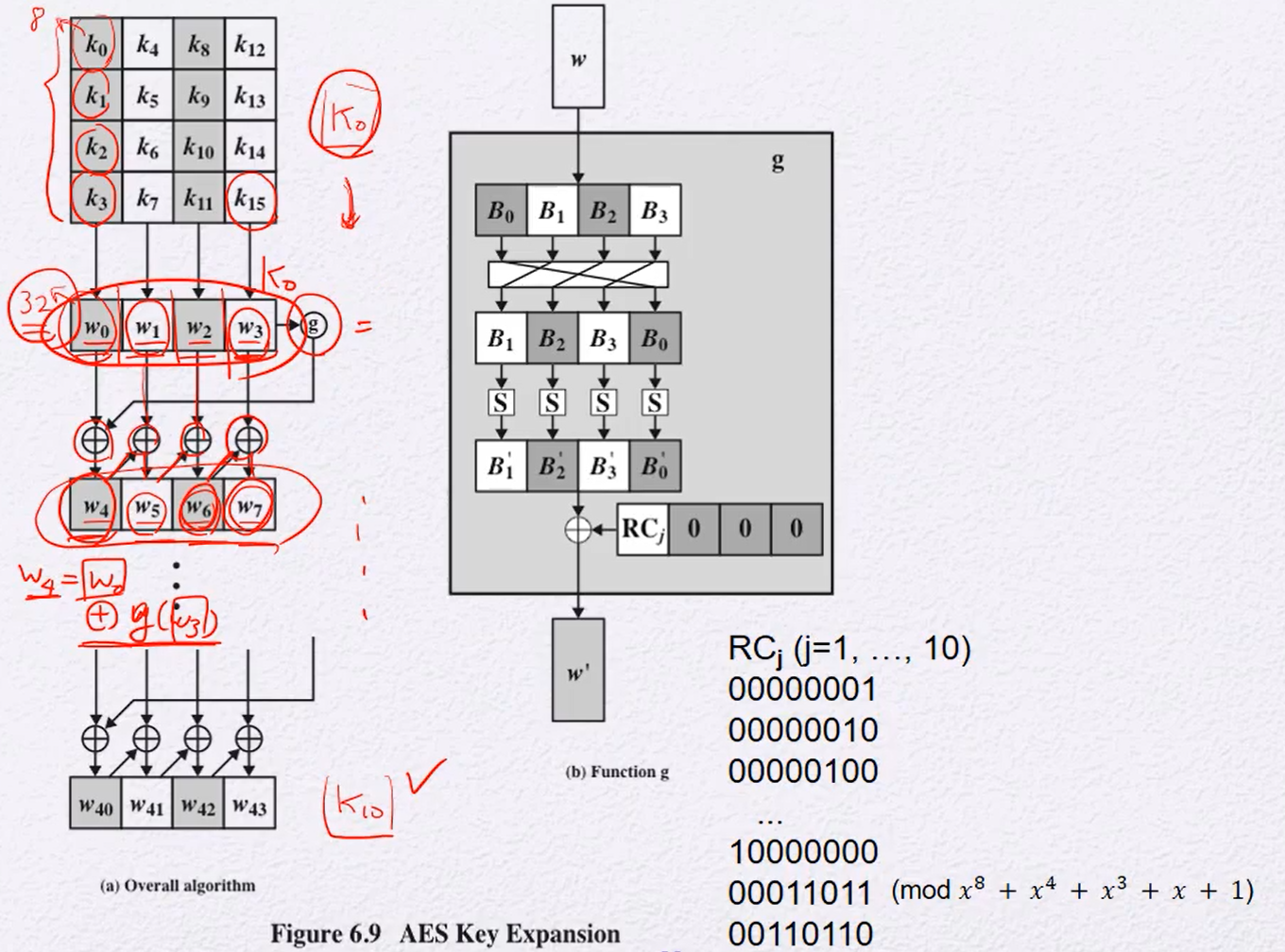
(w[0]~w[3]), (w[4]~w[7]), ... 들이 각각 subkey이다.
w4=w0 XOR g(w3)
RCj -> 어떤 상수
cipher key의 diffusion이 round key에 적용이 된다.
diffusion: 한 bit가 다른 여러 곳에 영향을 준다. (확산)
출처
https://hororolol.tistory.com/451?category=897521
[Cryptography and Network Security: Principles and Practices]
