안녕하세요! 오늘은 스탠포드 대학교 cs231n 강의 2번째 Chapter 두 번 째 정리 입니다!
"Linear Classification"
Linear Classification?
선을 이용하여 집단을 두 개 이상으로 분류하는 것
Linear Classification은 앞으로 보게 될 다양한 종류의 딥러닝 알고리즘들의 기본이 되는 아주 간단한 알고리즘입니다.
Linear Classification은 NN과 CNN(Convolutional Neural Network)의 기반 알고리즘이기 때문에 동작 원리를 정확히 이해하는 것이 중요합니다.
CIFAR-10 데이터를 다시 상기시켜 보면,

CIFAR-10 데이터셋에는 50,000여개의 train sample이 있으며, 각 이미지는 32x32 픽셀을 가진 3채널 컬러 이미지입니다.
K-NN과 비교
Linear Classification은 K-NN과 조금 다른 방식으로 접근합니다.
"Parametric approach"
앞서 K-NN은 파라미터가 없었습니다. 그저 "전체" train 데이터를 가지고 있었고, 전체 train 데이터를 테스트에 사용했습니다.
하지만 parametric approach에서는 train 데이터의 정보를 "요약"합니다. 그리고 그 요약된 정보를 파라미터 W에 모아줍니다. 이러한 방식을 사용하면 테스트를 할 때 더이상 train 데이터가 필요하지 않습니다. 오직 W만 있으면 됩니다.
그러니 이 함수의 구조를 적절하게 잘 설계하는 것이 중요합니다. 어떤 식으로 가중치 W와 데이터를 조합할 지 여러가지 복잡한 방법으로 생각해볼 수 있는데, 이러한 일련의 과정들이 모두 다양한 NN(Neural Network) 아키텍쳐를 설계하는 과정입니다.
가중치 W와 데이터 X를 조합하는 가장 쉬운 방법은 W와 X를 곱하는 것입니다.
이 방법이 바로 Linear Classification입니다.
F(x,W) = Wx + b
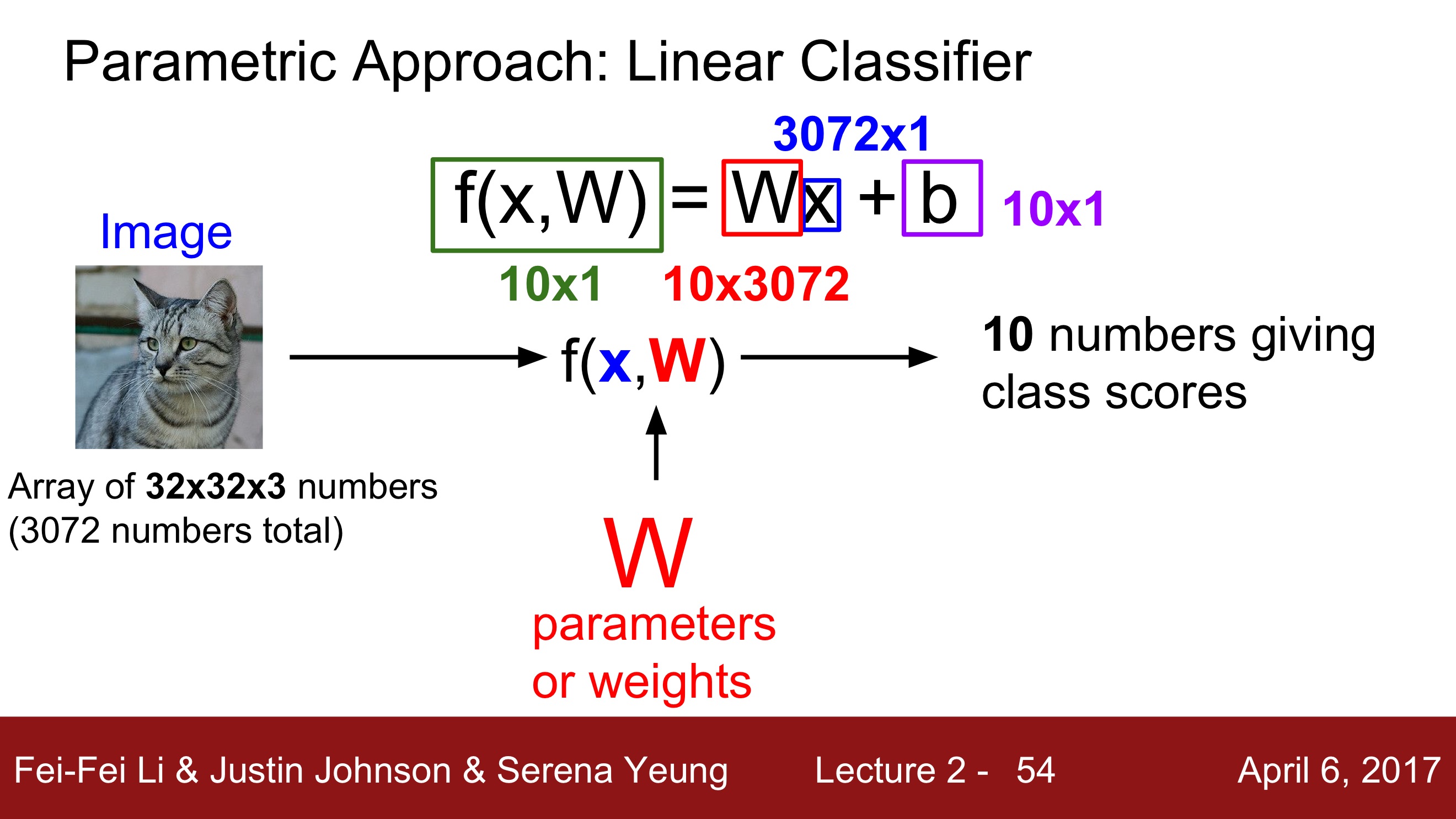
Linear Classification은 입력이미지(X)와 가중치(parameter, W)를 가지고 10개의 스코어를 출력합니다. 이 때, 10개의 숫자는 구분해야할 카테고리의 스코어입니다.
출력되는 숫자의 개수 = 구분해야하는 카테고리 개수
카테고리의 스코어가 높을 수록 그 카테고리에 해당할 확률이 높다는 걸 의미합니다.
ex. 클래스가 4개 일 때 각각의 스코어가 다음과 같을 경우,
고양이 1.9
강아지 0.4
비행기 1.12
말 0.8
해당 이미지는 고양이일 확률이 가장 높으므로 고양이로 분류됩니다.
위의 자료를 보면, 입력 이미지는 32x32x3이므로
이 값을 길게 펴서 열벡터로 만들면 3072x1 차원의 벡터가 됩니다.
이 3072차원의 벡터가 10개의 스코어가 되어야 하므로
W는 10x3072 가 되어야 합니다.
W x X + b = 10 scores (열벡터)
[10 x 3072] x [3072 x 1] = [10 x 1] + [10 x 1]
가끔은 bias term도 같이 더해주기도 합니다.
bias term은 10차원의 열벡터로 입력(이미지)과 직접적으로 연결되지 않습니다.
대신에 데이터와 무관하게 특정 클래스에 우선권을 부여합니다.
예를 들어 데이터 셋에 고양이 데이터보다 강아지 데이터가 훨씬 많을 경우,
고양이 클래스에 상응하는 bias가 더 커지게 됩니다.
( 이 부분은 고양이 데이터가 훨씬 적기 때문에 '고양이' 카테고리 스코어가 너무 작게 나올 수도 있으니 bias를 크게 주어 예측의 정확도를 높이는 것으로 이해했습니다! )

이 페이지를 보면(3가지 클래스로 예측),
1) 맨 왼쪽 입력 이미지(2x2)를 받아 쭉 펴서 4차원의 열벡터로 만듭니다.
2) 가중치 행렬(W)은 3x4 행렬이 되며
3) bias는 데이터와 독립적으로 각 카테고리에 연결됩니다.
위의 과정을 거친 '고양이 스코어'는 입력 이미지의 픽셀 값들과 가중치 행렬을 내적한 값에 bias를 더한 값입니다.

하단의 10개의 이미지는 10개의 카테고리에 해당하는 행벡터를 시각화한 것입니다.
맨 왼쪽의 이미지는 비행기(airplane)에 해당하는 템플릿 이미지로,
전반적으로 파란색을 띄고 있습니다.
이 이미지를 해석해보면 Linear Classifier가 비행기를 분류할 때 푸르스름한 것을 찾고 있다는 것을 알 수 있습니다. 하지만 비행기처럼 생기진 않았습니다.
이는 Linear Classifier의 문제점으로 들 수 있는데요.
한 클래스 내에 다양한 특징들이 존재할 수 있지만,
모든 특징을 평균화시키기 때문에 다양한 모습이 있더라도
각 카테고리를 인식하기 위한 템플릿은 단 하나밖에 없습니다.

Linear Classifier를 또다른 관점으로 해석할 수 있습니다.
이미지를 고차원의 한 점으로 보는 것입니다.
Linear Classifier는 각 클래스를 구분시켜 주는 선형 결정 경계 역할을 합니다.
왼쪽 상단 비행기의 경우 Linear Classifier는 파란색 선을 학습해서 비행기와 다른 클래스를 구분할 수 있습니다.
이러한 접근에도 문제점이 존재할 수 있습니다.

맨 왼쪽 그림은 두 개의 클래스(빨간색, 파란색)를 가진 데이터 셋입니다.
파란색 카테고리는 0보다 큰 픽셀이 홀수개인 경우이고,
빨간색 카테고리는 0보다 큰 픽셀이 짝수개인 경우입니다.
좌표 평면에 이 같은 규칙으로 그려보면 두 개의 사분면에는 파란색 카테고리,
나머지 두 개의 사분면은 빨간색 카테고리입니다.
이 데이터를 선 하나로 분류할 방법은 없습니다. 여기서 말하는 선은 직선을 뜻합니다!
이러한 경우는 현실에선 영상 내 동물이나 사람의 수가 홀/짝수인지 분류하는 문제로 표현될 수 있습니다.
맨 오른쪽 그림은 빨간색 배경에 파란색의 세 점이 있습니다.
한 클래스가 다양한 공간에 분포할 수 있으며 이럴 경우 Linear Classifier로 이 문제를 해결할 순 없습니다.
이번 챕터를 요약해보면,
-
Linear Classifier가 단순히 행렬과 벡터 곱의 형태
-
템플릿 매칭과 관련있으며 각 카테고리에 대해 하나의 템플릿을 학습
-
가중치 행렬 W를 학습시키고나면 새로운 학습 데이터에도 스코어를 매길 수 있음
위와 같은 내용을 배웠습니다.
이번 포스팅으로 Lecture 02의 내용을 마무리합니다! 이번 포스팅도 읽어주셔서 감사합니다 ~~! 이해에 도움이 되었길 바랍니다 !

