문제 - 11053

문제접근

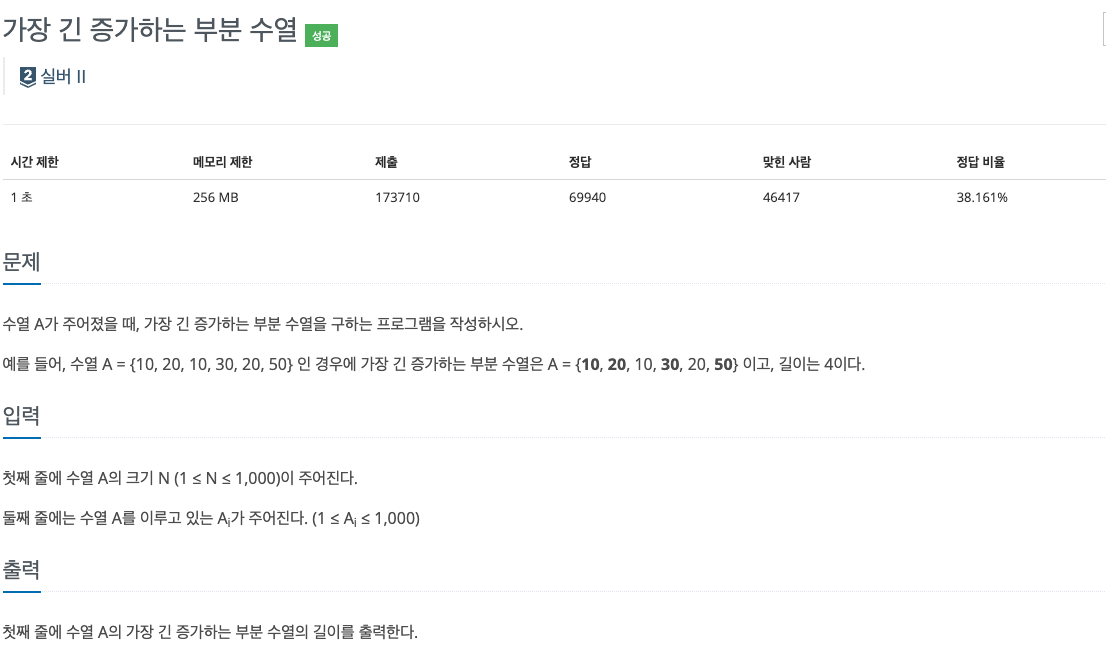
최장 증가 부분 수열의 알고리즘을 사용했다. dp를 이용해서 O(N^2)의 시간복잡도를 가지고 있다.
1. 규칙성을 위해서 A[0] = 0 으로 설정하여 dp배열과 인덱스를 맞춰줬다.
2. A[0] ~ A[i - 1]을 탐색하며 A[i]보다 작은 A[j]를 가지는 j들 중 가장 큰D[j] 찾기
3. 가장 작은 값의 dp[j] + 1을 해서 증가하는 부분 수열의 길이를 계속 탐색한다.

소스코드

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        int N = sc.nextInt();

        int A[] = new int[N+1];
        for (int i = 1; i <= N; i++) {
            A[i] = sc.nextInt();
        }

        int dp[] = new int[N+1];
        dp[0] = 0;

        for(int i = 1; i <= N; i++) {
            //이전 값에서 가장 작은값 찾기
            int temp = 0;
            for(int j= i-1; j >= 0; j--) {
                if(A[i] > A[j]) {
                    temp = Math.max(temp, dp[j]);
                }
            }
            dp[i] = temp +1;
        }

        int ans = 0;
        for(int i = 1; i <= N; i++) {
            ans = Math.max(ans, dp[i]);
        }
        System.out.println(ans);
    }
}