오늘은 마가리타 한 잔? [P5]

문제: https://www.acmicpc.net/problem/2728

분류

• 다이나믹 프로그래밍

✔ 풀이과정

dp[v+1][money+1] 크기의 배열을 만듭니다.
dp[i][j] 는 i번째 가판대 까지 봤을 때 정확히 j만원으로 살수 있는 조합의 수 입니다.
d[0][0] = 1로 해두고 각 가판대마다 그 마가리타를 샀을 때와 안샀을 때의 조합을 각각 추가합니다.

for (int i = 0; i < V; i++)
{
	for (int j = 0; j <= D; j++)
	{
		dp[i + 1][j] += dp[i][j]; //안 산 경우
		if (j + shop[i] <= D) //샀을 경우, 돈이 초과하는 경우는 제외
		{
			dp[i + 1][j + shop[i]] += dp[i][j];
		}
	}
}

이렇게 하면 dp[v]에는 0~money까지의 금액으로 살 수 있는 경우의 수가 각각 위치에 들어있을 겁니다.

그런데 현재상황에선 어떤 경우가 정답에 해당하는 케이스인지 알 수 없습니다.
심지어 같은 가격으로 살 수 있는 경우의 수도 남는 돈이 있는 경우와 아닌 경우가 섞여 있을 겁니다.
도대체 어떻게 구별해야 할까요?

힌트는 전체 경우의 수를 특정 마가리타가 포함되어 있는 경우와 아닌경우를 나눌 수 있다는 점에 있습니다.

예제를 하나 들면서 설명하겠습니다.
가판대가 4개있고 각각 1, 1, 2, 4 만원 인 케이스 입니다.
위의 dp식을 이용하여 배열을 채우면 다음과 같은 그림이 됩니다.

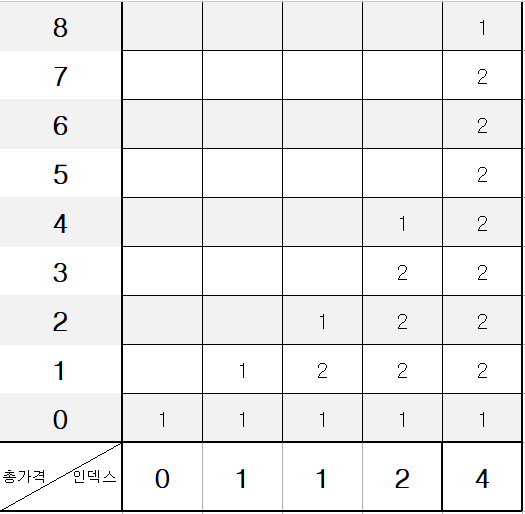
(인덱스라고 썼지만 가격을 표시했으니 유의해서 봐주세요.)
마지막 칸이 전체 경우의 수인데요, 이를 2짜리 마가리타를 포함한 경우와 아닌경우로 나눠 보겠습니다.

우선 맨처음 0원칸은 당연히 2가 미포함 된 것이겠죠?
해당 경우는 1,1,2,4를 모두 미포함 한 경우인데 여기서 2를 포함하는 것으로 바꾸면 2만원이 되겠네요.

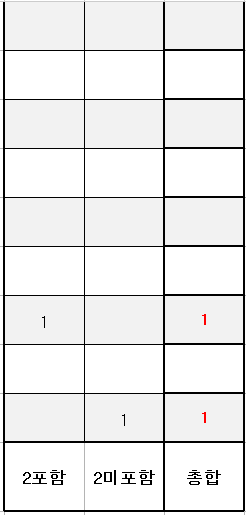
그 다음 1만원 칸도 2가 미포함 된 경우입니다. -1만원에서 2만원을 포함시킨건 아닐테니까요.
여기서 2만원을 포함 시킨 3만원 칸에 해당 경우만큼 추가해줍니다.

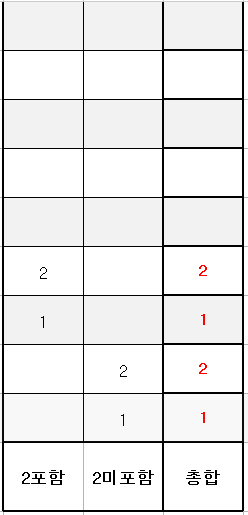
그 다음 2만원 칸을 봅시다. 이미 2만원을 포함시킨 경우가 1가지 있네요. 그럼 2-1 = 1 가지 경우가 2만원을 미포함한 케이스 겠군요. 앞에서 한대로 표를 채워봅시다.

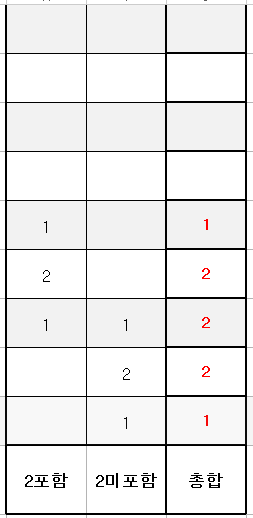
이제 감이 오셨을 테니 나머지도 채워볼까요.

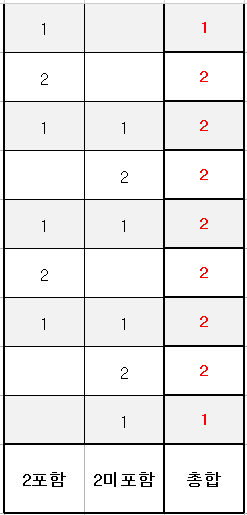
짜잔~ 전체 경우의 수와 딱 맞게 나왔습니다.

특정 마가리타가 포함된 경우를 include, 미포함 된 경우를 exclude라고 하겠습니다.
include는 exclude에서 왔다고 볼 수 있는데요, 이를 생각해보면 exclude에서 include로 갈 수 있는 경우는 돈이 남는 경우라고 볼 수 있습니다.
전체 경우에서 이러한 경우를 빼면 답을 구할 수 있습니다.

결론적으로 풀이 방법은 다음과 같습니다.
1. 마가리타를 오름차순으로 정렬 한 후, 전체 경우의 수를 첫 마가리타에 대해 include와 exclude로 분리합니다(가지고 있는 돈보다 큰 금액은 include에 넣지 않습니다).
2. include에 포함된 갯수 만큼 total에서 뺍니다.
3. 다음 마가리타에 대해서 include를 다시 include와 exclude로 분리합니다.
4. 반복...
5. 처음부터 아무 마가리타도 살 수 없을 때 total = 0 으로 예외처리를 해줍니다. 그렇지 않으면 dp[0][0]으로 1이 나와버립니다.

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

long long dp[31][1001];
vector<int> shop;
long long include[1001];
long long exclude[1001];

int main()
{
	long long T, V, D,tmp;
	long long total;
	scanf("%lld", &T);
	while (T--)
	{
		total = 0;
		for (int i = 0; i < 31; i++)
		{
			for (int j = 0; j < 1001; j++)
			{
				dp[i][j] = 0;
			}
		}
		for (int j = 0; j < 1001; j++)
		{
			include[j] = 0;
			exclude[j] = 0;
		}
		dp[0][0] = 1;
		scanf("%lld %lld", &V, &D);
		for (int i = 0; i < V; i++)
		{
			scanf("%lld", &tmp);
			shop.push_back(tmp);
		}
		sort(shop.begin(), shop.end());
		for (int i = 0; i < V; i++)
		{
			for (int j = 0; j <= D; j++)
			{
				dp[i + 1][j] += dp[i][j];
				if (j + shop[i] <= D)
				{
					dp[i + 1][j + shop[i]] += dp[i][j];
				}
			}
		}

		for (int k = 0; k <= D; k++)
		{
			total += dp[V][k];
			exclude[k] = dp[V][k];
		}
		
		for (int i = 0; i < V; i++)
		{
			for (int k = 0; k <= D; k++)
			{
				if (k + shop[i] <= D)
				{
					include[k + shop[i]] += exclude[k];
					exclude[k + shop[i]] -= exclude[k];
					total -= exclude[k];
				}
			}
			for (int k = 0; k <= D; k++)
			{
				exclude[k] = include[k];
				include[k] = 0;
			}
		}
		if (shop[0] > D)
		{
			total = 0;
		}
		printf("%lld\n", total);
		while (!shop.empty())
		{
			shop.pop_back();
		}
	}
}

각 테스트 케이스마다 시간복잡도는 O(VD+VlgV)가 되겠네요