[백준 - 16566] 카드게임
문제: https://www.acmicpc.net/problem/16566
거의 유니온 파인드처럼 구현해서 풀었다. 이진 탐색을 쓰지 않으므로 더 빠를 수도 있을 것 같다.
숫자가 400만까지 밖에 등장하지 않으므로 400만의 크기를 가지는 두 배열을 만들었다.
하나는 해당 숫자의 카드가 존재하는지 나타내는 배열이고,
다른 하나는 해당 숫자보다 큰 카드의 index를 가르키는 배열이다.
각 배열을 card, ptr 라고 하겠다.
처음 card를 입력받고 다음 코드를 수행하면서 ptr 배열을 완성 시킨다.
for(int i=n;i>=0;i--)
{
if(card[i+1])
ptr[i] = i+1;
else
ptr[i] = ptr[i+1];
}현재 ptr 배열은 존재하는 카드 중에서 i 보다 크면서 가장 작은 카드를 가르키고있다. 이 배열이 유니온 파인드 풀이의 이진탐색을 대체한다.
철수가 낸 카드(=input)를 입력 받으면 ptr 배열을 따라가서 해당 카드를 출력하고 그 위치의 card를 false로 만든다. 그 후 ptr[input] 은 방금 도착한 위치로 업데이트 해준다. 유니온 파인드에서 parent를 업데이트 하는 것과 비슷하다.
주의해야 할 점은 카드를 없애기 때문에 ptr 배열 한번에 카드가 있는 곳까지 도달하지 않는 경우도 있으므로, card[현재위치] 가 true가 될 때 까지 따라가야한다.
[백준 - 1007] 벡터 매칭
문제: https://www.acmicpc.net/problem/1007
두 점A,B를 골라서 만드는 벡터는 A-B 혹은 B-A로 표현 할 수 있다는 점만 알면 풀이를 생각할 수 있다(그나저나 벡터 표현을 쓸 방법을 모르겠다).
N개의 점으로 N/2개의 벡터를 만든다면 N개의 점 중에서 N/2개를 골라 +를 붙이고, 나머지는 -를 붙인다는 것을 알 수 있다.
20개중에서 10개를 고르는 경우의수가 20만이 안되므로 브루트포스로 풀면 된다.
[백준 - 2243] 사탕상자
문제:https://www.acmicpc.net/problem/2243
사탕의 맛이 100만까지기 때문에 100만크기의 세그먼트 트리를 썻다.
기존에 사용하던 세그먼트 트리 update를 쓰고, 사탕을 하나 꺼내는 pop 함수를 만들어 풀었다.
ll sTreePop(int node, int start, int end, int i)
{
if (start == end)
{
sTreeUpdate(1,1,1000000,start,-1);
return start;
}
else
{
if(sTree[node*2] >= i)
return sTreePop(node*2,start,(start + end) / 2,i);
else
return sTreePop(node*2+1,(start + end) / 2+1,end,i-sTree[node*2]);
}
}오른쪽 트리로 갈 때 i값을 빼주는 것에 주의해야 할 듯 하다.
[백준 - 1280] 나무 심기
문제: https://www.acmicpc.net/problem/1280
심는 위치를 x라고 할 때 x기준으로 왼쪽에 있는 나무들과 오른쪽에 있는 나무들의 거리를 따로 계산해야한다.
왼쪽에 나무가 n개가 있고 각각 위치를 a1, a2,...,an 이라고하면 x와 나무들의 거리는 다음과 같이 된다.
(x-a1) +(x-a2) +...+(x-an) = nx -sum(a)
따라서 심는곳의 왼쪽에 있는 나무의 갯수와 위치의 총합 을 알아야 한다.
이 두 정보는 세그먼트 트리로 얻으면 된다.
오른쪽도 비슷하게 처리하면 끝.
[백준 - 17371] 이사
문제: https://www.acmicpc.net/problem/17371

빨간 점이 최적의 위치이고, 가장 가까운 곳까지의 거리가 x 일 때
집 위치를 최적의 위치에서 가장 가까운 곳으로 옮긴다면 가장 가까운 곳까지의 거리는 x 만큼 줄어든다.
반면 가장 먼 곳까지의 거리는 아무리 많이 늘어나봐야 x만큼 늘어난다.
이동하면서 가장 먼 곳의 점의 위치가 바뀌어도 마찬가지다.
따라서 최단거리가 0인 지점에서 최적해가 항상 존재한다.
각 점에서 다른 점까지의 거리의 최댓값을 계산하여 적당히 답을 도출하면 된다.
이 발상을 하기가 쉽지 않았는데, 난이도가 좀 스포일러가 된 것 같다.
[백준 - 3830] 교수님은 기다리지 않는다
문제: https://www.acmicpc.net/problem/3830
얼마전에 느리게 갱신되는 세그먼트 트리를 배워서 그것과 비교한 느낌으로 유니온 파인드를 구현해서 풀었다.
두 그룹을 합치는 경우를 그림으로 설명하겠다.
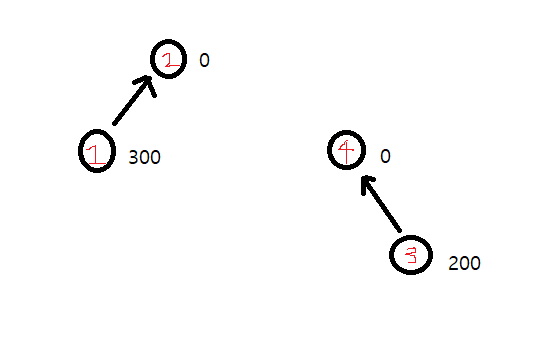
현재 무게는 1번: 300, 3번: 200으로 기록되어있다.
이 상태에서 ! 1 3 400, 즉 3번이 1번보다 400만큼 더 무겁다는 쿼리를 받았다 하자.
그렇다면 3번은 300+400=700이 되어야 한다.
3번이 속한 그룹 모두 +500만큼 조정을 해야되는 상황이다.
이 때 3번이 속한 그룹의 루트(4번)에 lazy와 value에 +500을 해준다.
그 후 4번을 1번이 속한 그룹의 루트(2번)에 연결해준다.
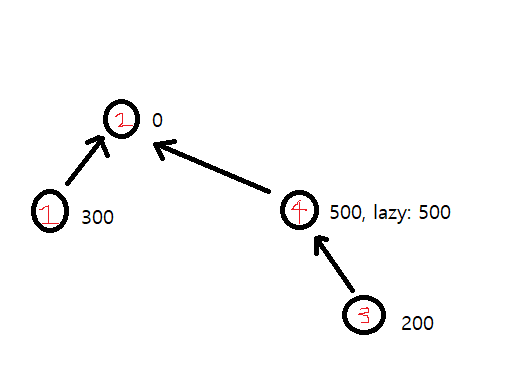
아직 4번 아래의 노드들은 직접적인 업데이트가 되지 않았다.
이 노드들은 find 를 할 때 만나는 부모들의 lazy 만큼 value를 업데이트 해주면 된다.
find를 한 경로에 있는 모든 노드들은 재귀적으로 value가 업데이트 되고 부모도 루트노드를 가르키게 최적화를 한다.
이 때 value와 함께 lazy도 업데이트를 해줘야 한다는 것에 주의해야한다.
예를들어 3번을 find 해서 value만 업데이트 한다면, 3번의 자식들은 lazy를 못받게 되는 상황이 발생한다.
ll parent[100001], lazy[100001],value[100001];
pll find(ll node, ll laz) //parent, lazy
{
if(node == parent[node])
return {node,laz};
ll curLazy = laz + lazy[node];
pll result = find(parent[node], curLazy);
value[node]+=result.second - curLazy;
lazy[node] += result.second - curLazy;
parent[node] = result.first;
return result;
}
void Union(ll u, ll v, ll w) // ! u v w
{
ll nu = find(u,0).first;
ll nv = find(v,0).first;
if(nu == nv) return;
ll gap = value[v] - value[u];
value[nv] += w- gap;
lazy[nv] += w- gap;
parent[nv] = nu;
}