1. 통계적 추론
1-1. 추론과 예측, 그리고 가정
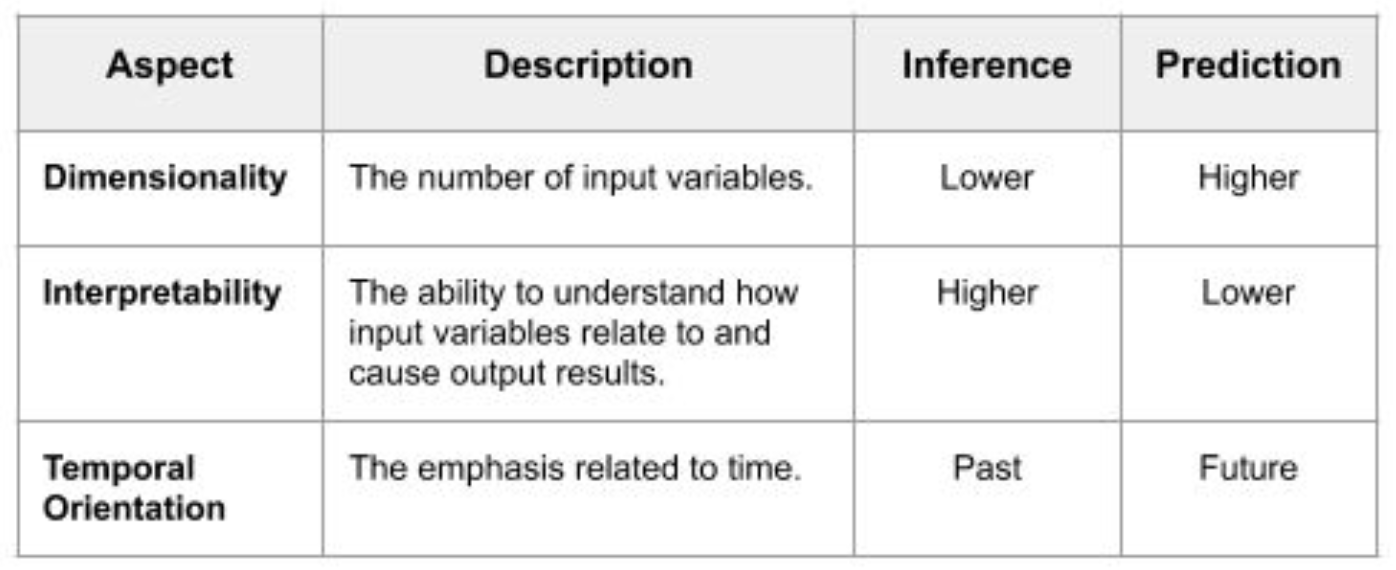
추론(inference)
- 변수들 사이의 관계를 이해하기 위함.
- 통계가 많이 사용됨
- 예측 성능이 상대적으로 떨어짐
예측(prediction)
- 예측 성능이 중요함
- ML/DL이 많이 사용
- 내부 구조에 대한 이해 어렵
통계적 가정 examples
- 잔차에 특정한 패턴이 없다는 가정
- 어떠한 분포를 따른다는 가정
- 검정하려는 특성(ex: 평균) 외에 다른 특성이 비슷하다는 가정 (ex: 분산)
평균 비교(two sample t-test)가정 examples
- 아웃라이어가 없음.
- 두 집단의 분산이 비슷함.
- 순서의 영향이 없음.
- 집단 내 각 관측치는 같은 분포.
통계적 가정의 의미?
- 가정이 맞지 않을 경우, 결과를 신뢰할 수 없음.
- 항상, 모든 통계적 가정이 맞다고는 확신할 순 없음.
- 검사한 것들에서 문제가 나오지 않았다 - 이제 그만 씨부리세요 할 수 있음.
- ML 모델 중 다수는 가정이 아예 없기도 함.
- 가정이 강력할수록 그 결과에 대해 정확한 추론이 가능.
- But, ML에서도 통계적 가정을 활용하여 성능 올리기가 가능하긴함.
1-2. 모수와 추정
모수 parameter란?
- 각 분포의 특성을 결정짓는 수
- ex) 정규분포의 평균, 분산
- 통계적 추론의 대부분은 모수를 추정하는 것
- 모수에 대한 추정량 estimator는 확률변수로, 어떠한 분포를 따를 수 있음.
모수 추정 examples
- t-test: 각 그룹의 평균 추정(t분포)
- ANOVA: 각 그룹의 평균 및 분산 추정(그룹 내 분산과 그룹 간 분산에 대한 비교: F분포)
- Linear Regression: Y=aX+b+e에서 a,b에 대한 추정(t분포)
- K-means: 각 집단의 평균과 분산을 추정(Normal 분포)
2. 추론의 이해

2-1. 추론 도구: 추정량
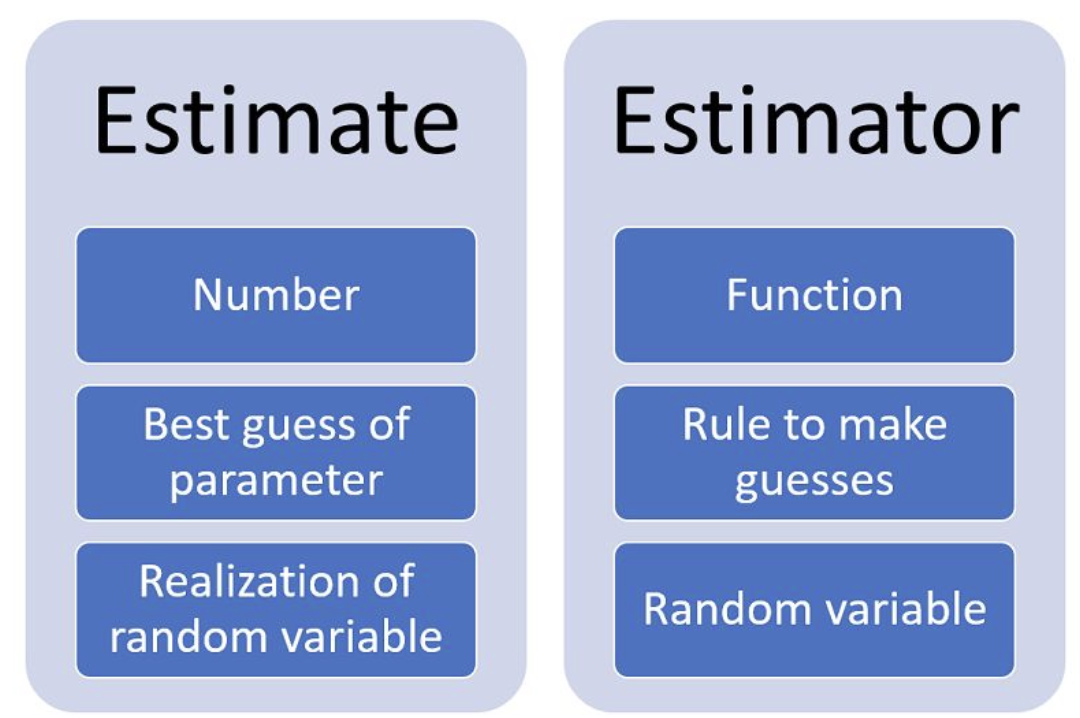
추정량 Estimator
- 추정하려는 모수에 대한 예측
- 확률 변수들로부터 만들어내는 통계량, 그 자신도 확률변수
- ex) 정규분포의 평균을 추정할 때, 각 확률 변수의 산술평균을 추정량으로 함
- 실제 데이터로부터 만든 값은 추정치 Estimate
- 일반적으로 모수 Θ에 대한 추정량은, Θ^으로 표기
- ex) 평균 μ에 대한 추정량은 μ^으로 표기. μ^ = sum(Xi) / n
좋은 추정량의 성질?
- Unbiased: E(Θ^) = Θ
- Efficient: Low variance (좀 더 복잡하니 패스)
- Consistency: n이 무한히 커질 때 Θ^가 Θ로 수렴 (극한)
편향 bias - 분산 variance
(loss는 model의 예측과 실제 값 간의 차이를 측정하는 metric, bias는 모델의 정확성과 일반화 능력을 나타내는 개념. 헷갈리지 말자)
- 예측과 실제값 사이의 오차는, 이론적으로 편향Bias와 분산Variance으로 쪼개질 수 있음
- 둘 중 무엇을 얼마냐 줄이냐가 모델에 따라 다를 수 있음
- ex) LASSO는 약간의 편향을 내주지만 분산을 줄임으로써 더 적은 오차를 달성하는 모델
<편향 (Bias)>:
편향은 모델이 학습 데이터에 대해 너무 단순화된 가정을 하는 경향
높은 편향을 가진 모델은 학습 데이터의 중요한 패턴이나 관계를 잘 포착하지 못하고, 이로 인해 학습 데이터와 테스트 데이터 모두에서 성능이 떨어질 수 있음.
예를 들어, 선형 회귀는 비선형 관계를 갖는 데이터에 대해 높은 편향을 가질 수 있음.
<분산 (Variance)>:
분산은 모델이 학습 데이터의 임의의 변동성에 너무 민감하게 반응하는 경향을 나타냄.
높은 분산을 가진 모델은 학습 데이터에 과적합(overfitting) 되어, 새로운 데이터에 대한 예측이 일관성이 없거나 불안정.
예를 들어, 복잡한 결정 트리나 딥 러닝 모델은 높은 분산을 가질 수 있음.
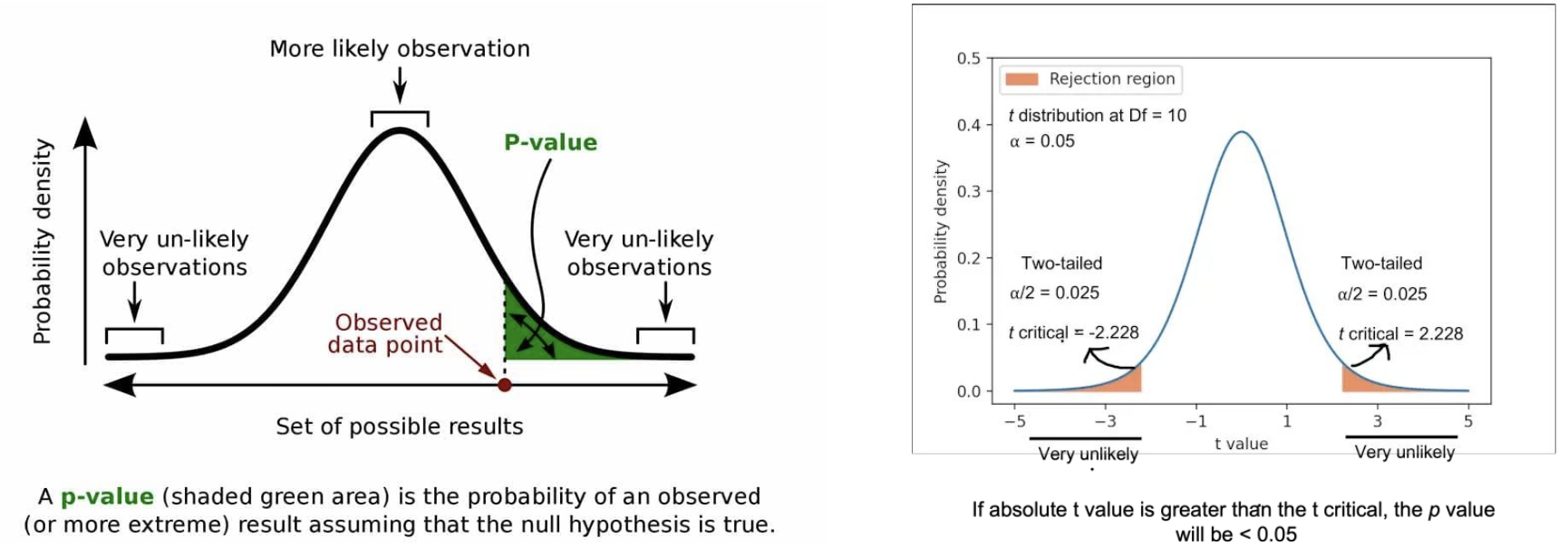
p-value
-
귀무 가설이 맞다고 가정했을 때 데이터가 얼마나 극단적인지를 나타내는 값
-
p-value 0.05이하이면 귀무가설 기각
2-2. 추론의 방법론
MLE(Maximum Likelihood Estimator)
가능도 함수 Likelihood function(a.k.a 우도함수)
- 주어진 모수에 대해 관측된 데이터가 나올 확률
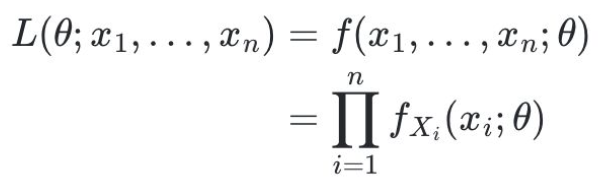
- 목표: 가능도를 최대로하는 theta를 찾는 것
몬테카를로 MonteCarlo
- 시뮬레이션을 많이 돌리는 것
- 동전을 직접 던져 앞면이 나올 확률을 구하는 것도 개념적으로는 몬테카를로
- 당연히 컴퓨터 사용하는 게 일반적
- ex) -1 ~ 1 사이의 값을 두 개 뽑아(x, y) 반지름 1인 안에 들어가는지 검사함으로써 원의 부피를 근사
부트스트랩 Bootstrap이란?
- 재추출을 반복하여 신뢰구간까지 구할 수 있는 MC 기법(resampling)
- 실제 ML에서도 많이 쓰임
- 연산량이 많다는 단점이 있지만, 어디서나 쓰일 수 있다는 장점
<목적>
신뢰구간 추정, 가설 검정, 회귀분석 시 이용
<수행과정>
1. 재표본 추출: 원본 데이터에서 복원 추출(중복 허용)을 사용하여 재표본을 생성. 재표본은 원본 데이터 크기와 동일하게 생성
2. 통계량 계산: 각 재표본에 대해 원하는 통계량(예: 평균, 중앙값, 분산)을 계산
3. 분포 추정: 여러 번의 재표본 추출을 통해 얻은 통계량을 히스토그램 또는 밀도 함수를 사용하여 분포로 나타냄
4. 신뢰구간 추정 또는 가설 검정: 추정된 분포를 사용하여 신뢰구간을 계산하거나 가설 검정을 수행
부트스트랩은 표본 크기가 작거나 모집단 분포에 대한 가정이 만족되지 않을 때 유용하며, 통계 추정의 불확실성을 평가하는 데 도움을 줌
3. 통계적 가설 검정
3-1. 통계적 가설Statistical Hypothesis이란?
- 주어진 자료가 특정 가설을 충분히 뒷받침하는지 여부를 결정하는 통계적 추론 방법
- ex)
- 지난 달 한 달 간, 어머니와 아버지 두 분에 대한 각각의 전화횟수와 평균 시간은 어땠나요?
- 지난 1년간 명절이나 생신 때 드리는 용돈/선물의 금액의 합은 어떤가요?
- 평소 애정 표현의 횟수를 정확히 측정할 수 있을까요?
3-2. T-test deep dive
t- 분포
모분산을 모를 때 모평균을 구하는 것(표본의 크기가 30이하, 모분산을 몰라야함)
t- test
"두 모집단 간의 모평균은 차이가 없다" - 귀무가설(p-value 0.05 이상 일때 기각)
"두 모집단 간의 모평균은 차이가 있다" - 대립가설(p-value 0.05 이하 일때 채택)
독립표본 t test
서로 독립인 두 집단 비교
예시 : 수도권과 지방의 집 값
대응표본 t test
동일 그룹에 어떤 처리 후 전후 비교
예시 : 대출 규제 시작 전과 후의 집 값
순서
if 표본의 크기가 10~30이면, -> 정규성 검정
- 정규성이라면, 등분산 검정
- 정규성이 아니라면, 순위합 검정
if 표본의 크기가 30 이상이면, -> 등분산 검정
- 등분산이라면, 등분산 가정 독립표본 t test
- 등분산이 아니라면, 이분산 가정 독립표본 t test
독립표본 t-test: 수도권과 지방 집값 비교 / github link
t-test의 한계
- 3개 이상의 집단에 대한 검정이 불가능
- A, B, C 집단에 대해 검정한다면..?
○ 대안: A&B, A&C, B&C 이렇게 세 번한다면 ..? ○ 각 시행이 오류가능성을 안고있음.
○ 95% 확률 뽑기를 3번 연속 통과하려면, (0.95)^3 = 0.86 -> 본 페르니 방법
○ 하지만 집단의 수가 늘어날수록 기하급수적으로 오류의 가능성이 늘어남
● 이에 대한 솔루션: ANOVA
