그리디(Greedy) 알고리즘
그리디 알고리즘은 말 그대로 탐욕스러운 알고리즘입니다.
그리디 알고리즘의 핵심은 "현재의 선택지 중에 최고만을 선택하자" 입니다.
탐욕스러운 사람은 미래를 생각하지 않고 현재의 이득만을 챙기는 것과 같이, 그리디 알고리즘은 미래의 선택지는 고려하지 않습니다.
즉, 그리디 알고리즘은 모든 경우에 대해 최적의 결과를 보장하지는 않습니다.
그리디 알고리즘 예시1
슬픈 통학생
A가 있습니다.
A는집에서학교까지 통학을 하려고 합니다.
슬프게도집에서학교까지 한번에 가는 교통수단이 없습니다.
이 때,A가학교에 가장 빠르게 갈 수 있는 방법을 구하세요.
이런 문제의 경우 그리디 알고리즘을 사용할 수 있습니다.
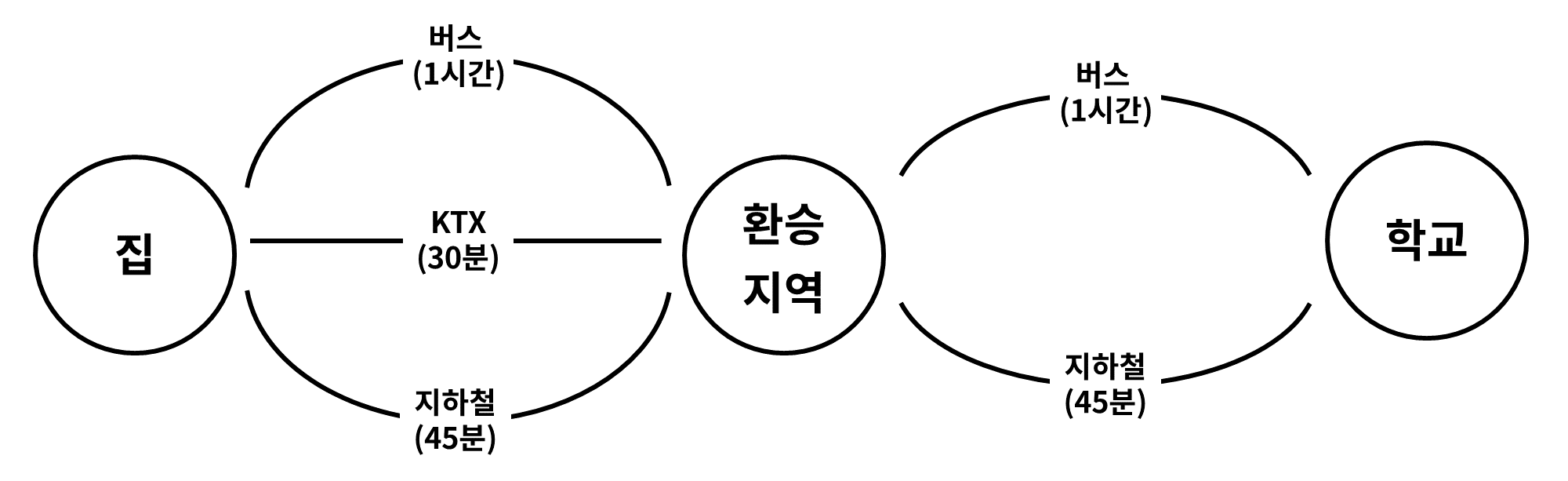
문제의 해결 과정은 다음과 같습니다.
-
집에서환승 지역까지 가는 상황에서의 최적의 선택KTX를 선택합니다. -
횐승 지역에서학교까지 가는 상황에서의 최적의 선택지하철을 선택합니다. -
이전의 선택들을 합한 1시간 15분이 학교까지 가장 빠르게 갈 수 있는 방법입니다.
이 문제의 예시 처럼 이전 선택의 결과가 이후 선택의 결과에 영향을 미치지 않는 경우에 그리디 알고리즘을 사용할 수 있습니다.
하지만, 아래의 경우처럼 이전 선택의 결과가 이후 선택의 결과에 영향을 미치는 경우에는 그리디 알고리즘을 사용할 수 없습니다.
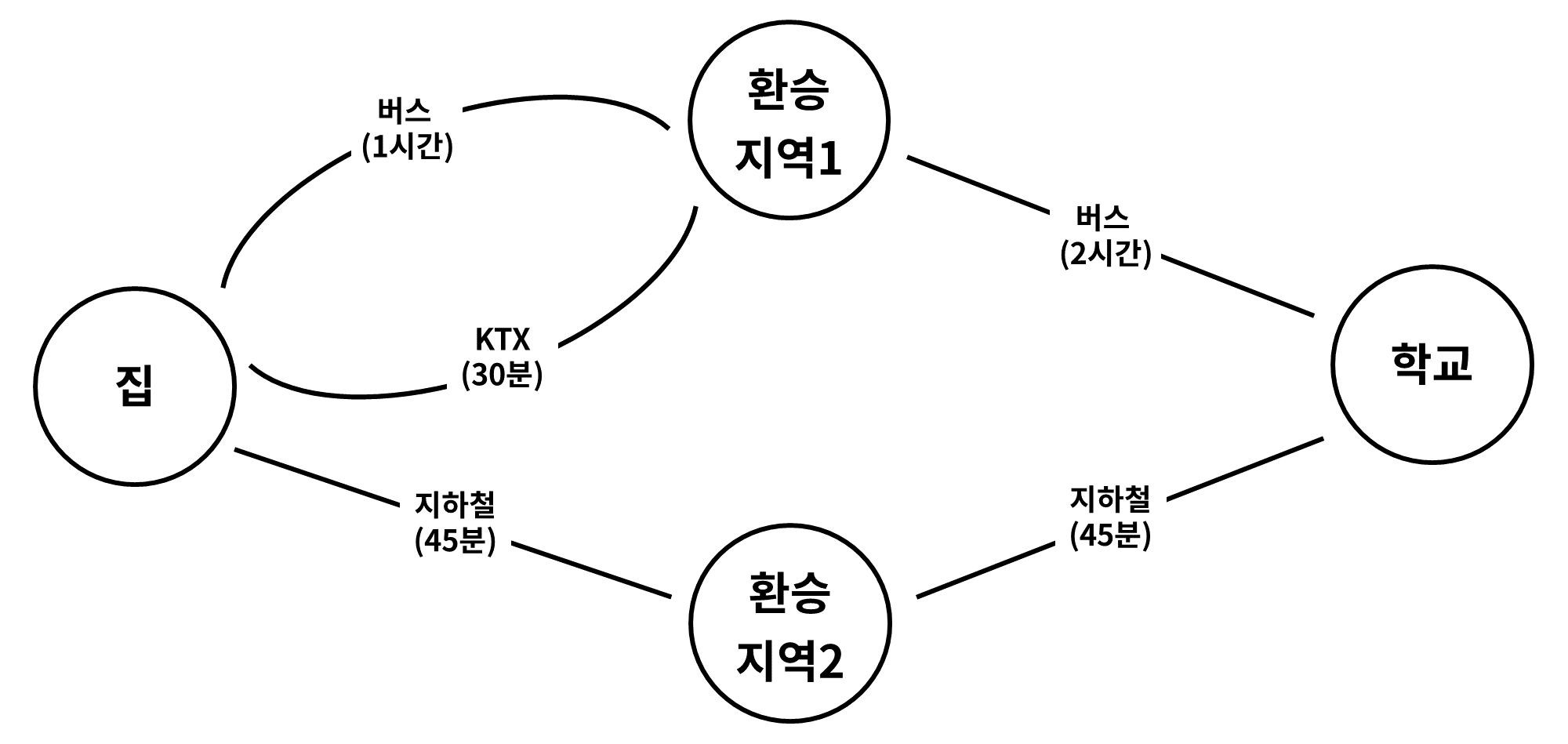
이 경우에는 그리디 알고리즘을 사용하게 되었을 때, 집에서 KTX를 타고 환승 지역1에 가고 환승 지역1에서 학교까지 버스를 타고 가게 되어 2시간 30분이 나오게 됩니다.
하지만, 실제 정답은 집에서 환승 지역2까지 지하철을 타고, 환승 지역2에서 학교까지 지하철을 타고 가는 1시간 30분이 되게 됩니다.
그리디 알고리즘 예시2
A는 마트에서 계산원으로 일하고 있습니다.
A는 손님에게 거스름돈을 줄 때 최대한 적은 개수의 화폐로 거스름돈을 주고 싶습니다.
거스름돈의 금액이 주어질 때, 필요한 화폐의 개수의 최소값을 구하세요.
단, 계산대에는 충분히 많은50,000원,10,000원,5,000원,1,000원,500원,100원,50원,10원이 있고, 거스름돈을 줄 수 없는 경우는 주어지지 않습니다.
이런 거스름돈 문제의 경우에도 그리디 알고리즘을 사용할 수 있습니다.
큰 단위의 돈부터 순서대로 남은 거스름돈의 최대 만큼 선택하는 과정을 통해 문제를 해결할 수 있습니다.
거스름돈이 114,320원인 경우 문제의 해결과정은 다음과 같습니다.
-
114,320원에 대해 5만원권을 최대로 꺼냅니다. (2장 - 10만원)
-
남은 14,320원에 대해 1만원권을 최대로 꺼냅니다. (1장 - 1만원)
-
남은 4,320원이 5천원보다 작기 때문에 5천원권은 꺼낼 수 없습니다.
-
남은 4,320원에 대해 1천원권을 최대로 꺼냅니다. (4장 - 4천원)
-
남은 320원에 대해 100원 동전을 최대로 꺼냅니다. (3개 - 300원)
-
남은 20원이 50원보다 작기 때문에 50원 동전은 꺼낼 수 없습니다.
-
남은 20원에 대래 10원 동전을 최대로 꺼냅니다. (2개 - 20원)
-
이전 단계의 합인 12개가 답이 됩니다.
만일, 화폐가 100원, 700원, 1000원과 같이 서로 배수 관계가 아닌 경우에는 이전 선택이 이후 선택에 영향을 미치게 되므로 그리디 알고리즘을 사용할 수 없습니다.
위의 경우로 1400원을 거슬러 준다면, 그리디 알고리즘을 사용하면 1000원 1개, 100원 4개가 답으로 나오지만, 실제 정답은 700원 2개가 됩니다.
결론
그리디 알고리즘은 현재의 선택이 다음 선택에 영향이 가지 않는 경우 사용할 수 있는 알고리즘입니다.
따라서, 어떤 문제에 대해 그리디 알고리즘을 사용할 때는 현재의 최적의 선택들을 합이 전체의 경우에서 최적의 선택인지를 잘 파악하고 사용하는 것이 중요합니다.