그래프 표현 방식

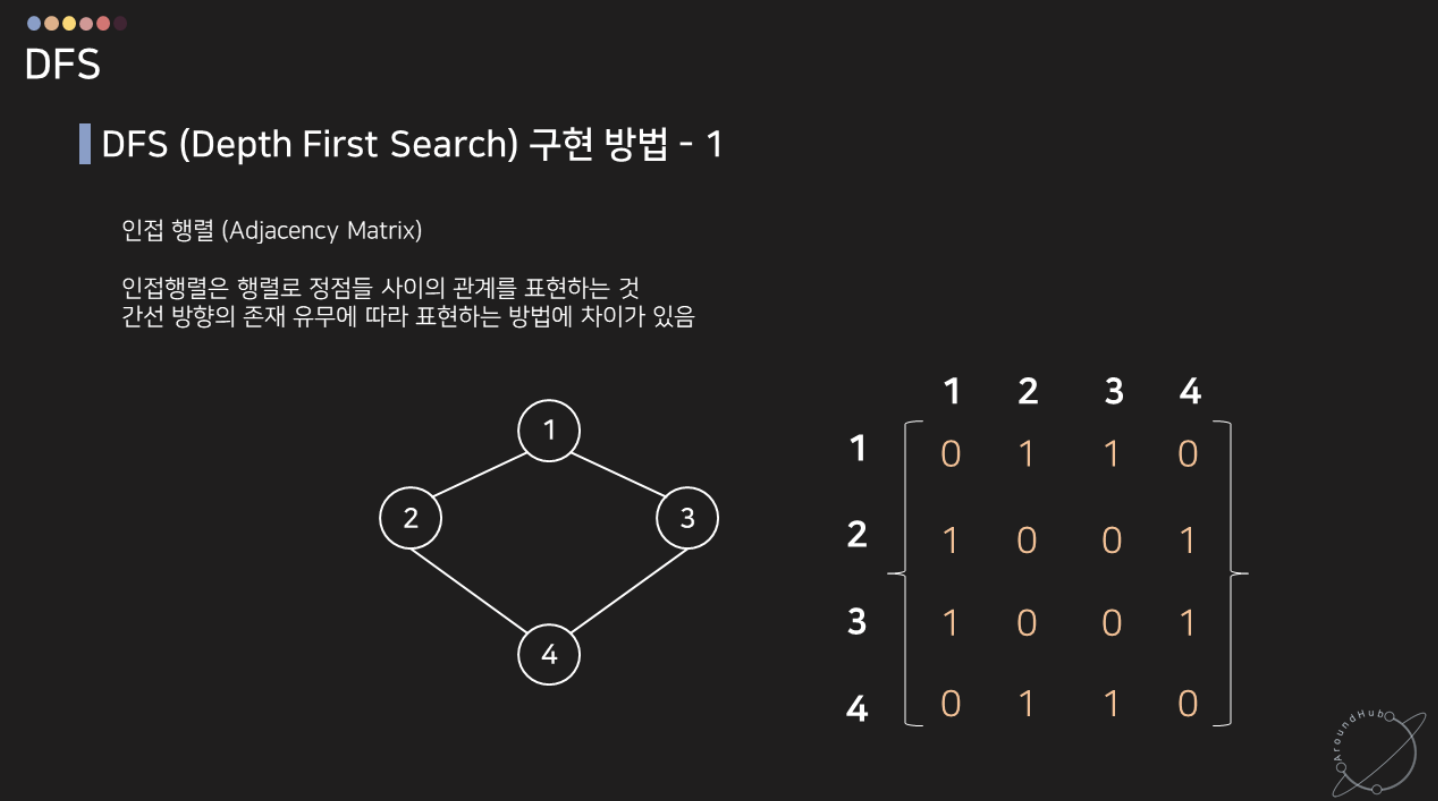
1. 인접 행렬

• 2차원 배열을 이용해 그래프를 표현
• 행 번호는 노드의 번호를 의미, 열 번호는 노드와 연결된 노드들에 대한 정보를 의미
• 열결되어 있으면 1, 연결되어 있지 않으면 0으로 표현

장점

• 구현이 쉽다.
• 연결 여부를 확인하기 용이하다.

단점

• 노드와 연결된 모든 노드들에 방문해보고 싶을 때 행렬의 모든 인덱스를 0인지 1인지 확인해야 하므로 시간 복잡도가 크다.

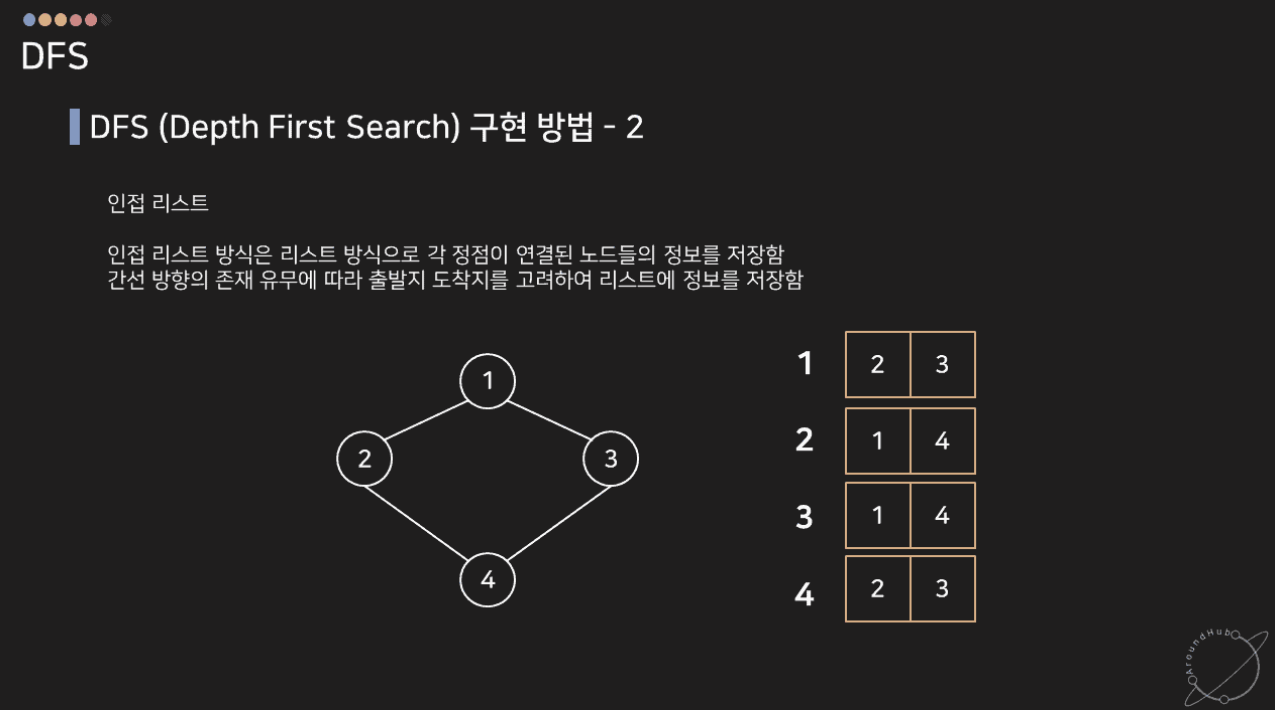
2. 인접 리스트

• 연결 리스트를 이용하여 그래프를 구현
• array[i]가 노드 i에 연결된 노드들을 원소로 갖는 리스트를 의미. array[i]는 그래프의 원소.

DFS(깊이 우선 탐색)

• 그래프 전체를 탐색하는 방법 중 하나
• 시작 노드에서 다음 분기로 넘어가기 전에 해당 분기에 대한 탐색을 완료하고 넘어가는 방법
• 재귀함수나 스택으로 구현

Logic

1. 시작 노드를 스택에 삽입하고 방문처리
2. 스택의 최상단의 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다
3. 2번 과정을 반복

• 노드를 방문할 때 방문여부를 표시해주어야 한다.
  
  
  

장점

• 로직에서 하나의 경로만을 기억하므로 저장공간의 수요가 비교적 적다.
• 찾으려고 하는 노드가 깊은 단계에 있는 경우 빨리 구할 수 있다.

단점

• 해가 없는 경로에 깊이 빠질 가능성이 있다.
• 얻어진 해가 최단 경로가 아닐 수 있다.(목표에 이르는 경로가 다수인 경우 DFS는 해에 다다르면 탐색을 종료하므로 항상 최적인 경로를 찾을 수는 없다.)
• 해가 없는 경로가 깊을 경우 탐색시간이 오래 걸릴 수 있다.

BFS(너비 우선 탐색)

• 시작 노드를 방문한 후 시작 노드에 있는 인접한 모든 노드들을 우선 탐색하는 방법(그래프에서 가장 가까운 노드부터 우선적으로 탐색)
• 큐를 사용하여 구현(재귀함수로는 구현할 수 없다.)
• 최단 경로 알고리즘을 계산할 때 사용

Logic

1. 탐색 시작 노드를 큐에 삽입하고 방문 처리
2. 큐에서 노드를 꺼낸 뒤에 해당 노드의 인접 노드 중 방문하지 않은 노드를 모두 큐에 삽입 후 방문 처리
3. 2번 과정을 반복
   

장점

• 출발노드에서 목표노드까지의 최단 경로를 찾을 수 있다.

단점

• 경로가 긴 경우에는 탐색을 하는데 사용되는 가지가 급격하게 많아지므로 많은 기억 공간을 필요로 한다.