양자 컴퓨팅 기초

양자 컴퓨팅이란 무엇인가요?

양자 컴퓨팅이란 양자역학적인 현상을 이용하여 자료를 처리하는 것을 말합니다. 일반적인 컴퓨터에서 우리는 비트(bit)를 이용하여 자료를 처리하지만 양자 컴퓨터에서는 큐비트(Qubit)라는 단위를 이용합니다. 최근에는 양자 컴퓨터를 이용한 양자 딥러닝에 대한 연구가 진행되고 있습니다.

이어질 글에서는 양자 딥러닝을 이해하기에 앞서 양자 컴퓨팅에 대한 이해를 돕기 위해 큐비트, 양자 컴퓨팅을 위한 선형대수, 그리고 게이트에 대해 설명하고자 합니다.

큐비트

"이미지 출처: 김중헌 교수님 유튜브"

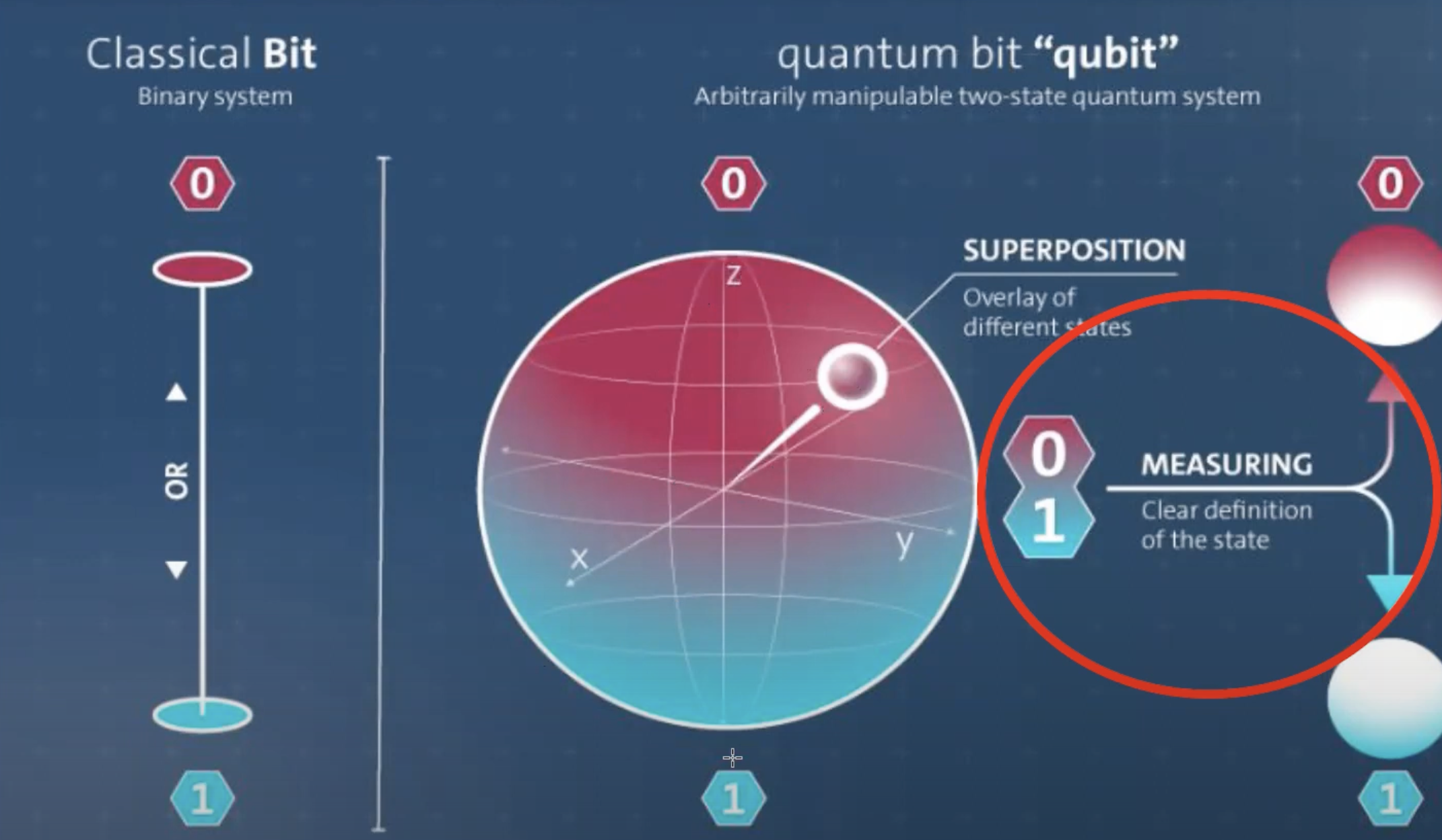
일반적으로 우리가 사용하는 비트는 0 또는 1의 값을 베타적으로 가지지만 큐비트에서는 다릅니다. 큐비트는 구의 확률값으로서 값이 존재합니다. 이해를 돕기 위해 가장 많이 쓰이는 슈뢰딩거 고양이 사고실험에 비유해 보겠습니다. 슈뢰딩거의 고양이 사고실험에서는 상자 속의 고양이가 살아있으면서 죽어있을수 있고 상자를 열어 확인 하였을 때 우리는 그 결과를 알 수 있습니다. 이와 마찬가지입니다. 조금 더 전문적인 용어를 이용하여 큐비트를 설명해보겠습니다.

관측 전의 여러 값을 가질 수 있는 상태를 중첩된 상태인 superposition 이라고 합니다. 관측인 measuring이 일어난 후에는 하나의 상태로 고정됩니다.

이제 큐비트를 수식으로 표현해보겠습니다.

$\alpha$와 $\beta$는 각각 0을 발견할 확률과 1을 발견하기 위한 확률을 표현하는 복소수입니다. 확률값 그 자체는 아닙니다.
위 값이 0이 될 확률은 $| \alpha|^2$, 1이 될 확률은 $| \beta|^2$입니다. 복소수의 제곱은 해당 복소수와 복소수의 켤례 복소수의 곱을 통해 계산할 수 있습니다. 아마 고등학교 1학년 수2 시간에 배운 거 같은데 잘 기억이 나질 않으니 복습하는 시간을 갖도록 하겠습니다.

위 방법을 이용하여 아래 큐비트의 확률값들을 구해보겠습니다.

0이 될 확률은 $\frac{2}{3}$, 1이 될 확률은 $\frac{1}{3}$인 것을 알 수 있습니다.

양자 컴퓨팅을 위한 선형대수

복소수 선형 공간 $C^n$: 복소수 n개 쌍으로 구성되는 벡터공간으로, 아래 예시에서는 $n=2$ 입니다.
큐비트의 $|{\Psi}\rangle = \alpha|{0}\rangle + \beta|{1}\rangle$ 표현을 벡터를 이용하여 아래와 같이 대체할 수도 있습니다.

또한 선형대수학 시간에 배운 선형 독립과 생성 집합의 유일성을 이용하여 다른 큐비트들을 표현하는 것도 가능합니다.

이번에는 내적에 대해 알아보겠습니다. 유클리드 공간에서의 내적은 실수 도메인에서 이루어집니다. 하지만 복소수 선형 공간에서의 내적은 복소수 도메인에서 이루어집니다.

$\langle{a|b}\rangle$는 $|{a}\rangle$와 $|{b}\rangle$의 내적
$\langle{a|b}\rangle=0$이면 두 벡터가 직교
$\langle{a|b}\rangle^* = \langle{b|a}\rangle$
$||u|| = \sqrt{\langle{u|u}\rangle}$: 벡터의 길이
$\langle{u|u}\rangle \geq 0$: 등호가 성립하려면 $|{u}\rangle > 0$

두 벡터의 내적을 구하려면 한 벡터의 Hermitial 켤례벡터를 구해야합니다.
$(|{u}\rangle)^+ = \langle{u}|$

$C^3$에 속한 두 벡터 $|{a}\rangle = \left( \begin{array}{cc} -2 \\ 4i \\ 1 \end{array} \right)$, $|{b}\rangle = \left( \begin{array}{cc} 1 \\ 0 \\ i \end{array} \right)$가 있을 때,
$\langle{a|b}\rangle = ((|{a}\rangle)^T)^* (|{b}\rangle) = (-2\ -4i\ 1)$ $\left( \begin{array}{cc} 1 \\ 0 \\ i \end{array} \right) = -2 + i$ 가 됩니다.

게이트

위의 연산을 응용하면 양자 컴퓨팅에 쓰이는 게이트 연산이 됩니다. 아직까지 이것들을 이용하여 어떻게 양자 딥러닝을 구성하는지 이해하기 어렵습니다. 우선 딥러닝의 개념을 다시 생각해보겠습니다. 딥러닝을 이용하면 우리가 원하는 하는 함수의 근사를 얻고자 하는 것입니다. 이를 위한 선형과 비선형 관계들을 표현하기 위한 연산들의 연속입니다. 양자 딥러닝에서도 마찬가지입니다. 선형 관계를 표현하기 위한 게이트와 비선형 관계를 표현하기 위한 게이트가 있습니다.

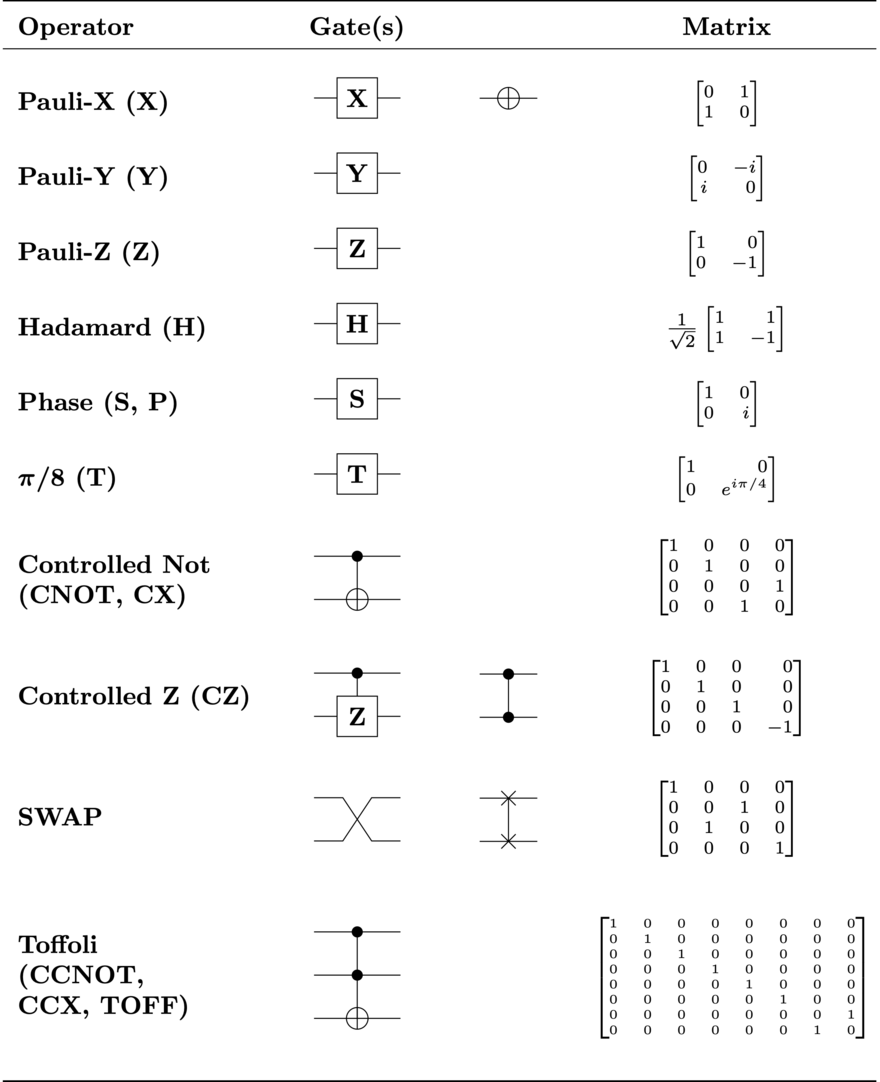
"이미지 출처: 위키디피아"

선형 관계의 표현은 큐비트를 구성하는 구의 회전을 일으키는 Rotation Gate에 의해 이루어집니다. 그리고 비선형 관계의 표현은 CNOT Gate나 Toffoli Gate처럼 그들간의 wiring(연결)에 의해 이루어집니다. 이러한 게이트들을 이용하면 양자 딥러닝을 위한 Quantum Circuit을 만들 수 있습니다.

마치며

이 글에서 간단하게 양자 컴퓨팅이 무엇인지에 대해 알아보았습니다. 그래서 이것으로 어떻게 양자 딥러닝을 하며 무엇을 할 수 있는지에 대해 궁금하신 분들이 있을 것으로 예상합니다. 그리고 우리가 알기로 양자 컴퓨터는 절대온도에서 동작하는 것으로 아는데 우리가 이것을 직접 사용해보기에는 무리일 것으로 생각합니다.
이를 위해 우리가 사용하는 Tensorflow와 PyTorch에서는 양자 딥러닝을 시뮬레이션할 수 있는 라이브러리를 제공하고 있습니다. 아직 단순한 계산밖에 이용해 볼 수 없지만 관심이 있으신 분들은 아래 링크를 참조하시면 좋을 거 같습니다. 직접 실습해 볼 수 있는 프로젝트들도 준비되어 있습니다.

고려대 김중헌 교수님 강의
Tensorflow Quantum 머신러닝
torchquantum

저 또한 양자 강화학습에 관심이 있어 공부 중에 있습니다. 간단하게 binary decision을 하는 장치가 10개 있다고 가정해봅시다. 그렇다면 action space는 $2^{10}$이 됩니다. action space가 기하급수적으로 늘어나는 상황에서는 log scale로 차원을 줄일 수 있다고 알려진 양자 강화학습이 도움이 될 것입니다.

긴 글을 읽어주셔서 감사합니다.

작성자 : 3기 장인성