💡 BFS
Breath First Search : 다차원 배열을 탐색할 때, 너비를 우선으로 탐색하는 알고리즘
-
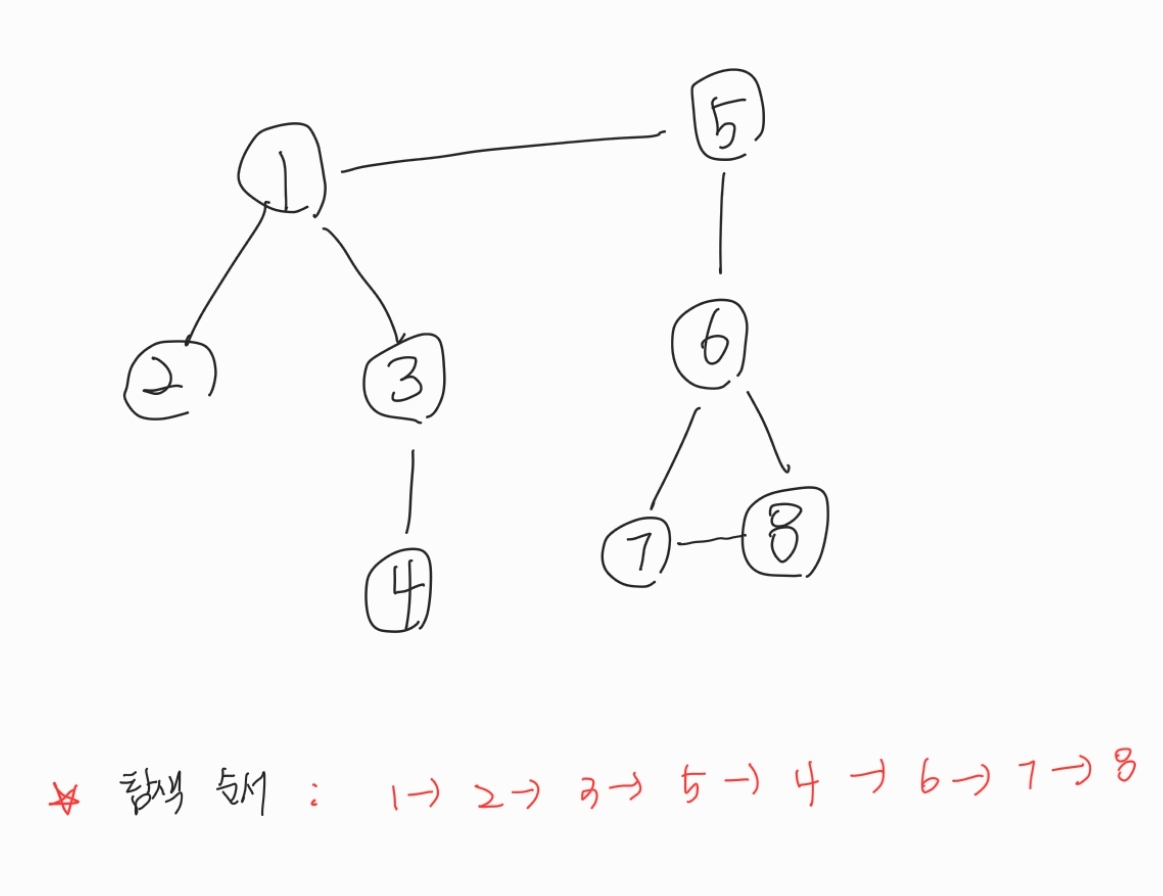
int[][] graph: 그래프를 2차원 배열로 표현-
배열의 인덱스 : 노드 번호 (0번 노드는 없으므로 아무것도 입력하지 않음)
-
해당 인덱스 내의 요소 : 인접한 노드 번호
-
-
boolean[] isVisit: 노드의 방문 여부 표시 -
bfs(int start):start번 노드부터 탐색 수행- 큐에 시작점을 넣고 방문 표시
- 큐의 가장 앞에 위치한 노드를 꺼내고 인접한 노드 탐색
2-1. 인접한 노드에 방문 표시가 없다면 큐에 넣고 방문 표시 후 2번 반복
2-2. 인접한 노드가 없거나 이미 방문했다면 2번 반복 - 큐가 비면 탐색 종료
import java.util.*;
public class Main {
// 그래프 : 인덱스 - 인접 노드 형태
static int[][] graph = {{}, {2,3,5}, {1}, {1,4}, {3}, {1,6}, {7, 8}, {6,8}, {6,7}};
// 노드 방문 여부
static boolean[] isVisit = new boolean[graph.length];
// 탐색 순서 출력
static StringBuilder sb = new StringBuilder();
public static void main(String[] args) {
// 1번 노드부터 탐색 시작
bfs(1);
bw.write(sb + "");
bw.close();
}
static void bfs(int start) {
Queue<Integer> q = new LinkedList<>();
q.offer(start); // 1. 시작 노드 삽입
isVisit[start] = true; // 1. 시작 노드 방문 표시
while(!q.isEmpty()) { // 3. 큐가 빌 때까지 반복
int idx = q.poll(); // 2. 탐색할 노드 인덱스
sb.append(idx + " ");
for(int i=0;i< graph[idx].length;i++) { // 2. 인접한 노드 탐색
int tmp = graph[idx][i];
if(!isVisit[tmp]) { // 2-1. 인접한 노드에 방문하지 않은 경우
q.offer(tmp); // 2-1. 인접 노드 큐에 삽입
isVisit[tmp] = true; // 2-1. 인접 노드 방문 표시
}
}
}
}
} ✅ 모든 칸이 큐에 한 번씩 들어갔다 나오므로, N개의 칸에 대한 시간 복잡도는
✅ 모든 칸이 큐에 한 번씩 들어갔다 나오므로, N개의 칸에 대한 시간 복잡도는 O(N) → 한 칸 당 O(1)
🙇🏻♀️ 참고 : [Algorithm] BFS(Breadth-first search)를 Java로 구현해보자!
📒 연습문제
📝 예제 1
[1926] 그림 : 파란색으로 칠해진 칸들 중, 상하좌우로 연결된 모든 칸을 탐색하기 →
(0, 0)에서 시작
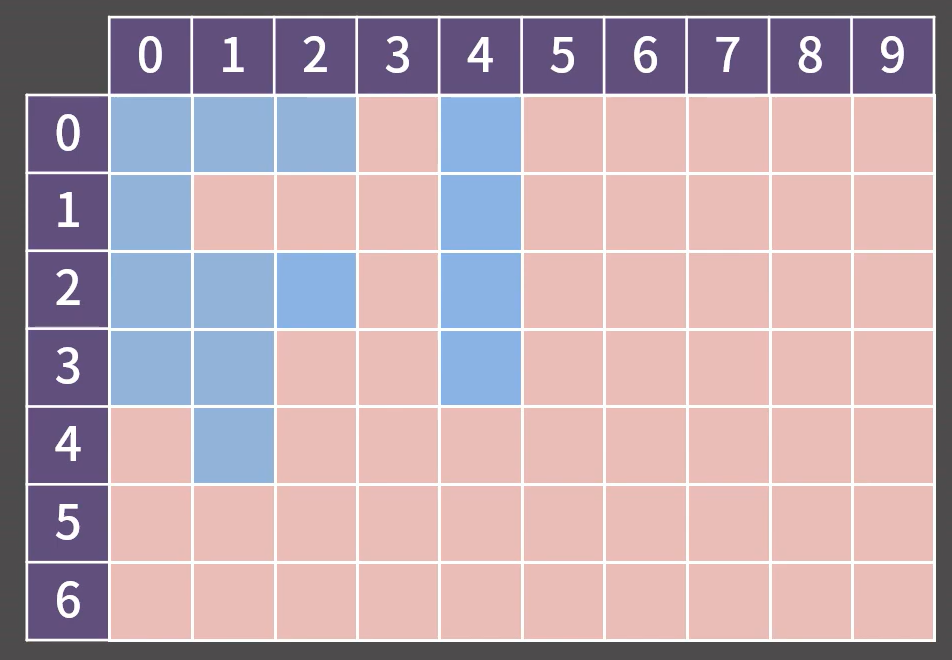
-
시작 지점인
(0, 0)에 대해 방문 표시하기 -
(0, 0)의 상하좌우를 탐색하여 파란색이면서 방문하지 않은 칸의 좌표를 큐에 삽입한 후 방문 표시하기
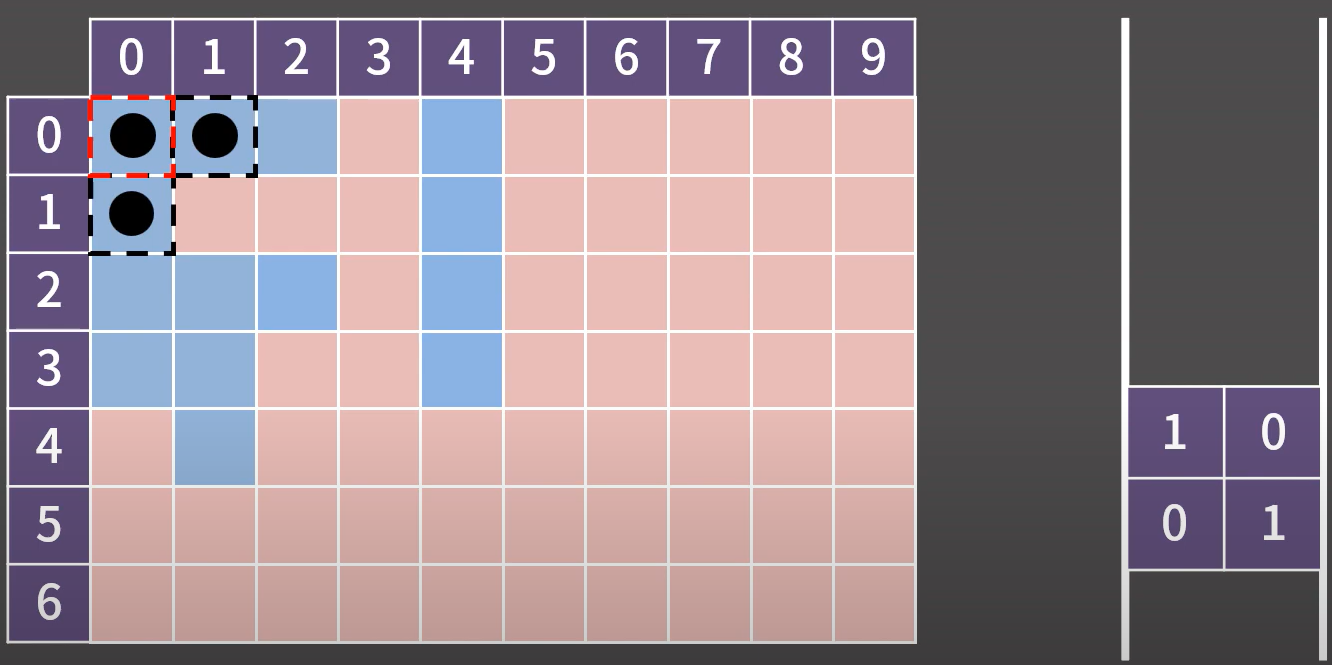
-
큐의 가장 앞 원소 좌표로 이동하며 큐에서 해당 좌표를 제거한 후, 1번 과정 반복
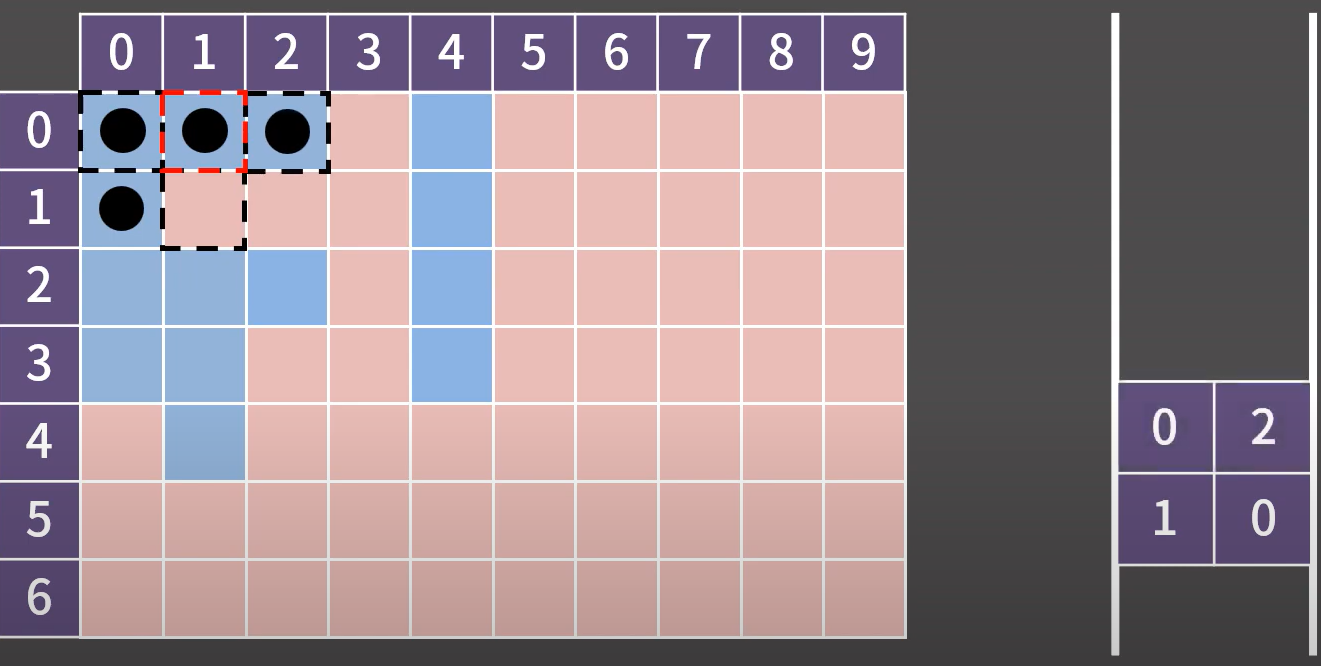
-
큐가 비면 탐색 종료
✔️ 구현
import java.io.*;
import java.util.*;
public class Main {
static int[][] graph;
static boolean[][] isVisit;
static int[] dx = {-1, 1, 0, 0};
static int[] dy = {0, 0, -1, 1};
static int n, m;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken()); // 세로 (행)
m = Integer.parseInt(st.nextToken()); // 가로 (열)
graph = new int[n][m];
isVisit = new boolean[n][m];
for(int i=0;i<n;i++) {
st = new StringTokenizer(br.readLine());
for(int j=0;j<m;j++) {
graph[i][j] = Integer.parseInt(st.nextToken());
}
}
int cnt = 0;
int max = 0;
for(int i=0;i<n;i++) {
for(int j=0;j<m;j++) {
if(graph[i][j] == 1 && !isVisit[i][j]) {
max = Math.max(max, bfs(j, i));
cnt++;
}
}
}
bw.write(cnt + "\n" + max);
bw.close();
}
static int bfs(int x, int y) {
Queue<int[]> q = new LinkedList<>();
q.offer(new int[] {x, y});
isVisit[y][x] = true;
int area = 1;
while(!q.isEmpty()) {
int[] tmp = q.poll();
int px = tmp[0]; int py = tmp[1];
for(int i=0;i<4;i++) {
int nx = px + dx[i];
int ny = py + dy[i];
if(nx < 0 || ny < 0 || nx > m-1 || ny > n-1) continue;
if(graph[ny][nx] == 1 && !isVisit[ny][nx]) {
q.offer(new int[] {nx, ny});
isVisit[ny][nx] = true;
area++;
}
}
}
return area;
}
}📝 예제 2 : 최단거리 측정
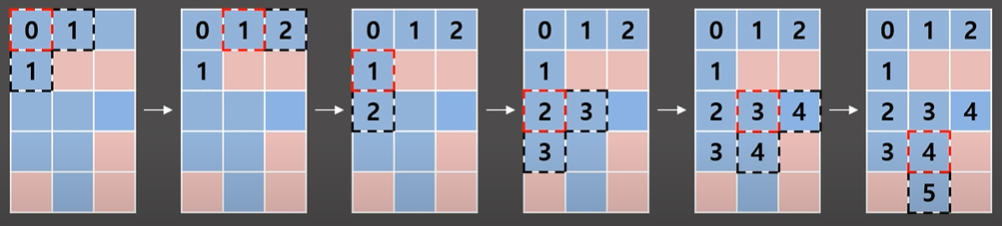
graph[x][y]: 이 칸으로 오기까지 거쳐온 칸의 수 =이전 칸의 값 + 1
import java.io.*;
import java.util.*;
public class Main {
static int[][] graph;
static boolean[][] isVisit;
static int[] dx = {-1, 1, 0, 0};
static int[] dy = {0, 0, -1, 1};
static int n, m;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
graph = new int[n][m];
isVisit = new boolean[n][m];
for(int i=0;i<n;i++) {
String s = br.readLine();
for(int j=0;j<m;j++) {
graph[i][j] = s.charAt(j) - '0';
}
}
bfs(0, 0);
bw.write(graph[n-1][m-1] + "");
bw.close();
}
static void bfs(int x, int y) {
Queue<int[]> q = new LinkedList<>();
q.offer(new int[] {x, y});
isVisit[x][y] = true;
while(!q.isEmpty()) {
int[] tmp = q.poll();
int px = tmp[0];
int py = tmp[1];
for(int i=0;i<4;i++) {
int nx = px + dx[i];
int ny = py + dy[i];
if(nx < 0 || ny < 0 || nx > n-1 || ny > m-1) continue;
if(graph[nx][ny] == 1 && !isVisit[nx][ny]) {
q.offer(new int[] {nx, ny});
isVisit[nx][ny] = true;
graph[nx][ny] = graph[px][py] + 1;
}
}
}
}
}📝 예제 3 : 시작점이 여러 개
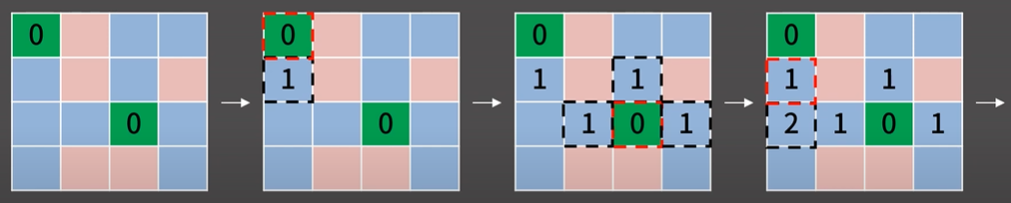
-
탐색 시작점이 여러 개인 경우
graph를 채울 때 시작점의 좌표를 큐에 넣고 시작하면 된다! -
시작점의 값이 1이므로, 최종 답은
graph[x][y] - 1
import java.io.*;
import java.util.*;
public class Main {
static int[][] graph;
static int[] dx = {-1, 1, 0, 0};
static int[] dy = {0, 0, -1, 1};
static int n, m;
static Queue<int[]> q = new LinkedList<>();
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
m = Integer.parseInt(st.nextToken());
n = Integer.parseInt(st.nextToken());
graph = new int[n][m];
for(int i=0;i<n;i++) {
st = new StringTokenizer(br.readLine());
for(int j=0;j<m;j++) {
graph[i][j] = Integer.parseInt(st.nextToken());
if(graph[i][j] == 1) q.offer(new int[] {i, j});
}
}
bw.write(bfs() + "");
bw.close();
}
static int bfs() {
while(!q.isEmpty()) {
int[] tmp = q.poll();
int px = tmp[0];
int py = tmp[1];
for(int i=0;i<4;i++) {
int nx = px + dx[i];
int ny = py + dy[i];
if(nx < 0 || ny < 0 || nx > n-1 || ny > m-1) continue;
if(graph[nx][ny] == 0) {
graph[nx][ny] = graph[px][py] + 1;
q.offer(new int[] {nx, ny});
}
}
}
int day = 0;
for(int i=0;i<n;i++) {
for(int j=0;j<m;j++) {
if(graph[i][j] == 0) return -1;
day = Math.max(day, graph[i][j]);
}
}
return day - 1;
}
}📝 예제 4 : 시작점이 두 종류
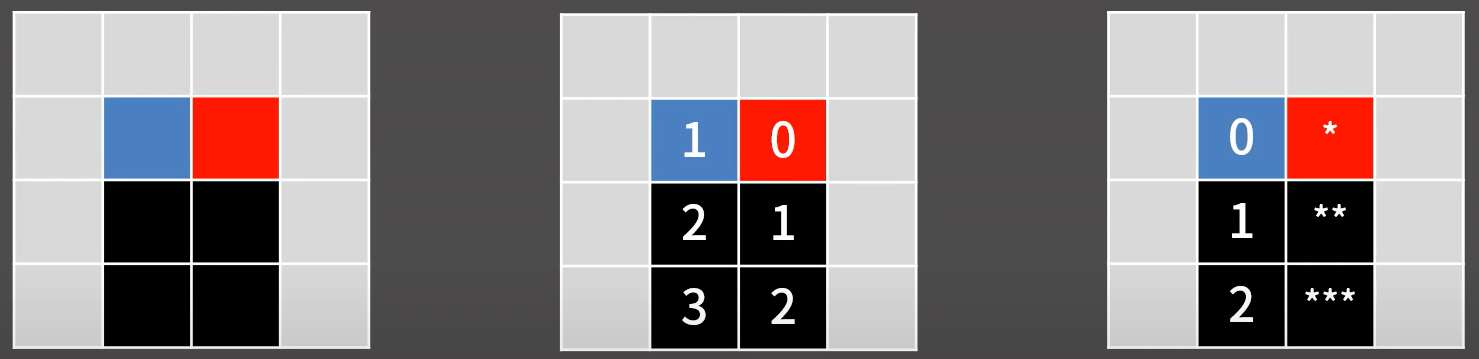
-
시작점의 종류가 다른 경우, 각 시작점에 대하여 BFS 수행
-
fire[][](불) : 좌표가 범위를 넘지 않으면서 벽(#)이 아니라면이전 좌표의 시간 + 1저장 -
move[][](지훈) : 좌표가 벽이 아니면서 지훈이가 도달한 시간이 불이 퍼지기 전인 경우이전 좌표의 시간 + 1저장 → 좌표가 범위를 넘으면 탈출한 것이므로 시간 출력 / 반복문이 종료되면 탈출하지 못한 것이므로IMPOSSIBLE출력
-
import java.io.*;
import java.util.*;
public class Main {
public static class Node {
int x, y;
public Node(int x, int y) {
this.x = x;
this.y = y;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int r = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
int[][] move = new int[r][c];
int[][] fire = new int[r][c];
Queue<Node> moveQ = new LinkedList<>();
Queue<Node> fireQ = new LinkedList<>();
for(int i=0;i<r;i++) {
String s = br.readLine();
for(int j=0;j<c;j++) {
char ch = s.charAt(j);
if(ch == 'J') {
move[i][j] = 1;
moveQ.offer(new Node(i, j));
}
else if(ch == 'F') {
fire[i][j] = 1;
fireQ.offer(new Node(i, j));
}
else {
move[i][j] = ch;
fire[i][j] = ch;
}
}
}
int[] dx = {-1, 1, 0, 0};
int[] dy = {0, 0, -1, 1};
Node tmp;
int px, py, nx, ny;
// 불 bfs
while(!fireQ.isEmpty()) {
tmp = fireQ.poll();
px = tmp.x; py = tmp.y;
for(int i=0;i<4;i++) {
nx = px + dx[i]; ny = py + dy[i];
if(nx < 0 || ny < 0 || nx > r-1 || ny > c-1) continue;
if(fire[nx][ny] == '.') {
fire[nx][ny] = fire[px][py] + 1;
fireQ.offer(new Node(nx, ny));
}
}
}
// 지훈 bfs
while(!moveQ.isEmpty()) {
tmp = moveQ.poll();
px = tmp.x; py = tmp.y;
for(int i=0;i<4;i++) {
nx = px + dx[i]; ny = py + dy[i];
if(nx < 0 || ny < 0 || nx > r-1 || ny > c-1) { // 탈출
System.out.println(move[px][py]); return;
}
if(move[nx][ny] != '#') {
if(move[px][py] + 1 < fire[nx][ny]) {
move[nx][ny] = move[px][py] + 1;
moveQ.offer(new Node(nx, ny));
}
}
}
}
// 탈출 실패
System.out.println("IMPOSSIBLE");
}
} : 2차원 배열 2개에 큐까지 2개 써서 그런지 메모리 초과 발생,, 인줄 알았으나 다른 사람들의 풀이를 봐도 다 2개씩 쓰고 통과하던데 나는 왜? 싶어서 GPT한테 물어봤는데,,
: 2차원 배열 2개에 큐까지 2개 써서 그런지 메모리 초과 발생,, 인줄 알았으나 다른 사람들의 풀이를 봐도 다 2개씩 쓰고 통과하던데 나는 왜? 싶어서 GPT한테 물어봤는데,,
 상상도 못한 답변 ㄴㅇㄱ.. 시간 비교에만 집중하느라 해당 좌표에 갔는지 표시를 안했던 것.. 그래서 같은 칸을 중복으로 탐색하다 보니 메모리 초과가 발생한 것.. 그래서 탐색한 불의 좌표를 -1로 표시하고 이후 해당 좌표가 -1이면 탐색하지 않도록 처리하니 성공!
상상도 못한 답변 ㄴㅇㄱ.. 시간 비교에만 집중하느라 해당 좌표에 갔는지 표시를 안했던 것.. 그래서 같은 칸을 중복으로 탐색하다 보니 메모리 초과가 발생한 것.. 그래서 탐색한 불의 좌표를 -1로 표시하고 이후 해당 좌표가 -1이면 탐색하지 않도록 처리하니 성공!
// 지훈 bfs
while(!moveQ.isEmpty()) {
tmp = moveQ.poll();
px = tmp.x; py = tmp.y;
for(int i=0;i<4;i++) {
nx = px + dx[i]; ny = py + dy[i];
if(nx < 0 || ny < 0 || nx > r-1 || ny > c-1) { // 탈출
System.out.println(move[px][py]); return;
}
if(move[nx][ny] != '#') {
// 방문하지 않았거나,
if(fire[nx][ny] != -1 && move[px][py] + 1 < fire[nx][ny]) {
move[nx][ny] = move[px][py] + 1;
fire[nx][ny] = -1; // 방문 표시
moveQ.offer(new Node(nx, ny));
}
}
}
}📝 예제 5 : 1차원에서의 BFS

- 그래프를 1차원 배열로 생성하여, 시작 위치에서
x+1,x-1,2x로 이동한 후 각 이동 위치에서 다시x+1,x-1,2x로 이동하는 방식으로 탐색을 수행하다가, 동생이 있는 위치에 도달하면 탐색을 종료한다.
import java.io.*;
import java.util.*;
public class Main {
static int[] graph = new int[100001];
static int s, e;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
s = Integer.parseInt(st.nextToken());
e = Integer.parseInt(st.nextToken());
System.out.println(bfs());
}
static int bfs() {
Queue<Integer> q = new LinkedList<>();
q.offer(s);
graph[s] = 1;
while(!q.isEmpty()) {
int tmp = q.poll();
if(tmp == e) return graph[tmp]-1;
if(tmp-1 >= 0 && graph[tmp-1] == 0) {
graph[tmp-1] = graph[tmp] + 1;
q.offer(tmp-1);
}
if(tmp+1 < 100001 && graph[tmp+1] == 0) {
graph[tmp+1] = graph[tmp] + 1;
q.offer(tmp+1);
}
if(tmp*2 < 100001 && graph[tmp*2] == 0) {
graph[tmp*2] = graph[tmp] + 1;
q.offer(tmp*2);
}
}
return 0;
}
}💡 DFS
Depth First Search : 다차원 배열을 탐색할 때, 깊이를 우선으로 탐색하는 알고리즘
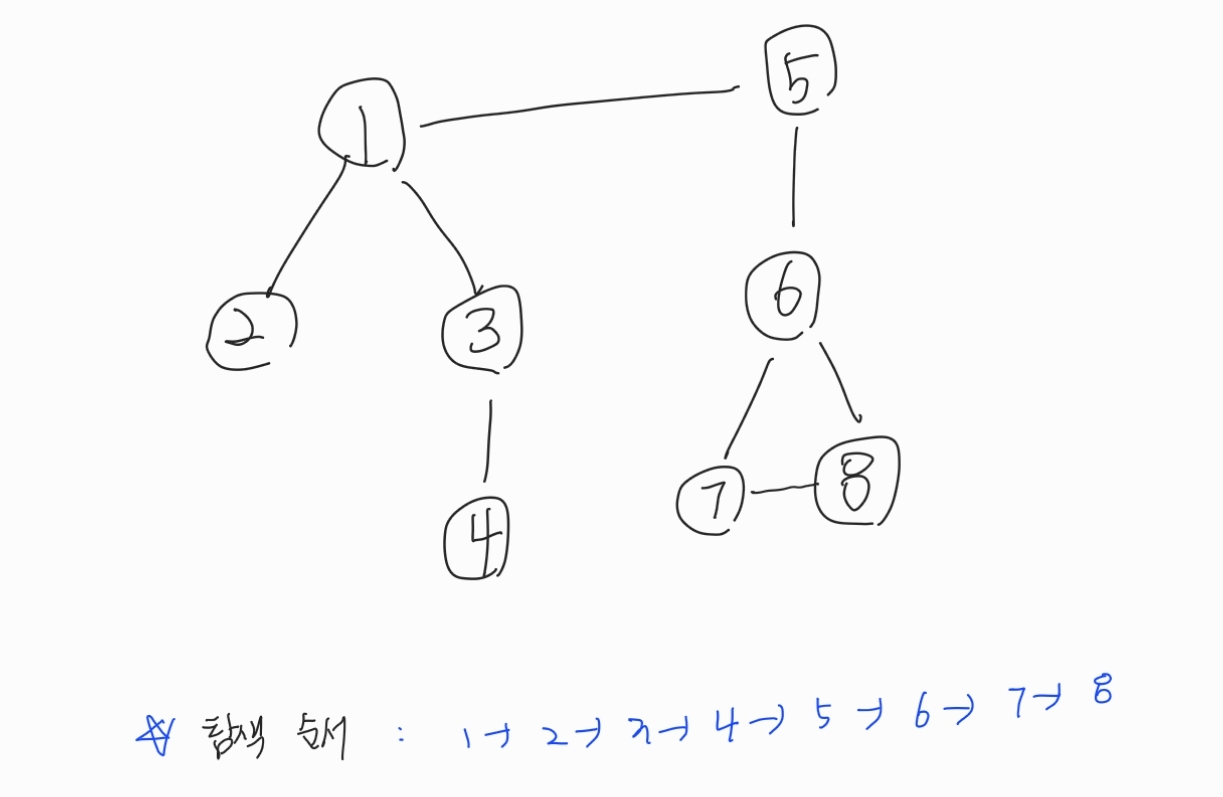
✅ 큐가 스택으로 변경된 것 외에는, BFS와 전체적인 흐름이 같다!
- 스택에 시작점을 넣고 방문 표시
- 스택의 꼭대기에 위치한 노드를 꺼내고 인접한 노드 탐색
2-1. 인접한 노드에 방문 표시가 없다면 스택에 넣고 방문 표시 후 2번 반복
2-2. 인접한 노드가 없거나 이미 방문했다면 2번 반복- 스택이 비면 탐색 종료
import java.io.*;
import java.util.*;
public class Main {
static int[][] graph = {{}, {2,3,5}, {1}, {1,4}, {3}, {1, 6}, {5, 7, 8}, {6, 8}, {6, 7}};
static boolean[] isVisit = new boolean[graph.length];
static StringBuilder sb = new StringBuilder();
public static void main(String[] args) throws IOException {
bfs(1);
System.out.println(sb);
}
static void bfs(int v) {
Stack<Integer> s = new Stack<>();
s.push(v);
isVisit[v] = true;
while(!s.isEmpty()) {
int idx = s.pop();
sb.append(idx + " ");
for(int i=graph[idx].length-1;i>=0;i--) {
int tmp = graph[idx][i];
if(!isVisit[tmp]) {
s.push(tmp);
isVisit[tmp] = true;
}
}
}
} : 스택은 후입선출이기 때문에, 순서를 맞추기 위해 각 노드에 인접한 노드를 역순으로 탐색
: 스택은 후입선출이기 때문에, 순서를 맞추기 위해 각 노드에 인접한 노드를 역순으로 탐색
📒 BFS vs DFS
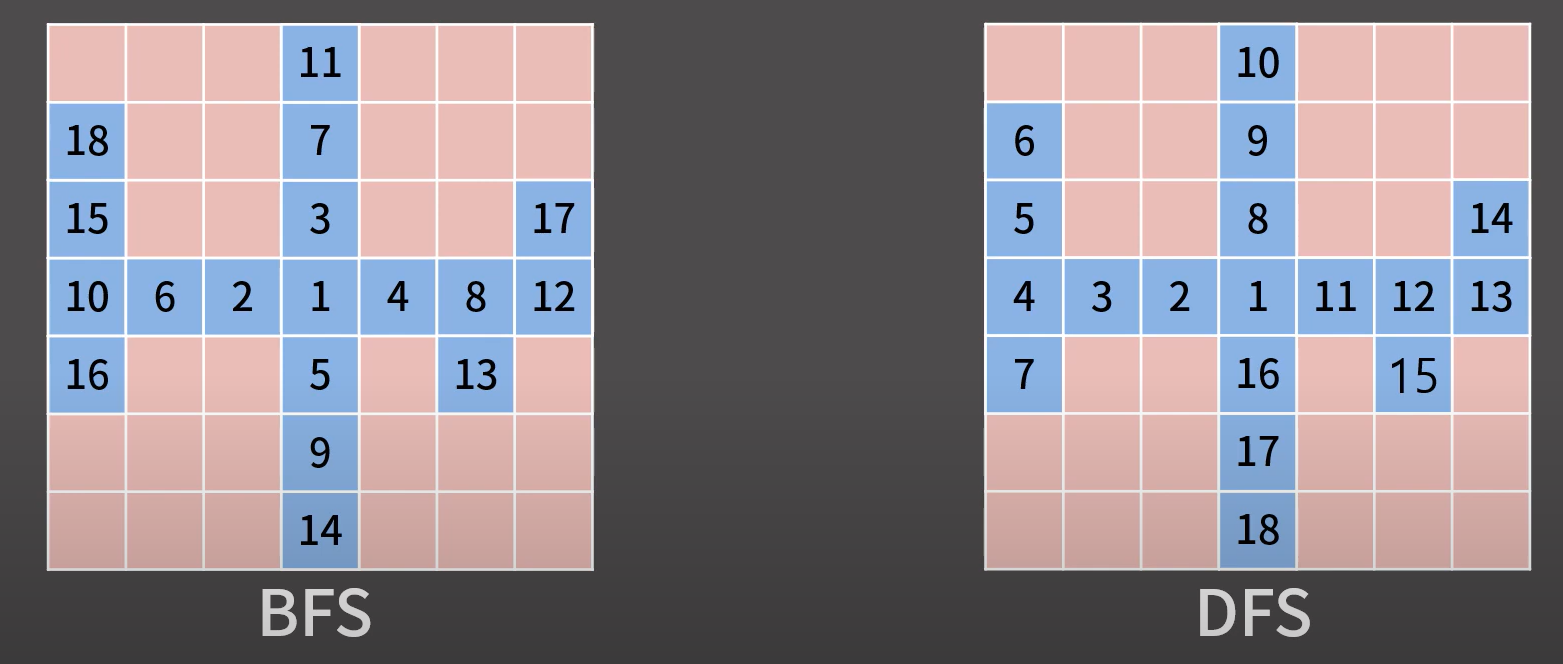
-
BFS : 시작점과 인접한 노드 모두 탐색 → 각 인접 노드와 인접한 노드 모두 탐색 → ...
-
DFS : 시작점과 인접한 노드 하나 탐색 → 한 노드와 인접한 노드의 탐색이 모두 끝난 후 시작점과 인접한 다른 노드 하나 탐색 → ...
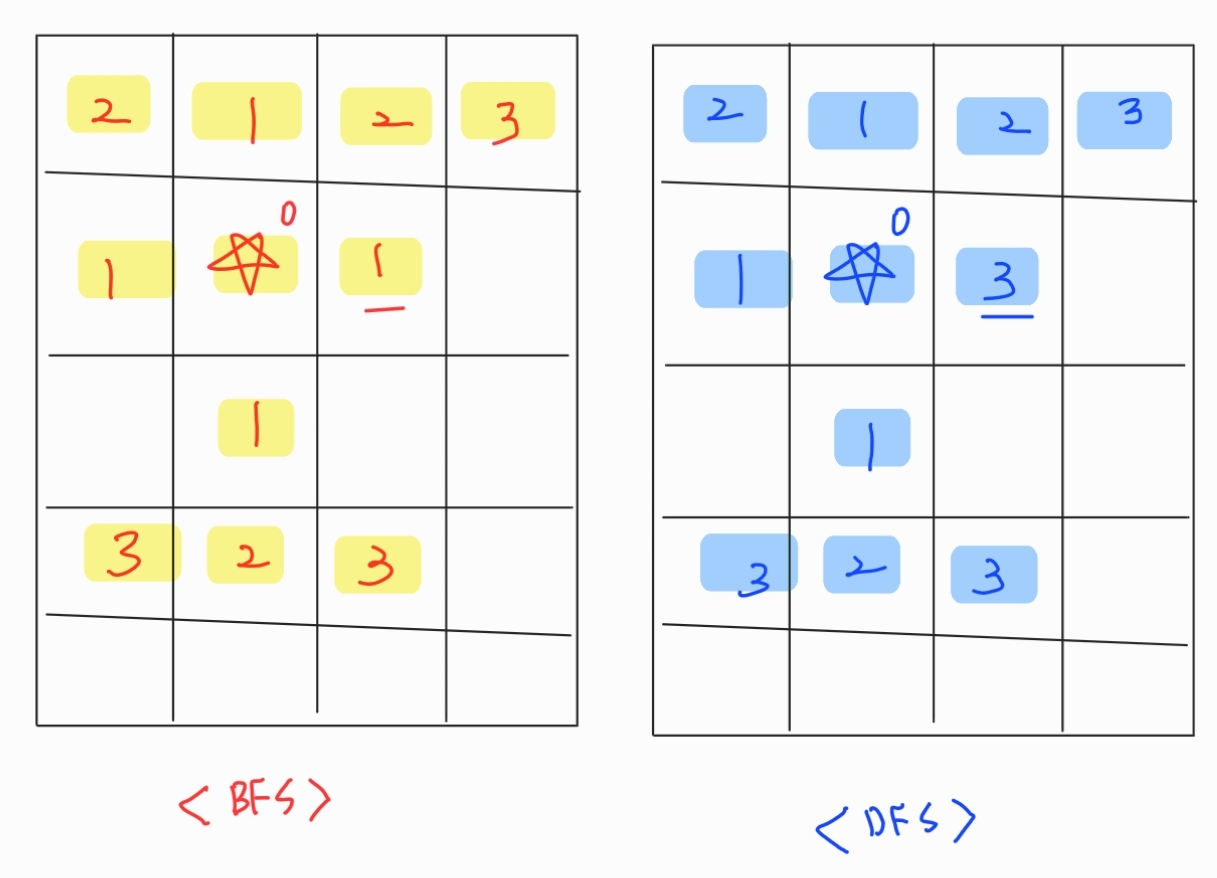
⭐ 거리 탐색 시, BFS에서는 시작점과 인접한 노드의 거리가 모두
+1이였지만 DFS는 해당 공식이 성립하지 않기 때문에 거리 탐색 시 사용할 수 없다!
🙇🏻♀️ 출처


