📌 문제 : 직사각형에서 탈출

[1085] 직사각형에서 탈출

한수는 지금 (x, y)에 있다. 직사각형은 각 변이 좌표축에 평행하고, 왼쪽 아래 꼭짓점은 (0, 0), 오른쪽 위 꼭짓점은 (w, h)에 있다. 직사각형의 경계선까지 가는 거리의 최솟값을 구하는 프로그램을 작성하시오.

⬇️ 입력

첫째 줄에 x, y, w, h가 주어진다.

⬆️ 출력

첫째 줄에 문제의 정답을 출력한다.

✔️ 제한

• 1 ≤ w, h ≤ 1,000
• 1 ≤ x ≤ w-1
• 1 ≤ y ≤ h-1
• x, y, w, h는 정수

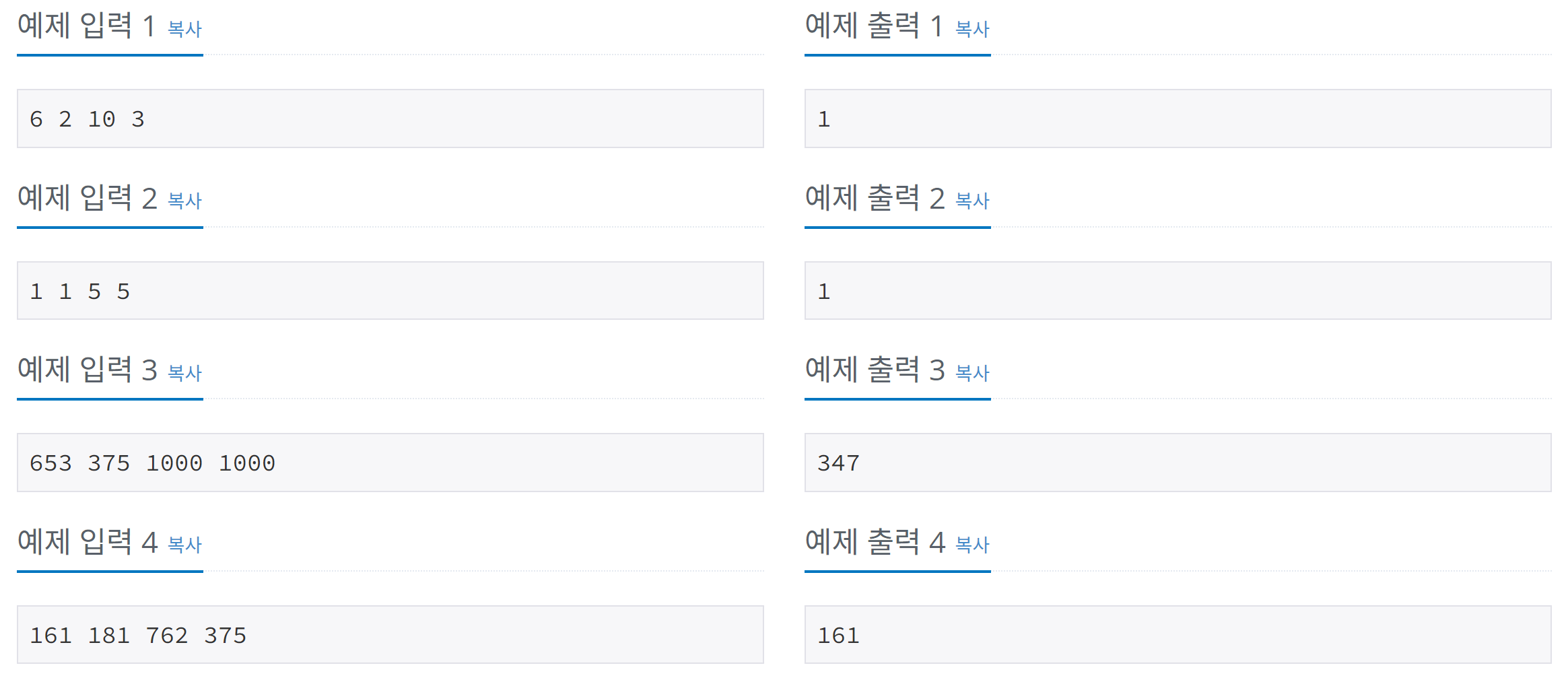
💡코드 : 직사각형에서 탈출

✅ 경계선까지의 최솟값 = 모서리까지의 최솟값

주어진 두 점이 (0, 0), (w, h)이고, 조건 1 ≤ x ≤ w-1, 1 ≤ y ≤ h-1에 따라 점 (x, y)는 두 점 안에 있다. x, w-x 중 x 좌표까지의 최솟값을 찾고, y, h-y 중 y 좌표까지의 최솟값을 찾은 후, 두 최솟값 중 더 작은 값을 최종 정답으로 출력한다.

import java.io.*;
import java.util.StringTokenizer;
public class Main {
	public static void main(String[] args) throws IOException {
		
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		
		StringTokenizer st = new StringTokenizer(br.readLine());
		int x = Integer.parseInt(st.nextToken());
		int y = Integer.parseInt(st.nextToken());
		int w = Integer.parseInt(st.nextToken());
		int h = Integer.parseInt(st.nextToken());
		
		int minX = (x > w-x) ? w-x : x;
		int minY = (y > h-y) ? h-y : y;
		bw.write(((minX > minY) ? minY : minX) + "");
		
		br.close();
		bw.close();
	}
}

(위 코드가 두번째 코드임! 첫번째 코드는 정리 전 버전,,)

---

📌 문제 : 네 번째 점

[3009] 네 번째 점

세 점이 주어졌을 때, 축에 평행한 직사각형을 만들기 위해서 필요한 네 번째 점을 찾는 프로그램을 작성하시오.

⬇️ 입력

세 점의 좌표가 한 줄에 하나씩 주어진다. 좌표는 1보다 크거나 같고, 1000보다 작거나 같은 정수이다.

⬆️ 출력

직사각형의 네 번째 점의 좌표를 출력한다.

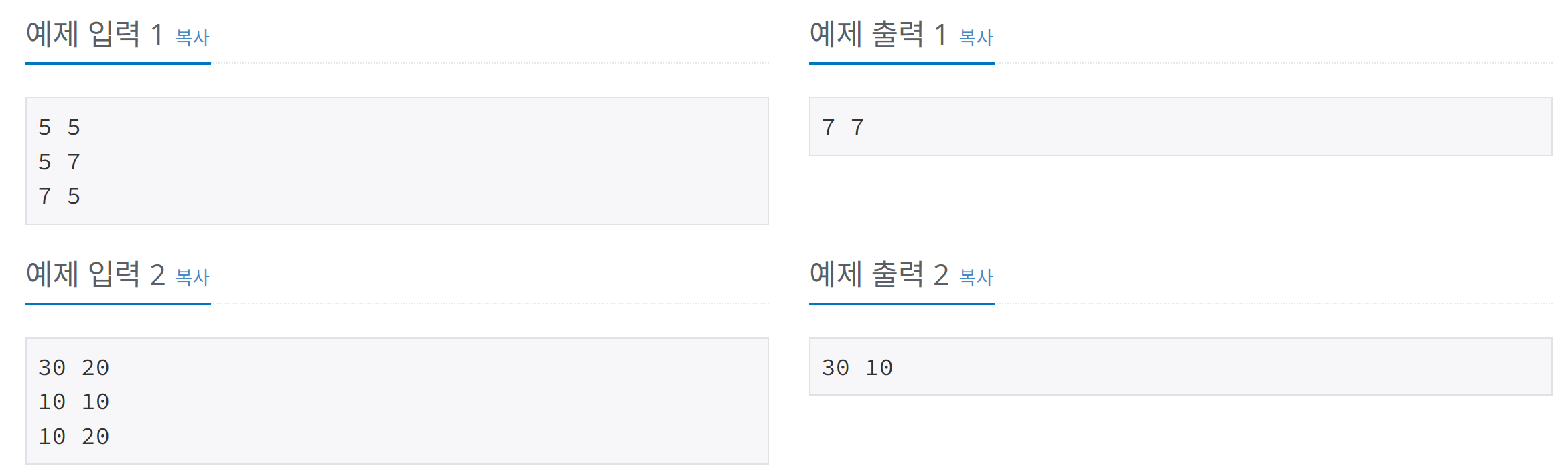
💡 코드 : 네 번째 점

✅ 네 점으로 직사각형을 만들기 위해서는 같은 값을 가지는 x와 y가 각각 두 쌍이여야 한다. 예를 들어, (5, 5), (5, 7), (7, 5), (7, 7) 의 경우 x는 5, 7이 각 2개, y는 5, 7이 각 2개로 이루어져 있다. 즉, 세 좌표의 x, y 값을 각각의 배열 x[], y[]에 담아 쌍을 이루지 않은 좌표를 찾아 새로운 점으로 도출할 수 있다. 이 때, x 좌표와 y 좌표를 찾는 과정이 같기 때문에 메서드 newDot(int[] arr)을 선언하여 해당 함수를 호출하는 방식으로 풀었다!

import java.io.*;
import java.util.StringTokenizer;
public class Main {
	
	static int newDot(int[] arr) {
		if(arr[0] == arr[1]) {
			return arr[2];
		} else if(arr[0] == arr[2]) {
			return arr[1];
		} else return arr[0];
	}
	
	public static void main(String[] args) throws IOException {
		
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		
		int[] x = new int[3];
		int[] y = new int[3];
		
		for(int i=0;i<3;i++) {
			StringTokenizer st = new StringTokenizer(br.readLine());
			x[i] = Integer.parseInt(st.nextToken());
			y[i] = Integer.parseInt(st.nextToken());
		}
		bw.write(newDot(x) + " " + newDot(y));
		
		br.close();
		bw.close();
	}
}