📌 문제

[1149] RGB 거리

RGB거리에는 집이 N개 있다. 거리는 선분으로 나타낼 수 있고, 1번 집부터 N번 집이 순서대로 있다.

집은 빨강, 초록, 파랑 중 하나의 색으로 칠해야 한다. 각각의 집을 빨강, 초록, 파랑으로 칠하는 비용이 주어졌을 때, 아래 규칙을 만족하면서 모든 집을 칠하는 비용의 최솟값을 구해보자.

• 1번 집의 색은 2번 집의 색과 같지 않아야 한다.
• N번 집의 색은 N-1번 집의 색과 같지 않아야 한다.
• i(2 ≤ i ≤ N-1)번 집의 색은 i-1번, i+1번 집의 색과 같지 않아야 한다.

⬇️ 입력

첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나 같은 자연수이다.

⬆️ 출력

첫째 줄에 모든 집을 칠하는 비용의 최솟값을 출력한다.

💡 코드

✅ 집을 칠하는 규칙이 3가지 주어졌는데, 결국 핵심은 이웃한 집과 색이 같으면 안된다는 것이다. 비용의 최솟값을 구해야 하므로, 세 가지 경우에 대한 결과값 중 최솟값을 구하면 된다. 이 때, 세 가지 경우란 N번째 집의 색이 0. 빨강 / 1. 초록 / 2. 파랑인 경우이다.

각 집을 색칠하는 데 드는 비용을 cost[][]에 저장하고, 세 가지 경우에 대한 비용을 dp[][]에 저장한다.

paint(n, color) 메서드는 집의 순서 n과 색깔 color를 매개변수로 전달받는다. 가장 먼저 main 메서드에서 N번째 집이 빨/파/초인 경우를 각각 호출하여, 마지막 집이 빨/파/초인 경우의 총 비용을 구한다.

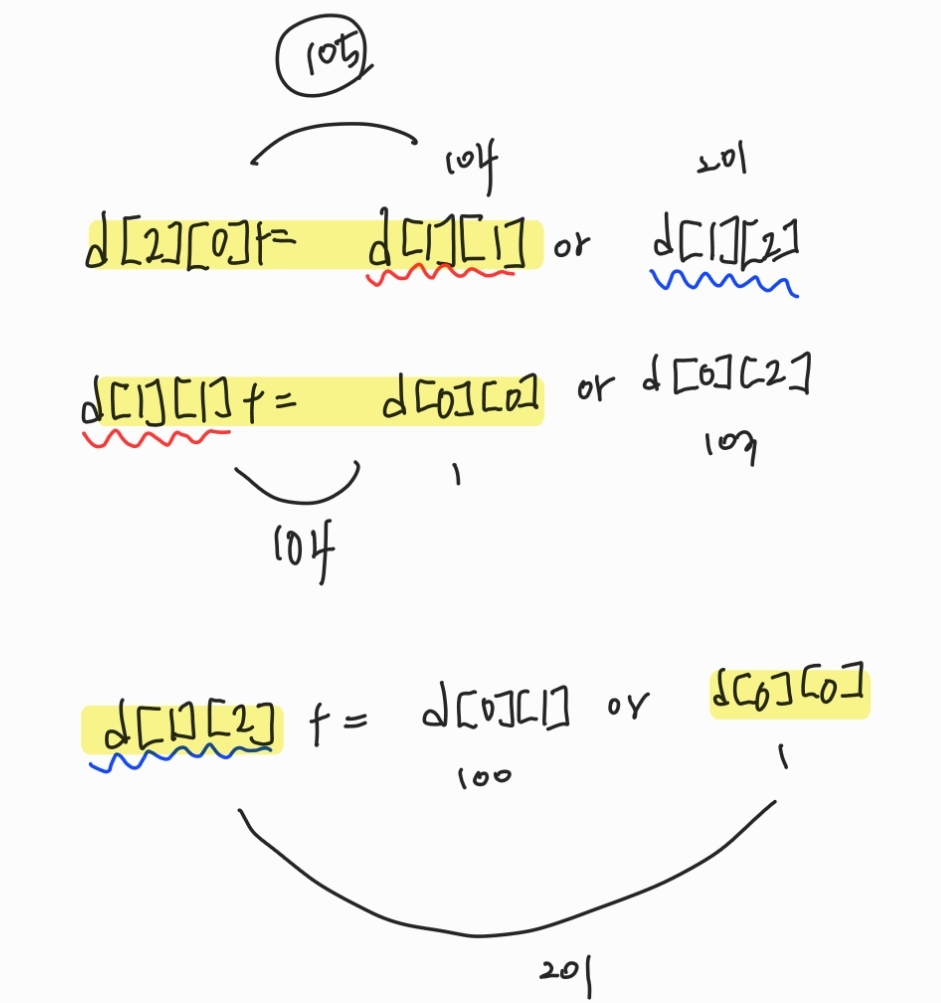
n번째 집의 최소 비용은 cost[n][color]에 해당하는 비용에 n-1번째 집의 이번 집의 색을 제외한 두 가지 색 중 최소 비용을 더해준다. 이를 점화식으로 표현하면 dp[n][[color] = cost[n][color] + Math.min(dp[n-1][다른 색1], dp[n-1][다른색2]) 이다. 이 때, 이전 집의 각 비용은 재귀 함수를 통해 호출할 수 있고, 해당 값을 계산할 때마다 dp[][]에 저장하여 다음에 호출되었을 때 바로 사용할 수 있게 한다. 만약 이미 계산되었다면 해당 값을 바로 리턴해주면 된다.

import java.io.*;
import java.util.*;
public class Main {
	
	static int[][] cost, dp;
			
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

		int n = Integer.parseInt(br.readLine());
		cost = new int[n][3];
		dp = new int[n][3];
		
		for(int i=0;i<n;i++) {
			StringTokenizer st = new StringTokenizer(br.readLine());
			
			cost[i][0] = Integer.parseInt(st.nextToken()); // R
			cost[i][1] = Integer.parseInt(st.nextToken()); // G
			cost[i][2] = Integer.parseInt(st.nextToken()); // B
		}
		
		dp[0][0] = cost[0][0];
		dp[0][1] = cost[0][1];
		dp[0][2] = cost[0][2];
		
		int result = Math.min(paint(n-1, 0), 
								Math.min(paint(n-1, 1), paint(n-1, 2)));
		
		bw.write(result + "");
		
		br.close();
		bw.close();
	}
	
	static int paint(int n, int color) {
		
		if(dp[n][color] == 0) {
			// 빨강
			if(color == 0)
				dp[n][color] = Math.min(paint(n-1, 1) , paint(n-1, 2)) + cost[n][color];
			
			// 초록
			else if(color ==  1)
				dp[n][color] = Math.min(paint(n-1, 0), paint(n-1, 2)) + cost[n][color];
			
			// 파랑
			else
				dp[n][color] = Math.min(paint(n-1, 0), paint(n-1, 1)) + cost[n][color];
		}
		
		return dp[n][color];
	}
}

✅ 재귀를 사용하여 해결하는 말고 반복문을 사용하는 방법으로도 풀어보았다!

재귀는 하향식 접근 방법이므로 처음 호출할 때 매개변수를 가장 큰 문제인 n번째 집으로 시작해서 이전 단계의 함수를 차례로 호출하여 해결하였는데, 반복문은 상향식 접근 방법이므로 첫 시작을 작은 문제인 2번째 집에서 시작하였다. 접근 방향만 다르지 계산 로직은 dp[n][[color] = cost[n][color] + Math.min(dp[n-1][다른 색1], dp[n-1][다른색2])으로 같다!

import java.io.*;
import java.util.*;
public class Main {
	
	static int[][] cost, dp;
			
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

		int n = Integer.parseInt(br.readLine());
		cost = new int[n][3];
		dp = new int[n][3];
		
		for(int i=0;i<n;i++) {
			StringTokenizer st = new StringTokenizer(br.readLine());
			
			cost[i][0] = Integer.parseInt(st.nextToken()); // R
			cost[i][1] = Integer.parseInt(st.nextToken()); // G
			cost[i][2] = Integer.parseInt(st.nextToken()); // B
		}
		
		dp[0][0] = cost[0][0];
		dp[0][1] = cost[0][1];
		dp[0][2] = cost[0][2];
		
		paint(n);
		int result = Math.min(dp[n-1][0], Math.min(dp[n-1][1], dp[n-1][2]));
		
		bw.write(result + "");
		
		br.close();
		bw.close();
	}
	
	static void paint(int n) {
		for(int i=1;i<n;i++) {
			dp[i][0] = cost[i][0] + Math.min(dp[i-1][1], dp[i-1][2]); // 빨
			dp[i][1] = cost[i][1] + Math.min(dp[i-1][0], dp[i-1][2]); // 초
			dp[i][2] = cost[i][2] + Math.min(dp[i-1][0], dp[i-1][1]); // 파
		}
	}
}