💡 복잡도 (Complexcity)

알고리즘의 성능을 객관적으로 평가하는 기준 : 시간 / 공간

✅ 효율적인 알고리즘 : 입력값이 커짐에 따라 증가하는 시간의 비율을 최소화한 알고리즘

---

📒 시간 복잡도 (Time Complexcity)

실행에 필요한 시간을 평가한 것

✏️ 시간 복잡도 표기법

• 빅 오메가 (Big-Ω) : 최상의 실행 시간 = 최소 이정도 시간이 걸림
• 빅 세타 (Big-θ) : 평균 실행 시간
• 빅 오 (Big-O) : 최악의 실행 시간 = 아무리 오래 걸려도 이 시간보다는 덜 걸림 ➡️ 가장 많이 사용

---

📝 빅오 표기법 (Big-O notation)

알고리즘이 수행되는 최악의 시나리오를 표현 → 주어진 식의 최고차항으로 나타냄

---

🔹 O(1) : 상수 시간 (Constant Time)

입력 크기(N)에 상관없이 일정한 연산을 수행하는 경우

static void func(int n) {
	System.out.prinln(n); 
}

: n에 상관없이 무조건 한 번 출력 ➡️ O(1)

🔹 O(logN) : 로그 시간 (Logarithmic Time)

입력 크기(N)가 커질 때, 연산 횟수가 logN에 비례하여 증가하는 경우 = 연산이 한 번 실행될 때마다 데이터의 크기가 절반 감소하는 경우 ➡️ Binary Search (이진 탐색), Tree 형태 자료구조

for(int i=1;i<=n;i*2) { // log2 n + 1 : 마지막 조건문 검사까지 수행
	System.out.prinln(n); // i = 1 -> 2 -> 4 -> ... : log2 n
}

: log2 n + 1 + log2 n = 2log2 n + 1 ➡️ O(log n)

🔹 O(N) : 선형 시간 (Linear Time)

입력 크기(N)가 커질 때, 연산 횟수가 n에 비례하여 선형적으로 증가하는 경우 ➡️ 단일 for문

for(int i=0;i<n;i++) { // n + 1 : 마지막 조건문 검사까지 수행
	System.out.prinln(n); // 실행 횟수 = 반복 횟수 = n 
}

: (n+1) + n = 2n + 1 ➡️ O(n)

🔹 O(NlogN)

O(n) ➕ O(logN) ➡️ 퀵/병합/힙 정렬

for(int i=i;i<n;i++) { // n
	for(int j=1;j<n;j*2) { // log n + 1
    	System.out.prinln(n); // log n
    }
}

: n + n * (log n + 1 + log n) = 2n + 2nlog n ➡️ O(nlog n)

🔹 O(n^2) : 2차 시간 (Quadratic Time)

입력 크기(n)가 커질 때, 연산 횟수가 n^2에 비례해서 증가하는 경우 ➡️ 이중 for문, 삽입/버블/선택 정렬

for(int i=1;i<n;i++) { // n
	for(int j=1;j<n;j++) { // n
    	System.out.prinln(n); // n-1
    }
}

: n + n * (n + n - 1) = 2n^2 ➡️ O(n^2)

🔹 O(2^n) : 지수 시간 (Exponential Time)

입력 크기(n)가 커질 때, 연산 횟수가 2^n에 비례해서 증가하는 경우 ➡️ 재귀 알고리즘, 피보나치 수열

int func(int n) {
	if(n <=1) return n;
    return func(n-1) + func(n-2); 
}

: 함수를 한 번 호출할 때마다 두 번씩 재귀함수 호출 ➡️ O(2^n)

---

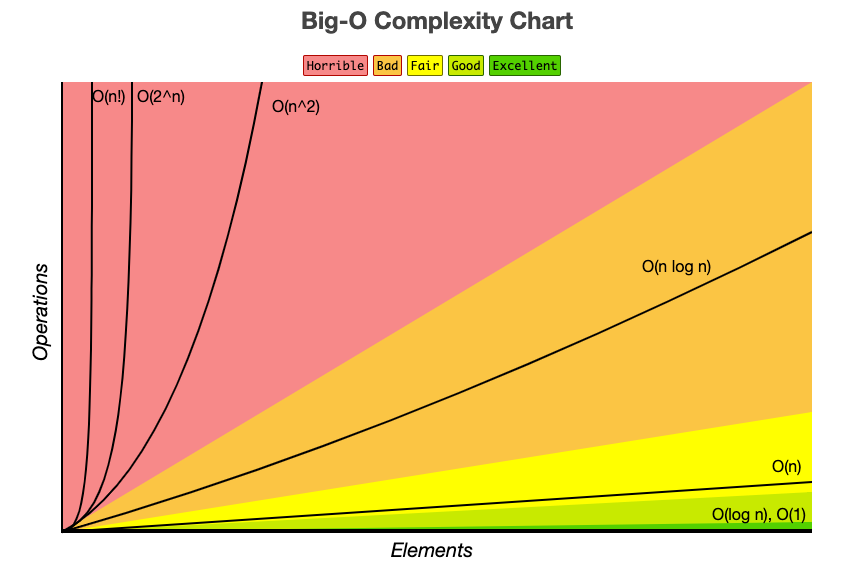
• O(1) < O(logN) < O(N) < O(NlogN) < O(N^2) < O(2^N) < O(N!)
  : 오른쪽으로 갈수록 시간 복잡도가 크다 = 수행 시간이 오래 걸린다!

---

➕ 허용 범위

코딩 테스트 시, 입력의 크기에 따라 통과할 수 있는 시간 & 공간 복잡도

• 시간 복잡도

⭐ 문제를 풀기 전에, 입력 크기를 보고 시간 복잡도를 생각한 후 코드를 구현해야 한다!

n	허용 시간 복잡도
n <= 11	O(N!)
n <= 25	O(2^N)
n <= 100	O(N^4)
n <= 500	O(N^3)
n <= 3,000	O(N^2logN)
n <= 5,000	O(N^2)
n <= 1,000,000	O(NlogN)
n <= 10,000,000	O(N)
그 이상	O(logN), O(1)

• 공간 복잡도

  ⭐ 512MB = 1.2억개의 int를 저장할 수 있는 공간 (int 하나에 4byte)

🙇🏻‍♀️ 참고 : [바킹독의 실전 알고리즘] 0x01강 - 기초 코드 작성 요령 I