[프로그래머스, 파이썬] 가장 먼 노드 - Level 3 | 다익스트라(Dijkstra) 알고리즘 문제

📌 프로그래머스 레벨3 - 가장 먼 노드

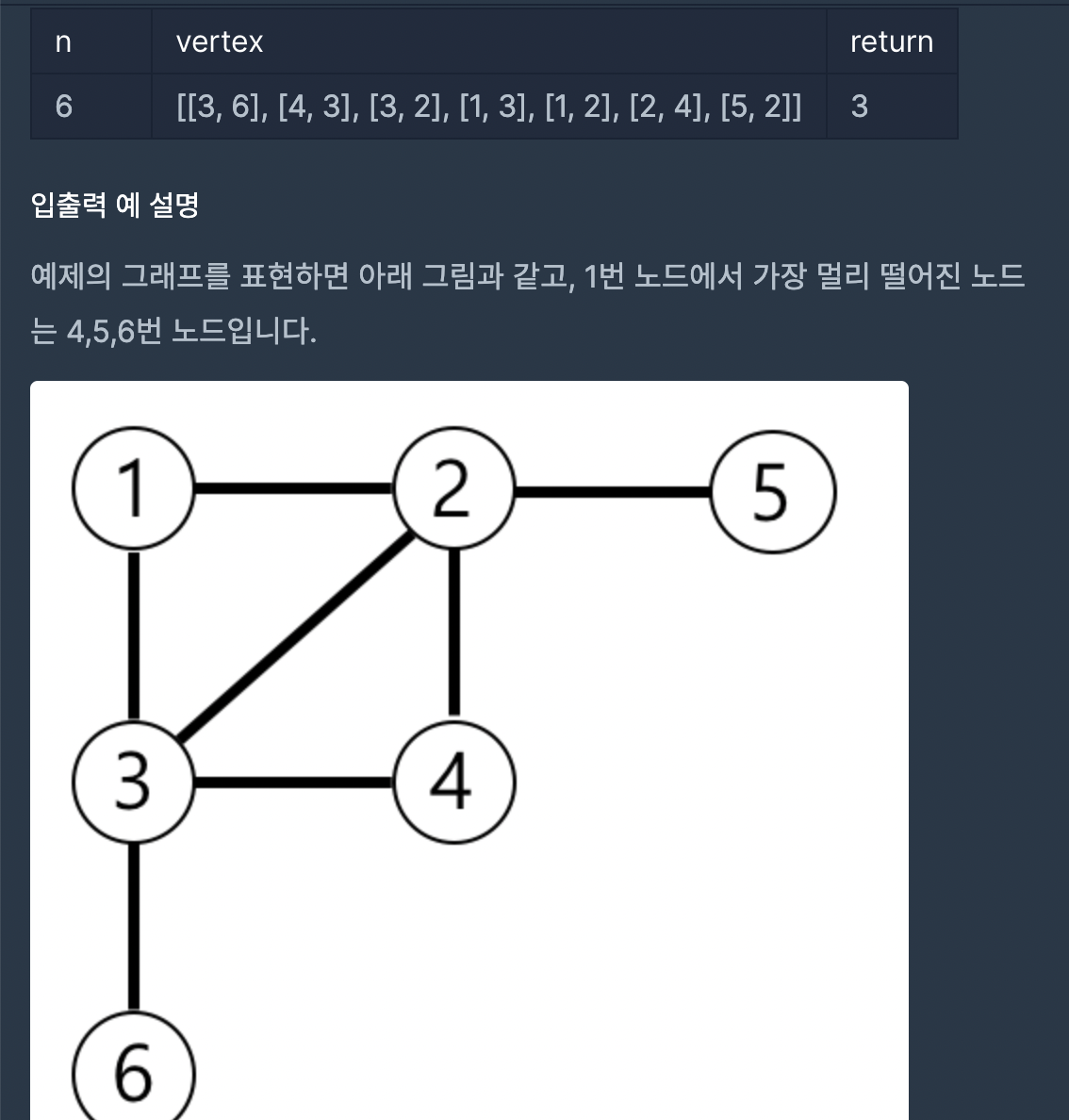
1에서부터 각 노드까지(2,3,4,...n)의 최단 거리들을 구해주고, 그 최단거리 중에 최댓값을 가지는 노드의 수를 구하는 문제이다.

📣 다익스트라 알고리즘

최단거리가 최대값인 것을 구하라? == 다익스트라를 사용해라

다익스트라(Dijkstra) 알고리즘?

특정한 하나의 지점에서 모든 지점까지의 최단 거리를 알아낼 수 있는 알고리즘.

각 지점의 거리를 최댓값 혹은 무한대로 지정해놓고, 과정을 거치며 최단거리를 갱신해준다.

보통 내가 사용하는 다익스트라 알고리즘의 파이썬 코드의 Form은 다음과 같다.

from collections import defaultdict, deque
# node = 문제와 같이 [[연결노드1,연결노드2],....] 꼴일 때,

def solution(node):
	# defaultdict을 사용하면 key가 존재하지 않아도 값을 새로 채워넣을 수 있어서 편하다.
    graph = defaultdict(list)
	# 각 노드까지의 거리
    distance = [INF for _ in range(len(node)+1)]
   	# index수랑 노드 번호 맞추려고.
    distance[0] = 0
    distance[시작노드] = 1
    
	for i,j in node:
    	graph[i].append(j)
        graph[j].append(i)
        
    # 시작노드, 거리 카운트 1부터 시작
    q = deque([[시작노드, 1]])
    
    while q:
    	p, cnt = q.popleft()
        
        ~~최단 거리 갱신 알고리즘~~~
  

이 문제는 다익스트라를 사용하는 기본적인 문제다. 사실 다익스트라 알고리즘을 알고 있다면 쉽게 풀리는 문제!

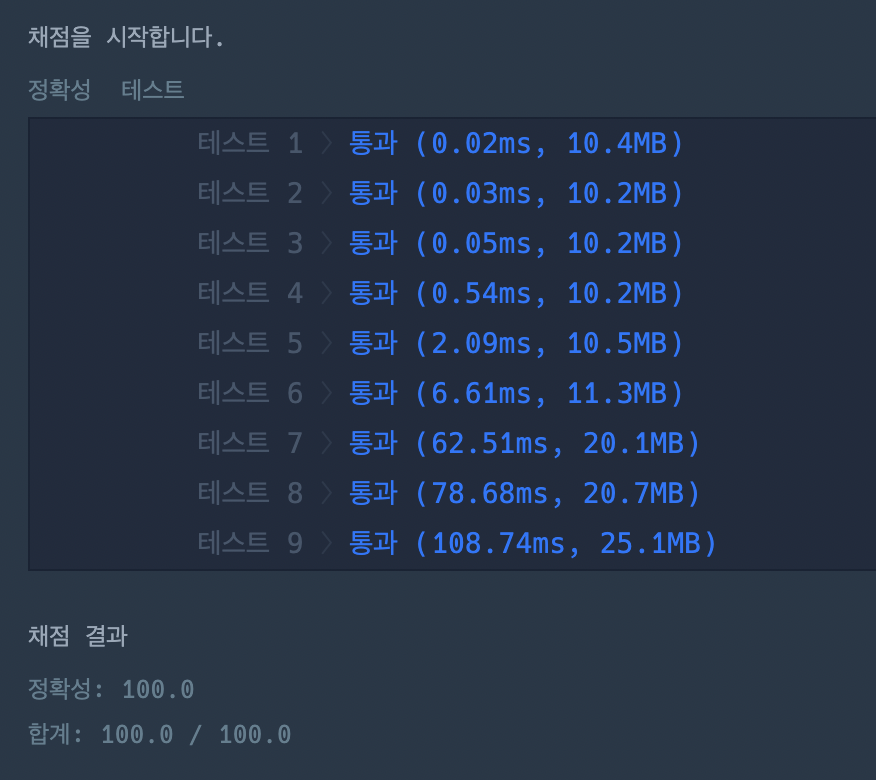
📝 내 답안 1 (Lastest)

from collections import defaultdict,deque
def solution(n, edge):
    answer = 0
    node = defaultdict(list)
    for i,j in edge:
        node[i].append(j)
        node[j].append(i)
        
    visit = [50001 for _ in range(n+1)]
    visit[0] = 0
    visit[1] = 0
    
    q = deque([[1,1]])
    
    while q:
        p,cnt = q.popleft()
        
        for i in node[p]:
            if cnt < visit[i]:
                visit[i] = cnt
                q.append([i,cnt+1])
                    
    visit.sort(reverse = True)
    M = visit[0]
    for i in visit:
        if i == M:
            answer += 1
        else:
            break
            
    return answer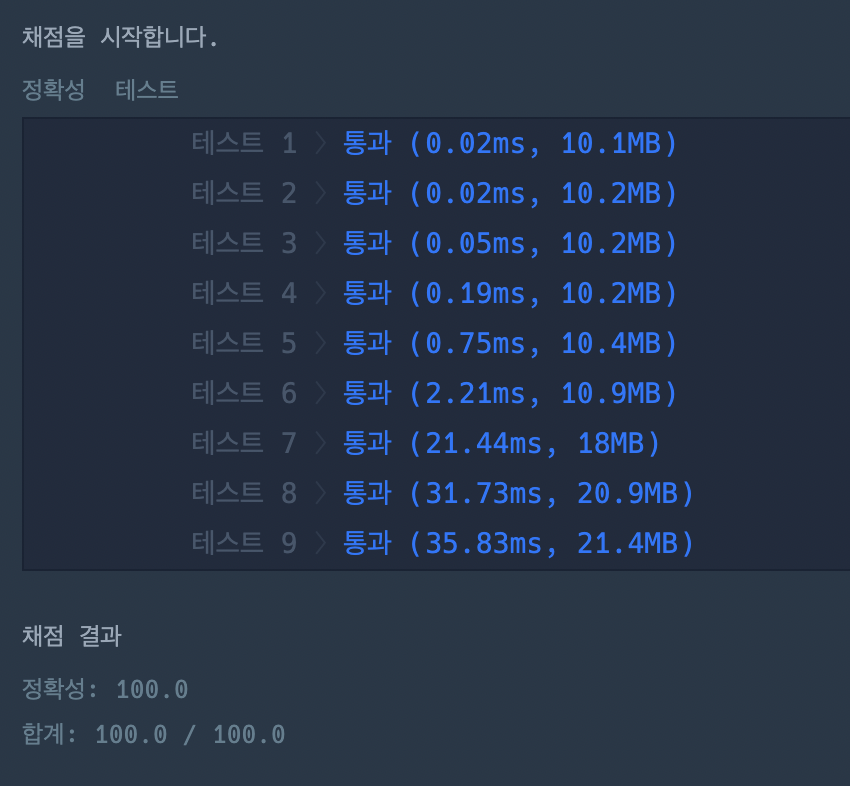

📝 내 답안 2

이건 예전에 내가 풀었던 답안인데, 확실히 최근에 푼 답안이 더 빠르다.

이런 소소한 성취가 나를 뿌듯하게 만든다...ㅎㅎ

from collections import defaultdict,deque

def solution(n, edge):
    answer = 0
    graph = defaultdict(list)
    INF = 50001
    visit = [INF for _ in range(n+1)]
    visit[0] = 0
    visit[1] = 0
    edge.sort()
    
    for a,b in edge:
        graph[a].append(b)
        graph[b].append(a)
    
    #node,cnt 배열
    q = deque()
    
    for i in graph[1]:
        q.append([i,1])
    
    while q:
        node, cnt = q.popleft()
        
        #현재 경로가 최단경로 일 때
        if cnt < visit[node]:
            visit[node] = cnt
            
            cnt += 1
            for i in graph[node]:
                #출발점인 1이 아니면
                if visit[i] != 0:
                    q.append([i,cnt])
    visit.sort(reverse = True)
    MAX = max(visit)
    for i in visit:
        if i == MAX:
            answer+=1
        else:
            break
    return answer