[프로그래머스, 파이썬] 등대 - 레벨 3 | BFS

📌 프로그래머스 Level 3 : 등대

한 뱃길의 양쪽 끝 등대 중 적어도 하나는 켜져 있도록 등대를 켜 두어야 합니다.

이 문구를 자세히 기억해 두자.

📝 내 답안

from collections import defaultdict,deque
def solution(n, lighthouse):
    graph = defaultdict(list)
    onoff = [0 for _ in range(n + 1)]

    for a, b in lighthouse:
        graph[a].append(b)
        graph[b].append(a)

    q = deque()
    # 리프 노드 담기
    for i in range(1, n+1):
        if len(graph[i]) == 1:
            q.append(i)

    # 리프 노드부터 루트까지 올라가기, 등대 켜지면 다음 노드와 연결 끊기
    while q:
        now_leaf = q.popleft()
        if graph[now_leaf] == []:
            break
        parent = graph[now_leaf][0]

        # 리프 노드 그래프에서 삭제
        del graph[now_leaf]
        # 부모 노드에서 리프 노드 연결 해제
        graph[parent].remove(now_leaf)
        # 부모 노드가 리프 노드가 되면 큐에 넣기
        if len(graph[parent]) == 1:
            q.append(parent)

        if onoff[now_leaf] == 1:
            continue
        onoff[parent] = 1
    
    return sum(onoff)

🔮 풀이

다음 알고리즘에 따라 풀었다.

1. 그래프, 등대 켜짐 유무 판단할 리스트 생성

    graph = defaultdict(list)
    onoff = [0 for _ in range(n + 1)]

    for a, b in lighthouse:
        graph[a].append(b)
        graph[b].append(a)

2. 우선 초기 리프 노드 큐에 담기

    q = deque()
    # 리프 노드 담기
    for i in range(1, n+1):
        if len(graph[i]) == 1:
            q.append(i)

3. BFS : 리프 노드와 부모 노드 check
- onoff 갱신, 리프 노드와 부모 노드 연결 해제를 통해 리프 노드 갱신해나가기

    # 리프 노드부터 루트까지 올라가기, 등대 켜지면 다음 노드와 연결 끊기
    while q:
        now_leaf = q.popleft()
        # 만약 현재 리프노드가 비어있으면(끝)
        if graph[now_leaf] == []:
            break
       
        # 부모 노드
        parent = graph[now_leaf][0]

        # 리프 노드를 그래프에서 삭제
        del graph[now_leaf]
        # 부모 노드에서 리프 노드 연결 해제
        graph[parent].remove(now_leaf)
        
        # 부모 노드가 리프 노드가 되면 큐에 넣기
        if len(graph[parent]) == 1:
            q.append(parent)
            
		'''
        현재 리프 노드에 해당하는 등대가 켜져있지 않으면 
        부모 노드 등대를 키기
        '''
        if onoff[now_leaf] == 1:
            continue
        onoff[parent] = 1

한 뱃길의 양쪽 끝 등대 중 적어도 하나는 켜져 있도록 등대를 켜 두어야 합니다.

이 말은 무조건 3개의 노드가 있을 때 가운데 노드가 켜져있어야 함을 의미한다.
예를 들어서,

n = 8
lighthouse = [[1,2],[2,3],[1,4],[4,5],[1,6],[6,7],[7,8]]

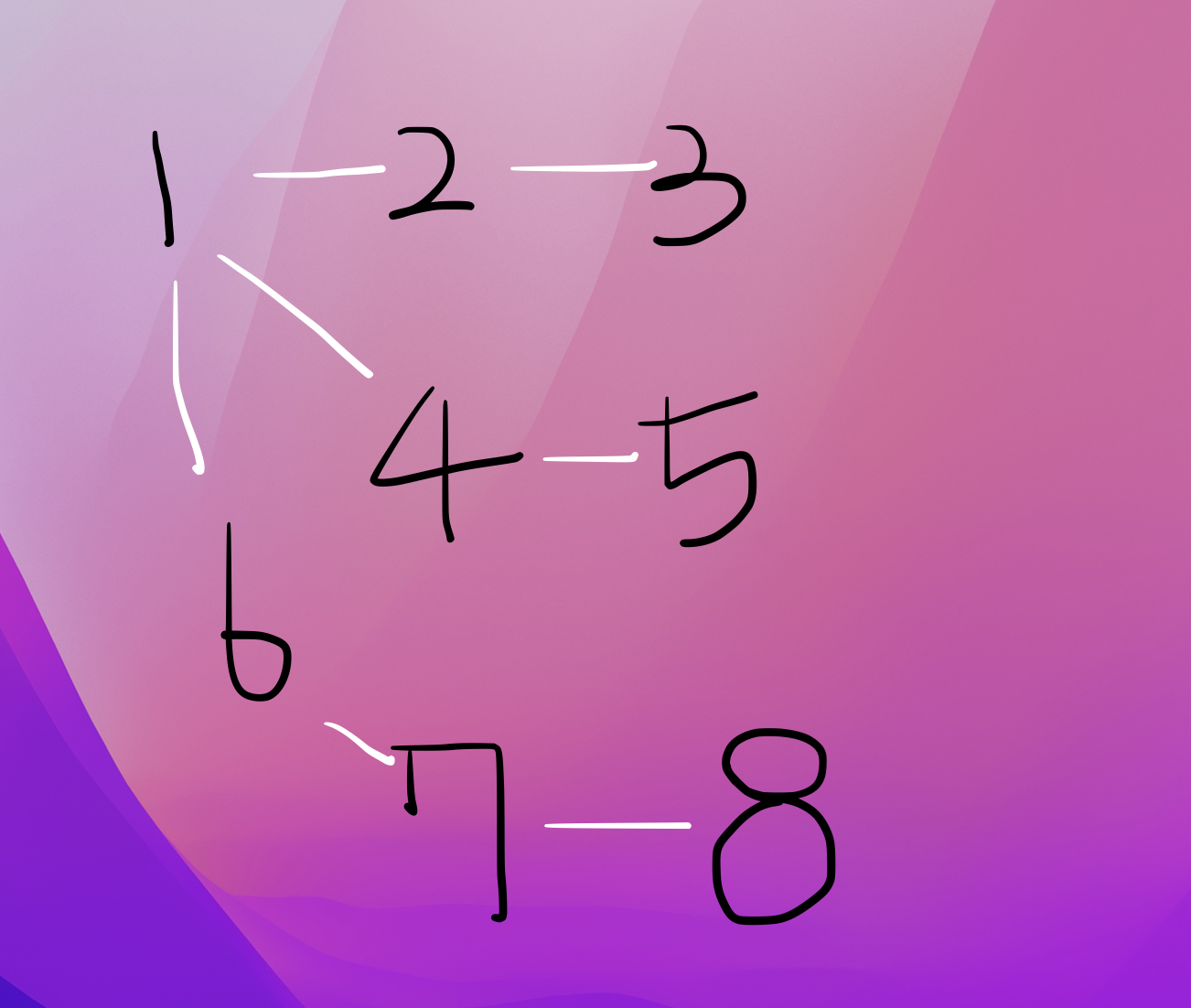
여기서에 다음 2,4,7번 등대만 켜지면 되는게 아니다.

왜냐햐면 한 뱃길의 양쪽 끝 등대 중 적어도 하나는 켜져 있도록 등대를 켜 두어야 합니다. 라는 문제 제시 때문이다.

이 문제는 인근 등대가 다 켜져야하는 문제가 아니라!
등대와 등대 사이 뱃길 의 불이 켜져야하는 문제이다..

위와 같이 2,4,7만 켜지면 1번 6번 사이의 뱃길의 불이 켜질 수 없어서,

아래와 같이 1번 등대도 켜져야 한다.

이렇게 이해하고 구현하면 풀리는 문제..

구현보다 문제 해석 때문에 시행착오를 겪었다.