[프로그래머스, 파이썬] 표현 가능한 이진트리 - 레벨 3 | DFS

📌 프로그래머스 Level 3 : 표현 가능한 이진트리

포화 이진트리에 대해 정확하게 이해를 못해서 한창 헤맸는데,

그거만 빼면 구현 난이도는 높지 않았던 문제!

처음에 헷깔렸던게, 포화 이진트리가 모든 노드에서 높이, 즉 depth가 같아야하는 줄 몰라서 조금 어렵게 생각했다.

포화 이진트리는 높이(depth)가 일정하다 는 부분을 염두에 두고 DFS로 풀면 쉽게 풀린다.

📝 내 답안

def solution(numbers):
    answer = [1 for _ in range(len(numbers))]
    n = []
    
    for num in numbers:
        v = format(num,"b")
        nn = len(v)
        init = 1
        i = 1
        while init < nn:
            i += 1
            init = 2**i -1
        # index 1부터 사용하기 위해 '0' 하나를 더 붙여줌
        n.append('0'+'0'*(init-nn)+v)

    def dfs(node,start,end):
        nonlocal result
        root = (start+end)//2
        if root%2 == 1:
            return
        left = start + (root-start)//2
        right = end - (end-root)//2
        if node[root] == '0' and (node[left] == '1' or node[right] == '1'):
            result = 0
            return
        dfs(node,root+1,end)
        dfs(node,start,root-1)
        
    # 루트 트리가 0인데 서브가 1 경우를 찾기(dfs)
    for i in range(len(n)):
        node = n[i]
        nn = len(node)-1
        result = 1
        dfs(node,1,nn)
        if result == 0:
            answer[i] = 0
        
    return answer

🔮 풀이

다음 알고리즘에 따라 풀었다.

1. 해당 수를 이진수로 변환하기
2. 변환한 이진수의 길이를 포화 이진트리 길이에 맞추어 왼쪽부터 '0' 추가
   2^n - 1 이 포화 이진트리 노드 갯수임을 명심하기

depth = 2일 때
2^2 - 1 = 3

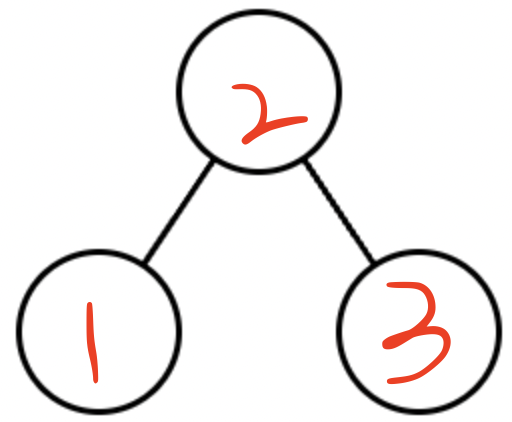
depth = 3일 때
2^3 - 1 = 7

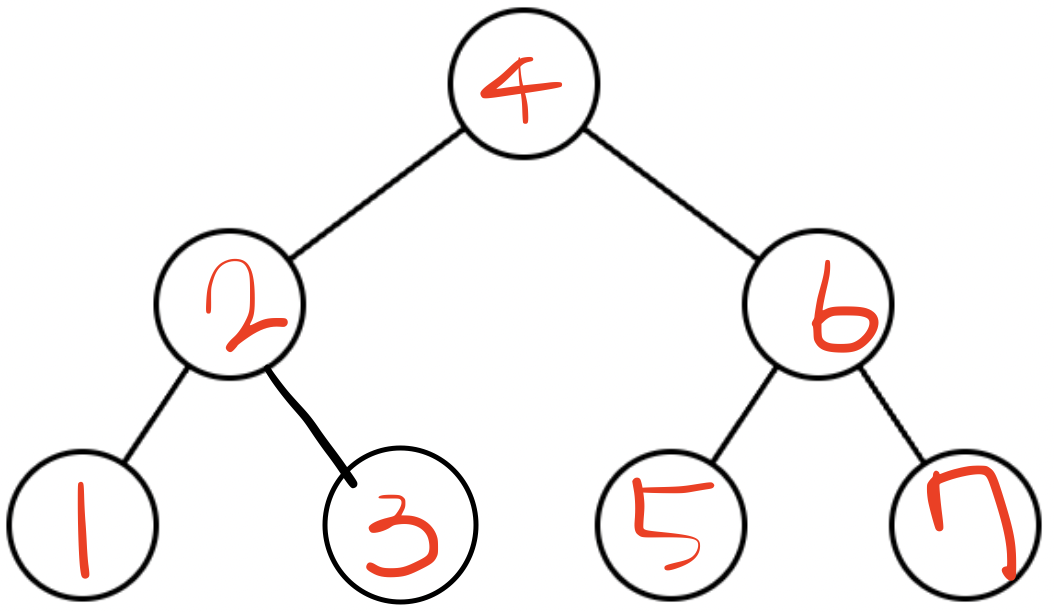
    for num in numbers:
    	# 이진수로 변환해준다, 문자열로 반환함
        v = format(num,"b")
        # 현재 변환된 이진수의 길이
        nn = len(v)
        # 사용할 포화 이진트리 노드 갯수를 구하기 위한 초기 세팅
        init = 1
        # i는 트리의 depth.
        i = 1
        
        while init < nn:
        	'''
            depth를 1개 증가시키고 노드 갯수를 갱신시켜 
            사용할 포화 이진트리 노드 갯수를 찾기
            '''
            i += 1
            init = 2**i -1
        # index 1부터 사용하기 위해 '0' 하나를 더 붙여줌(편의상)
        n.append('0'+'0'*(init-nn)+v)

3. DFS 사용 : 부모 노드가 0인데 자식 노드가 1이면 포화 이진트리를 만들 수 없는 수이다.

    def dfs(node,start,end):
        nonlocal result
        root = (start+end)//2
        # 현재 부모노드가 홀수인 것은 리프 노드(맨 하위 노드)이므로 끝내기
        if root%2 == 1:
            return
        # 왼쪽 자식 노드
        left = start + (root-start)//2
        # 오른쪽 자식 노드
        right = end - (end-root)//2
        # 부모 노드는 0인데 자식 노드들 중에 1을 가진 것이 있으면 X
        if node[root] == '0' and (node[left] == '1' or node[right] == '1'):
            result = 0
            return
        # 오른쪽 노드 탐색
        dfs(node,root+1,end)
        # 왼쪽 노드 탐색
        dfs(node,start,root-1)
        
    # 루트 트리가 0인데 서브가 1 경우를 찾기(dfs)
    for i in range(len(n)):
        node = n[i]
        # 편의상 0 하나 더 붙였기 때문에 실제 길이에서 하나 빼준게 우리가 사용할 길이
        nn = len(node)-1
        result = 1
        dfs(node,1,nn)
        if result == 0:
            answer[i] = 0