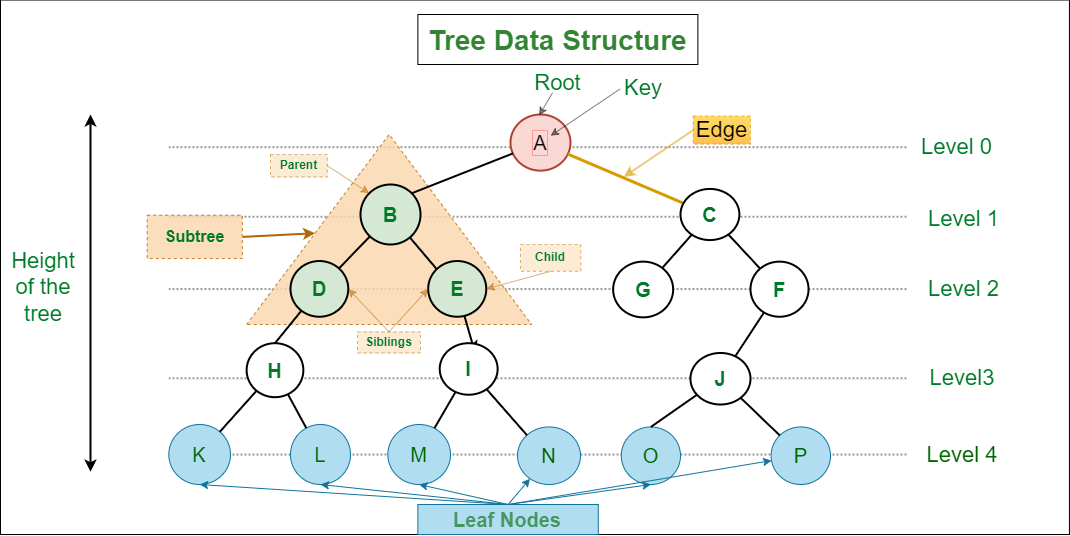
Tree 트리
트리(Tree)는 계층적 데이터 구조를 모델링하는데 사용되는 추상 데이터 타입(ADT). 트리는 비선형구조.
Node : 트리를 이루는 모든 개별 데이터.
Root : 트리의 시작점이 되는 첫 번째 노드(가장 상위 부모). 단말노드(Terminal Node).
Parent : 노드의 상위 노드. 내부노드(Internal Node). 노드는 하나의 부모노드만 가짐.
Child : 노드의 하위에 연결된 노드. 노드는 0개 또는 1개이상의 자식노드를 가질 수 있음.
Edge : 한 노드와 다른 노드를 연결하는 링크(간선).
Leaf Node : 트리에서 자식이 없는 노드(가장 하위 자식).
Depth : 루트 노드에서 어떤 노드까지 도달하기 위해 거쳐야하는 간선의 수.
Level : 루트(0레벨)에서 몇번째 깊이인지 나타냄. 같은 depth를 가지고 있는 노드를 묵어 같은 레벨로 표혀할 수 있음.
Degree : 한 노드에서 뻗어나온 간선의 수(자식 노드의 수). 0개 또는 1개 이상.
Tree Height : 루트노드에서 리프노드까지의 최대 간선의 수.
Height : 어떤 노드와 리프노드의 사이의 최대 간선의 수.
Tree Size : 트리의 노드 수.
Size : 자신을 포함한 모든 자손의 노드의 개수.
Sub Tree : 노드와 그 노드의 자손으로 구성된 트리.
Path : 한 노드에서 다른 노드로 갈 때 거쳐가는 노드들의 순서.
Tree Traversal 트리 순회
모든 노드를 한번에 하나씩 방문하여 트리를 통과하는 것을 Traversal라고 함. Array나 Linked List는 선형 데이터 구조이므로, 첫번재 요소에서 마지막 요소에 도착할 수 있는 방법은 하나뿐이지만, 트리는 다른 방향으로 분기될 수 있으므로(비선형 데이터 구조), 트리를 횡단하는 방법은 다양하다.
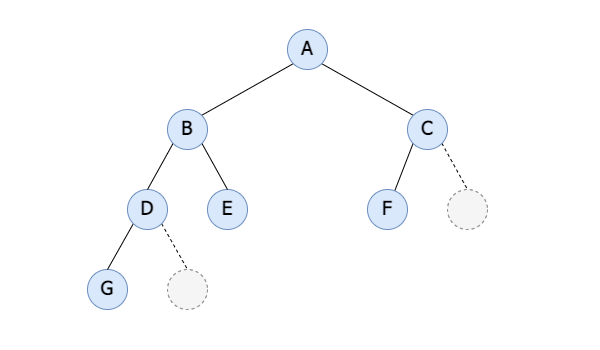
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
# 이진 트리 생성
root = TreeNode('A')
root.left = TreeNode('B')
root.right = TreeNode('C')
root.left.left = TreeNode('D')
root.left.right = TreeNode('E')
root.right.left = TreeNode('F')
root.left.left.left = TreeNode('G')너비 우선 탐색(BFS, Breadth-First Search)
같은 레벨의 노드들을 모두 방문한 다음 다음 레벨의 노드들을 방문하는 것. Queue를 사용하여 구현함.
레벨 순서 순회(Level order traversal)
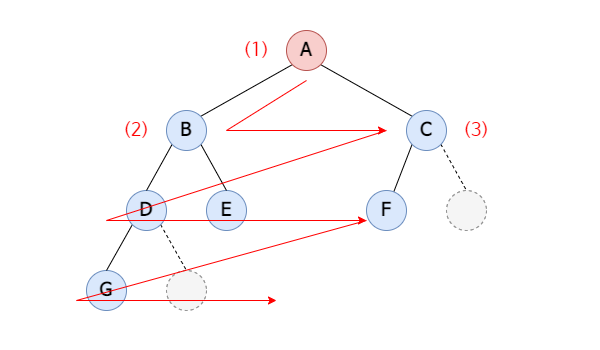
순회 결과는 A → B → C → D → E → F → G
def level_order_traversal(root):
if root is None:
return
# 노드를 저장할 큐 생성
queue = deque()
# 루트 노드를 큐에 추가
queue.append(root)
# 큐가 빌 때까지 반복
while queue:
# 현재 레벨의 노드 개수를 저장
level_length = len(queue)
# 현재 레벨의 모든 노드를 방문하고, 다음 레벨의 노드를 큐에 추가
for _ in range(level_length):
# 현재 레벨에서 가장 왼쪽에 있는 노드를 꺼냄
node = queue.popleft()
# 현재 노드를 방문
print(node.value, end=" ")
# 현재 노드의 왼쪽 자식을 큐에 추가
if node.left:
queue.append(node.left)
# 현재 노드의 오른쪽 자식을 큐에 추가
if node.right:
queue.append(node.right)깊이 우선 탐색(DFS, Depth-First Search)
가능한 한 깊숙이 노드를 탐색하고, 갈 수 있는 길이 끝나면 이전 분기점으로 돌아가 다른 경로를 탐색하는 방법.
Stack를 사용하거나 재귀적으로 구현함.
전위순회(Preorder traversal)
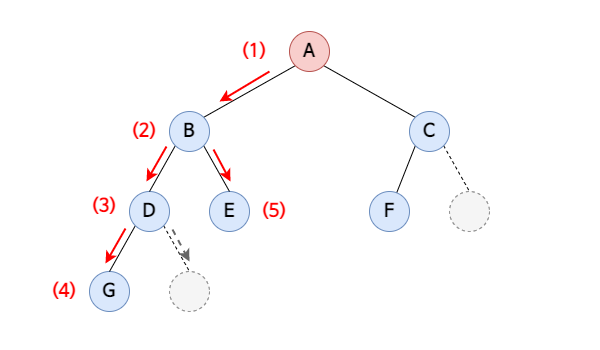
루트 노드를 먼저 방문하고, 왼쪽 서브트리를 순회한 후, 오른쪽 서브트리를 순회.
방문순서 : 루트 -> 왼쪽 -> 오른쪽
순회 결과는 A → B → D → G → E → C → F
def preorder_traversal(node):
if node is not None
# 현재 노드를 방문
print(node.value, end=" ")
# 왼쪽 서브트리를 전위 순회
preorder_traversal(node.left)
# 오른쪽 서브트리를 전위 순회
preorder_traversal(node.right)중위순회(Inorder traversal)
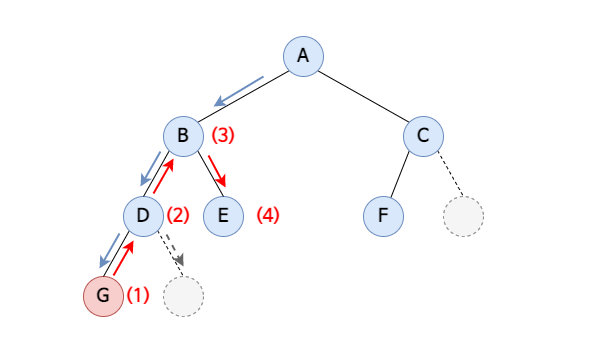
왼쪽 서브트리를 순회한 후, 루트 노드를 방문하고, 오른쪽 서브트리를 순회.
방문 순서 : 왼쪽 -> 루트 -> 오른쪽
순회 결과는 G → D → B → E → A → F → C
def inorder_traversal(node):
if node is not None:
# 왼쪽 서브트리를 중위 순회
inorder_traversal(node.left)
# 현재 노드를 방문
print(node.value, end=" ")
# 오른쪽 서브트리를 중위 순회
inorder_traversal(node.right)하위순회(Postorder traversal)
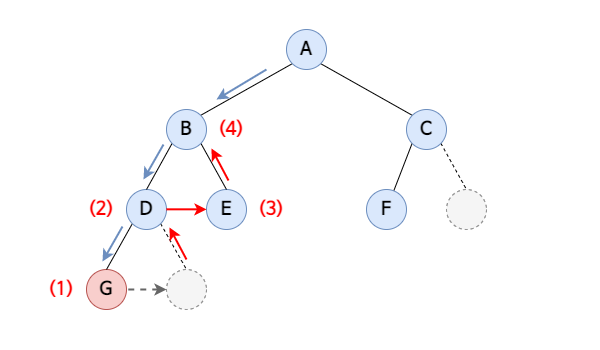
왼쪽 서브트리와 오른쪽 서브트리를 방문한후 마지막으로 루트 노드를 방문.
방문 순서 : 왼쪽 -> 오른쪽 -> 루트
순회 결과는 G → D → E → B → F → C → A
def postorder_traversal(node):
if node is not None:
# 왼쪽 서브트리를 하위 순회
postorder_traversal(node.left)
# 오른쪽 서브트리를 하위 순회
postorder_traversal(node.right)
# 현재 노드를 방문
print(node.value, end=" ")Tree의 주요 유형
Binary Tree 이진 트리
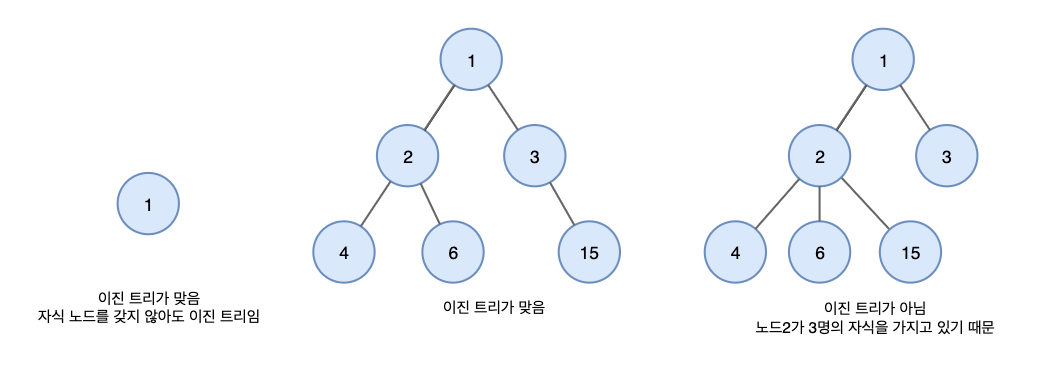
각 노드가 최대 2개의 자식노드(왼쪽 자식 노드와 오른쪽 자식 노드)를 가질 수 있는 트리 데이터 구조의 한 유형.
탐색, 검색, 삽입 및 삭제와 같은 알고리즘은 이해하기 쉽고 구현하기 쉽고 실행속도가 빨라짐.
Binary Tree vs Arrary, LinkedList
예를 들어 1000개의 원소 배열 중 700번 원소처럼 원소에 직접 접근하려면 배열이 빠름. 그러나 원소를 삽입하고 삭제하려면 메모리에서 다른 원소가 이동하여 새로운 원소를 배치하거나 삭제된 원소를 대체해야 하므로 시간이 많이 걸린다.
Linked List는 노드를 삽입하거나 삭제할 때 빠르며 메모리 이동이 필요하지 않지만 목록 내부의 요소에 액세스하Binary Tree는 노드에 액세스하는 속도가 빠르고 노드를 삭제하거나 삽입하는 속도가 빠르기 때문에 메모리 이동이 필요하지 않음.
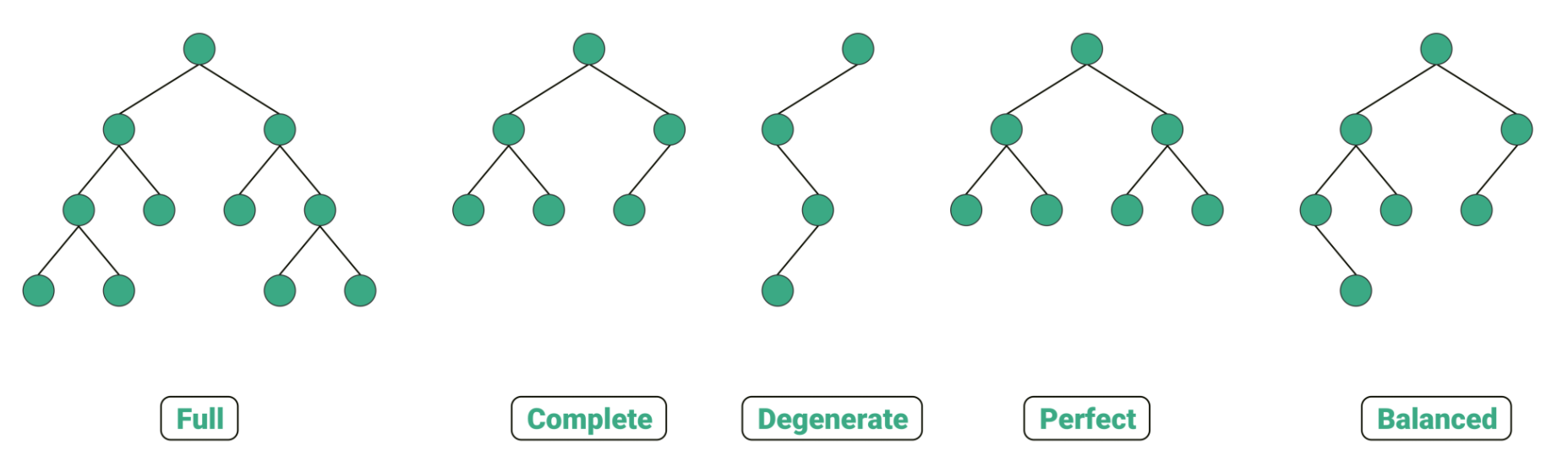
Full Binary Tree 정 이진 트리
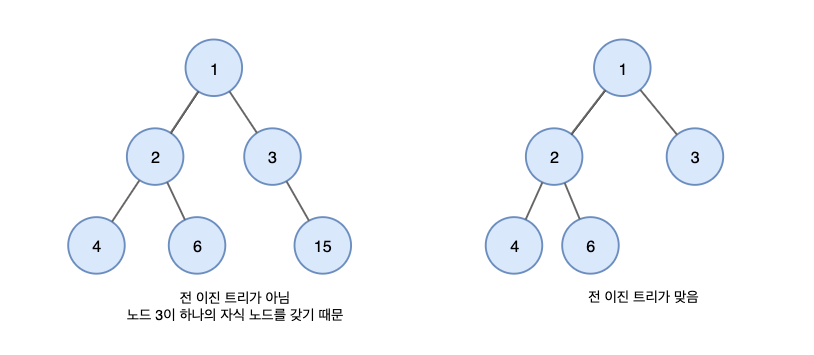
정 이진 트리는 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리.
Complete Binary Tree 완전 이진 트리
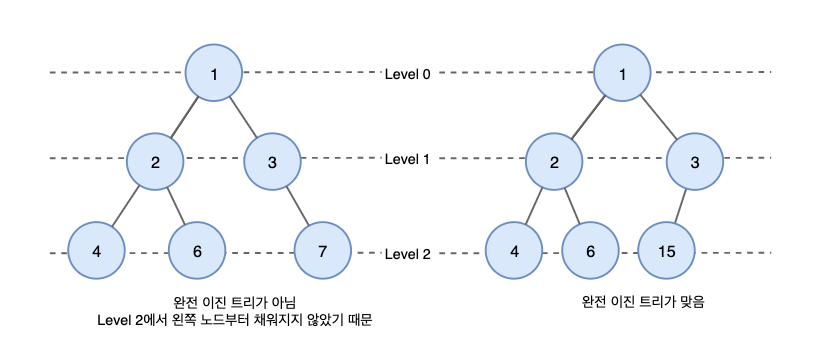
마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있는 트리. 마지막 레벨은 노드로 꽉 차 있지 않아도 되지만 노드가 왼쪽에서 오른쪽으로 채워져야함. 힙과 관련.
Degenerate Binary Tree 변질 이진 트리
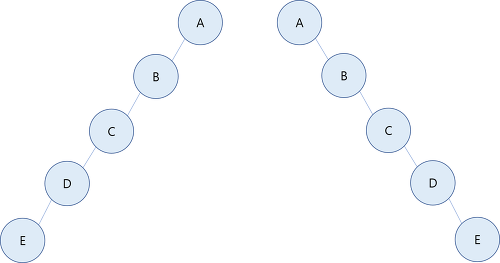
같은 높이의 이진 트리 중에서 최소 갯수의 노드수를 가지며 왼쪽 혹은 오른쪽 서브트리만을 가지는 이진트리. 모든 노드가 왼쪽에만 있거나 오른쪽에만 있는 트리. 편향 이진 트리(Skewed Binary Tree/Pathological Binary Tree)라고도 함.
Perfact Binary Tree 포화 이진 트리
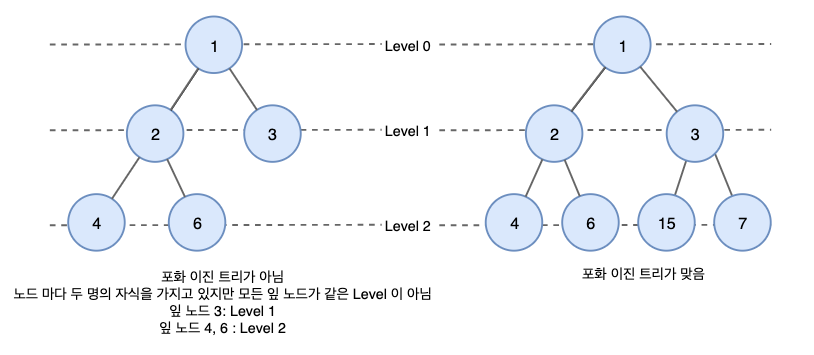
포화 이진 트리는 모든 리프 노드가 동일한 레벨에 있으며, 모든 레벨이 노드로 가득 차 있는 트리. 모든 내부 노드는 두 개의 자식 노드를 가지고 있음.
Balanced Binary Tree 균형 이진 트리
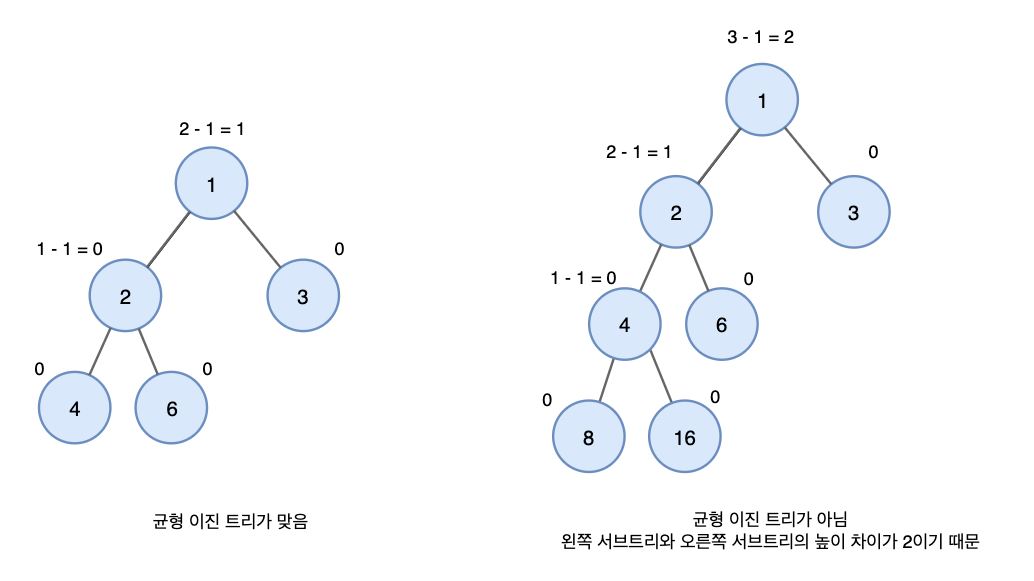
균형 이진 트리는 트리의 각 노드에 대해 왼쪽 및 오른쪽 부분 트리 높이 사이의 차이가 최대 1만큼 나는 트리.
이진 탐색 트리 (BST, Binary Search Tree)
각 노드에 대해 왼쪽 자식 노드가 낮은 값을 가지며 오른쪽 자식 노드가 높은 값을 갖는 이진 트리 유형.
이진 검색 트리의 장점은 검색, 삭제 및 삽입과 같은 작업이 빠르고 메모리에서 값을 이동할 필요없이 수행됨.
이진 탐색 트리의 검색
def search(node, target): # 루트노드에서 시작
if node is None:
return None
elif node.data == target: # 타겟노드이면 return
return node
elif target < node.data: # 타겟노드의 값이 더 낮으면 왼쪽 하위 트리에서 검색
return search(node.left, target)
else: # 타겟노드의 값이 더 높으면 오른쪽 하위 트리에서 검색
return search(node.right, target)이진 탐색 트리의 삽입
def insert(node, data): # 루트노드에서 시작
if node is None: # 비교할 오른쪽/왼쪽 노드가 없을때까지
return TreeNode(data)
else:
if data < node.data: # 값이 더 낮으면
node.left = insert(node.left, data) # 왼쪽으로 이동
elif data > node.data: # 값이 더 높으면
node.right = insert(node.right, data) # 오른쪽으로 이동
return node이진 탐색 트리에서 최솟값을 가진 노드 찾기
def minValueNode(node):
current = node
while current.left is not None: # 가능한한 왼쪽으로 이동
current = current.left
return current이진 탐색 트리의 삭제
def delete(node, data):
if not node:
return None
if data < node.data: # 삭제하려는 값이 현재 노드의 data보다 작은경우, 왼쪽 서브트리에서 재귀적으로 삭제 시도
node.left = delete(node.left, data)
elif data > node.data: # 삭제하려는 값이 현재 노드의 data보다 큰 경우, 오른쪽 서브트리에서 재귀적으로 삭제 시도
node.right = delete(node.right, data)
else:
# 자식노드가 없거나 하나인 경우, 해당 노드를 삭제하고 자식 노드를 부모노드에 연결함. 자식이 없는 경우 None
if not node.left:
temp = node.right
node = None
return temp
elif not node.right:
temp = node.left
node = None
return temp
# 자식 노드가 2개 있는 경우. 오른쪽 서브트리에서 최소값을 가진 노드를 찾아 그 값을 삭제할 노드의 위치로 복사함. 복사된 값을 가진 노드를 오른쪽 서브트리에서 삭제
node.data = minValueNode(node.right).data
node.right = delete(node.right, node.data)
return node| Data Structure | Searching for a value | Delete / Insert leads to shifting in memory |
|---|---|---|
| Sorted Array | O(log n) | Yes |
| Linked List | O(n) | No |
| Binary Search Tree | O(log n) | No |