문제
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.
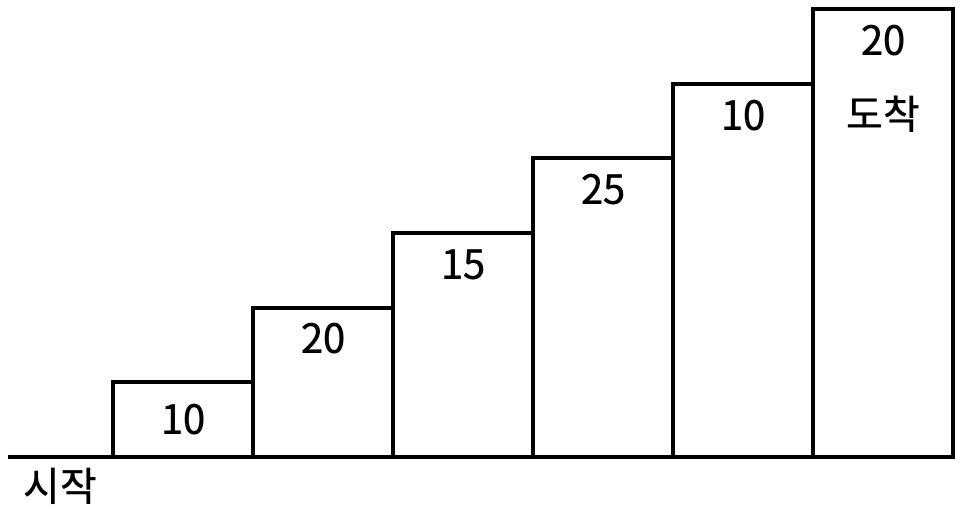
계단 오르는 데는 다음과 같은 규칙이 있다.
- 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
- 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
- 마지막 도착 계단은 반드시 밟아야 한다.
입력 & 출력
-
입력: 입력의 첫째 줄에 계단의 개수가 주어진다. 둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다. 계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.
-
출력: 첫째 줄에 계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력한다.
풀이
나의 생각
: 우선 위에서 내려오는 방식을 생각했다. 맨 위의 계단을 밟아야한다면 그 쪽이 편하리라 생각했다. 그러나 아직 DP를 명확하게 이해하지 못했던 것 같다. 자신이 밟고 있는 계단으로 올라오는 값을 계산하려면 이전의 값을 사용해야하는데 그부분을 고려하지 않았다. 또한 점화식을 생각하는 방법을 떠올리지 못해서 아쉽다.
참고 후 풀이
N번째 계단으로 오르기 위해서는 두가지의 방법이 존재한다.
1. N-3번 계단을 밟고 N-1번 계단을 밟은 후 오르는 방법
2. N-2번 계단을 밟고 오르는 경우
여기서 살짝 이해를 못했던 경우가 N-3>N-2>N 으로 오르는 순서를 생각했었는데 이 경우에도 N-2로 오르는 경우의 값을 이미 계산해두어 사용하기 때문에 위의 두 경우만 판별하면 된다는 것을 이해했다.
import sys
N = int(sys.stdin.readline())
answer = [0 for _ in range(N+1)]
stairs = [0]
for _ in range(N):
stairs.append(int(sys.stdin.readline()))
for i,v in enumerate(stairs):
if i==0:
pass
elif i == 1:
answer[i] = v
elif i == 2:
answer[i] = answer[i-1]+v
elif i == 3:
answer[i] = max(stairs[1]+v,stairs[2]+v)
else:
answer[i] = max(answer[i-3]+stairs[i-1]+v,answer[i-2]+v)
print(answer[N])느낀점 및 참고
느낀점
: 알고리즘 문제풀이에 시간 투자가 조금 더 필요할 것 같다. DP를 하면서 점화식 찾는 것이 생각보다 어렵다.
참고 문헌
백준 2579번 계단오르기 : https://v3.leedo.me/devs/64