(Binary, Easy) Counting Bits

https://leetcode.com/problems/counting-bits/description/

문제에서 O(n log n)으로 풀면 쉽지만 O(n) 시간으로 풀 수 있는지 묻고 있다.

O(n log n)으로 푸는 방식은
0 ~ n 까지 수행 * 각 순회마다 비트수 계산이다.

비트 수 계산은 Number of 1 Bits 문제에서 사용한 것과 같이 AND연산을 통해 하는 방식인 것 같다.

그런데 O(n)으로는 어떻게 풀 수 있을까?
힌트를 좀 얻어보니 이진수의 특성을 이용한 DP를 할 수 있다고 한다.

i에서 2를 나누거나 아니면 오른쪽으로 한 번 시프트한 것은 가장 오른쪽 비트(LSB, Least Significant Bit)를 사라지게 한다.

그렇다면 i >> 2하면 이진수 자릿수가 올라가기 전의 bitcount를 계산할 수 있고,
i % 2를 계산해서 더해주면 오른쪽 끝 비트가 1일지 0일지 계산할 수 있다 - 홀수는 항상 1이고, 짝수는 항상 0이다.

그럼 점화식은 아래 둘 중 하나로 구성할 수 있겠다.

dp[i] = dp[i/2] + (i % 2);
dp[i] = dp[i >> 1] + (i % 2);

이렇게 하면 O(n) 시간복잡도로 문제를 해결할 수 있다.

class Solution {
    public int[] countBits(int n) {
        
        int[] dp = new int[n+1];

        for (int i=1; i<=n; i++) {
            dp[i] = dp[i >> 1] + (i % 2);
        }

        return dp;
    }
}

솔루션을 참고해보면 다른 방식으로 2진수의 특성을 활용한 사례를 볼 수 있는데,
2의 제곱 단위로 자릿수가 커진다는 것을 기반으로 자릿수가 바뀔때마다 0, 그 이후 1씩 증가하여 비트카운트 계산하는 방식이 있다.

class Solution {
    public int[] countBits(int n) {
        int[] dp = new int[n + 1];
        int sub = 1;

        for (int i = 1; i <= n; i++) {
            if (sub * 2 == i) {
                sub = i;
            }

            dp[i] = dp[i - sub] + 1;
        }

        return dp;        
    }
}

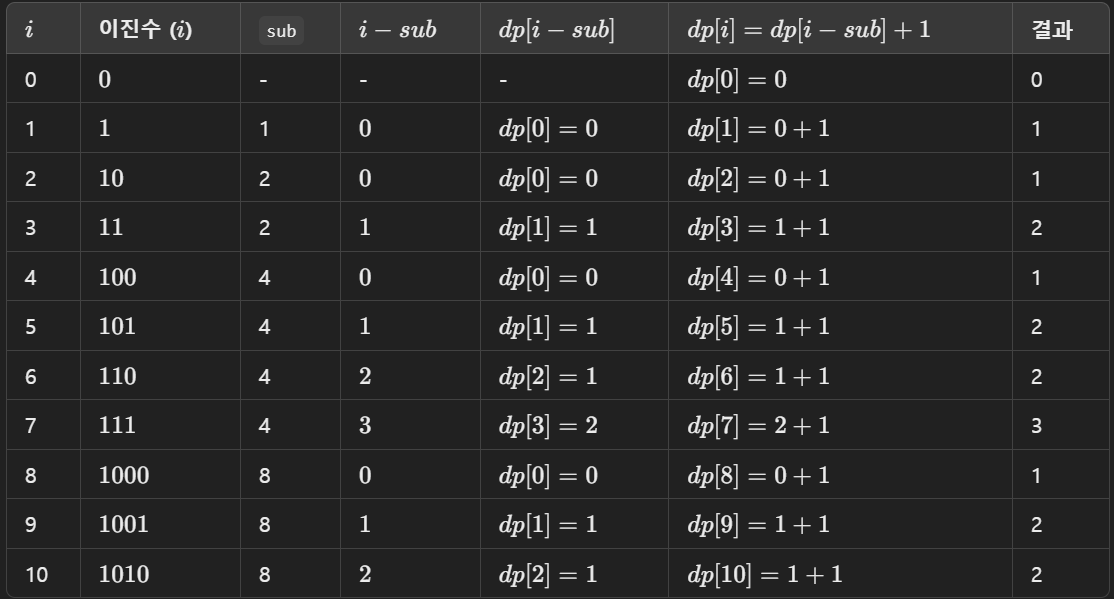
n=10일 때 계산 과정을 이미지로 보면 다음과 같다.